HDU 4312 Contest 2

题目要求两点间的最大值作为距离即：

 

即是切比雪夫距离。而切比雪夫距离与曼哈顿距离的转换却很巧妙。

把平面坐标所有点绕原点逆向旋转45度后，所得点的曼哈顿距离之和除以√2，即是切雪比夫距离。旋转点的公式是

 

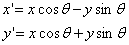
提取无理数，即每个新坐标可以是(x-y,x+y)。计算其曼哈顿距离后除以2即可。

 

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#define LL __int64
using namespace std;

struct point{
    int x,y;
    int num;
}acm[100005];
int n;

bool cmpx(point a, point b){
    if(a.x<b.x) return true;
    return false;
}
bool cmpy(point a,point b){
    if(a.y<b.y) return true;
    return false;
}

LL distx[100005],disty[100005];

LL mint(LL a,LL b){
    if(a<b) return a;
    return b;
}

void init(){
    for(int i=0;i<n;i++)
    distx[i]=disty[i]=0;
}

int main(){
    int T,a,b;
    scanf("%d",&T);
    while(T--){
        scanf("%d",&n);
        init();
        for(int i=0;i<n;i++){
            scanf("%d%d",&a,&b);
            acm[i].x=a-b; acm[i].y=a+b;
            acm[i].num=i;
        }
        LL tmp;
        sort(acm,acm+n,cmpx);
        tmp=0;
        for(int i=0;i<n;i++){
            if(!i)
                tmp=distx[acm[i].num]=0;
            else{
                distx[acm[i].num]=tmp=tmp+(LL)i*((LL)acm[i].x-(LL)acm[i-1].x);
            }
        }
        tmp=0;
        for(int i=n-1;i>=0;i--){
            if(i==n-1){
                tmp=0;
                distx[acm[i].num]+=tmp;
            }
            else {
                tmp=tmp+(LL)(n-1-i)*((LL)acm[i+1].x-(LL)acm[i].x);
                distx[acm[i].num]+=tmp;
            }
        }
        sort(acm,acm+n,cmpy);
        for(int i=0;i<n;i++){
            if(!i)
            disty[acm[i].num]=tmp=0;
            else{
                disty[acm[i].num]=tmp=tmp+(LL)i*((LL)acm[i].y-(LL)acm[i-1].y);
            }
        }
        for(int i=n-1;i>=0;i--){
            if(i==n-1){
                tmp=0;
                disty[acm[i].num]+=tmp;
            }
            else {
                tmp=tmp+(LL)(n-1-i)*((LL)acm[i+1].y-(LL)acm[i].y);
                disty[acm[i].num]+=tmp;
            }
        }
        LL ans=distx[0]+disty[0];
        for(int i=1;i<n;i++)
        ans=mint(ans,distx[i]+disty[i]);
        printf("%I64d\n",ans/2);
    }
    return 0;
}