HDU 1133

n+m个人排队买票，并且满足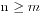，票价为50元，其中n个人各手持一张50元钞票，m个人各手持一张100元钞票，除此之外大家身上没有任何其他的钱币，并且初始时候售票窗口没有钱，问有多少种排队的情况数能够让大家都买到票。

这个题目是Catalan数的变形，不考虑人与人的差异，如果m=n的话那么就是我们初始的Catalan数问题，也就是将手持50元的人看成是+1，手持100元的人看成是-1，任前k个数值的和都非负的序列数。

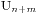这个题目区别就在于n>m的情况，此时我们仍然可以用原先的证明方法考虑，假设我们要的情况数是，无法让每个人都买到的情况数是，那么就有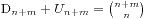，此时我们求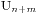，我们假设最早买不到票的人编号是k，他手持的是100元并且售票处没有钱，那么将前k个人的钱从50元变成100元，从100元变成50元，这时候就有n+1个人手持50元，m-1个手持100元的，所以就得到，于是我们的结果就因此得到了，表达式是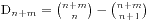

这个证明漂亮。http://daybreakcx.is-programmer.com/posts/17315.html

虽然知道卡特兰数一般证明方法，但这个题的变形我却不会证，唉，看来自己还差得远了。。。。

import java.math.BigDecimal;
import java.math.BigInteger;
import java.util.Scanner;
import java.io.InputStreamReader;

class Conmul{
    BigDecimal []m;
    Conmul(){
        m=new BigDecimal[101];
        m[0]=new BigDecimal(1);
        BigDecimal TMP;
        for(int i=1;i<=100;i++){
            TMP=new BigDecimal(i);
            m[i]=m[i-1].multiply(TMP);
        }
    }
}

class Choice{
  BigDecimal [][]C;
    Choice(){
        C=new BigDecimal[201][201];
	BigDecimal B,D;
	
        for(int i=0;i<=200;i++){
            for(int j=0;j<=200;j++){
                if(j==0)
                C[i][j]=new BigDecimal(1);
	else if(j>i) C[i][j]=new BigDecimal(0);
                else{
	B=new BigDecimal(i-j+1);
	D=new BigDecimal(j);
                    C[i][j]=C[i][j-1].multiply(B);
	C[i][j]=C[i][j].divide(D);
                }
            }
        }
    }
}

public class Main{
    public static void main(String args[]){
        Scanner in=new Scanner(System.in);
        BigDecimal []Can=new BigDecimal[101];
        Can[0]=new BigDecimal(1);
        BigDecimal B,C,D;
        Conmul Con=new Conmul();
        Choice Cho=new Choice();
        for(int i=1;i<=100;i++){
            B=new BigDecimal(4*i-2);
            C=new BigDecimal(i+1);
            D=Can[i-1].multiply(B);
            Can[i]=D.divide(C);
        }
        int kase=0;
        while(in.hasNext()){    
            int n=in.nextInt();
            int m=in.nextInt();
            if(m==0&&n==0)
                break;
	kase++;
            System.out.println("Test #"+kase+":");
            if(m>n){
                System.out.println(0);
            }
            else if(m==n){
                BigDecimal ans=new BigDecimal(1);
                ans=Con.m[n].multiply(Con.m[m]);
                ans=ans.multiply(Can[m]);
                System.out.println(ans);
            }
            else{
                BigDecimal ans=new BigDecimal(1);
	ans=ans.multiply(Con.m[n]);
                ans=ans.multiply(Con.m[m]);
	B=Cho.C[n+m][n].subtract(Cho.C[n+m][n+1]);
	ans=ans.multiply(B);
                System.out.println(ans);
            }
        }
    }
}