阶梯博弈&POJ 1704

阶梯博弈：

 

 

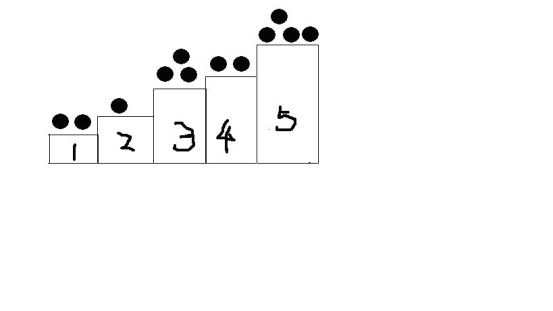
先借用别人的一幅图片。（1阶梯之前还有一个0阶梯未画出）

阶梯博弈的最初定义是这样的：每一个阶梯只能向它的前一个阶梯移动本阶梯的点，直至最后无法移动的为输。

那么，利用NIM，只计算奇数级的异或和，当为0时，先手必败。（至于为什么有这样的，我也能说明白，但下文要讨论的是怎么做）。

假设这样个NIM理解是对的。那么，要怎么移动呢？

首先（先手必胜情况下），先手必定移动奇数级的点到偶数级，使它的SG为0。对于后手，若他移动奇数级的点到偶数，则此时SG不为0，先手只需移动其他奇数级的点，即可使SG再为0。若后手移动偶数级的点到奇数，则先手只需把同等的点从该奇数级移走即可。

这个就是最基本的阶梯博弈。

 

 

POJ 1704

我们把每个CHESS当前可以移动的步数设为阶梯上的点，于是，把阶梯级数编号。注意，这里是从右往左编号，每次奇数级向前移动K步，则相当于把相应的点数移动到其右边的偶数级上。对偶数级移动也相同。于是，就是普通阶梯博弈了。

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;

int n;
int p[1010];
int stair[1010];

int main(){
    int cas;
    scanf("%d",&cas);
    stair[0]=0;
    while(cas--){
        scanf("%d",&n);
        p[0]=0;
        for(int i=1;i<=n;i++){
            scanf("%d",&p[i]);
        }
        sort(p,p+n+1);
        for(int i=1;i<=n;i++)
        stair[i]=p[i]-p[i-1]-1;
        int sum=0; int cnt=0;
        for(int i=n;i>=1;i--){
            cnt++;
            if(cnt&1)
            sum^=(stair[i]);
        }
        if(sum) printf("Georgia will win\n");
        else printf("Bob will win\n");
    }
    return 0;
}