2024.4.10 AVX2中permute函数补充说明 // OpenMP和MPI编程(积分求PI) // web框架介绍 // bash编程介绍 // gcc编译选项(优化基础)

permute函数(avx2指令集)

在AVX2中，permute函数用于重新排列输入向量中的元素。这可以用于整数和浮点数向量。具体的permute函数根据操作数的类型（如整数或浮点数）和指令的具体形式（如_mm256_permutevar8x32_epi32，_mm256_permute_ps等）而有所不同。

对于整数，一个常见的permute函数是_mm256_permutevar8x32_epi32，它允许根据第二个操作数（索引向量）中的索引重新排列第一个操作数（源向量）中的32位整数元素。

#include <immintrin.h>

int main() {
    __m256i src = _mm256_setr_epi32(1, 2, 3, 4, 5, 6, 7, 8); // 源向量
    __m256i indices = _mm256_setr_epi32(7, 6, 5, 4, 3, 2, 1, 0); // 索引向量
    __m256i result = _mm256_permutevar8x32_epi32(src, indices); // 根据索引重排源向量

    // 结果中的元素将是源向量的逆序: 8, 7, 6, 5, 4, 3, 2, 1
}

整数的重排列比较简单，难理解的是浮点数排列中的imm立即数的索引。
对于浮点数，可以使用_mm256_permute_ps函数，这允许你根据一个8位立即数（编译时常数）重新排列一个包含8个单精度浮点数的向量。

#include <immintrin.h>

int main() {
    __m256 src = _mm256_setr_ps(1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0); // 源向量
    __m256 result = _mm256_permute_ps(src, 0b01001110); // 重新排列向量

    // 结果将根据立即数索引重排: 3.0, 4.0, 1.0, 2.0, 7.0, 8.0, 5.0, 6.0
}

立即数索引规则：

在 _mm256_permute_ps 函数中，每两位二进制数对应于源向量 src 中的一个元素，从右到左。这里 00 代表 src 中的第一个元素（1.0），01 代表第二个元素（2.0），依此类推。
立即数 0b01001110 的二进制表示为：以右边为开始，每两位为一个单位

7th	6th	5th	4th	3rd	2nd	1st	0th
0	1	0	0	1	1	1	0

将每两位作为索引，我们得到：

索引	二进制	结果元素
0	00	1.0
1	01	2.0
2	10	3.0
3	11	4.0

因此，二进制立即数 0b01001110 按照上表中的索引定义了新的排列顺序。从右到左，每两位定义新向量中的一个元素，原来的顺序 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0 将会被重新排列为 3.0, 4.0, 1.0, 2.0, 7.0, 8.0, 5.0, 6.0。

OpenMP和MPI编程

OpenMP主要是在单机上进行并行，是基于共享内存的，共享内存就是多个核（包括单CPU多核和多CPU多核（都是单机））共享一个内存，只要是单台计算机都可以认为是共享内存，MP代表多线程的意思（Multi-Processing），其无法进行跨节点运算，并且OpenMP的库是默认集成在g++或者gcc里的；OpenMP在底层实现会链接Pthread库。
MPI则是用来进行多处理器，跨节点并行，OpenMPI是基于分布式内存，对于多台计算机组成的集群就是属于分布式内存。其中MPI是消息传递接口的意思（Message Passing Interface），OpenMPI也可以在单机上进行运行，但是由于其不同的核心之间的数据不是共享的，需要进行通信，因此速度不如OpenMP，常见的并行化策略是，在跨节点上采用OpenMPI编程,而在每个计算节点上采用OpenMP编程。

补一个vscode中格式化快捷键：

windows中,vscode格式化代码快捷键是“shift+alt+f”;
在mac中,vscode格式化代码快捷键是“shift+option+f”;
在ubuntu中,vscode格式化代码快捷键是“ctrl+shift+I”

通常来说，安装gcc以后就不需要再单独安装OpenMP了。可以用一个例子来检查是否可以执行OpenMP程序：

#ifdef _OPENMP
#include <omp.h>
#endif

#include <stdio.h>
#include "omp.h"
int main()
{
#if _OPENMP
    printf("hello world");
#endif
    return 0;
}

编译命令：
g++ -fopenmp first.cpp -o first.exe

也可以创建一个 bash 脚本，然后用比较简短的命令运行

bash 脚本名：omp.sh， 里面写：

g++ -fopenmp start.cpp -o start.exe
./start.exe

只需要以下命令一键运行：

bash omp.sh

以积分求PI的例子进行OpenMP的学习

计算PI

c/c++中计算PI：https://blog.csdn.net/wangnaisheng/article/details/135867160
c中利用公式计算PI：https://blog.csdn.net/AN_drew/article/details/131340999

利用莱布尼茨公式积分计算PI：

\(\pi = arccos(-1) = 2arcsin(1) = 4arctan(1)\)

\(\pi = 4 \int_0^1 \frac{1}{1 + x^2} \, dx\)
有：

double x, pi, sum = 0.0;   
  // 定义积分步长和步数
  int num_steps=1000000;
  double step = 1.0 / (double)num_steps;   
  // 积分求高度
  for (int i = 0; i< num_steps; i++)
  {      
   x = (i + 0.5)*step;      
   sum = sum + 4.0 / (1.0 + x*x);  
  }   
  // 求面积/积分
  pi = step * sum;

OpenMP下计算PI

分析：

#include <stdio.h>：包含标准输入输出库，用于执行I/O操作，例如printf。
#include <omp.h>：包含OpenMP库，这个头文件是必须的，以便使用OpenMP的功能。
static long num_steps = 100000000;：定义了一个静态长整型变量num_steps，设置为1亿，这个变量表示分割的矩形数量，也即迭代次数。
double step;：定义一个双精度浮点变量step，它将用于存储每个矩形的宽度。
int main()：主函数的开始。
int i;：定义一个整型变量i用于循环迭代。
double x, pi, sum = 0.0;：定义三个双精度浮点变量，x用于计算中间结果，pi用于存储计算出的π值，sum初始化为0，用于累加每个矩形的面积。
step = 1.0 / (double)num_steps;：计算每个矩形的宽度，即(1 / num_steps)。
#pragma omp parallel for reduction(+:sum) private(x)：这是一个OpenMP指令，用于并行化随后的for循环。
reduction(+:sum)：这是一个归约子句，它指示OpenMP为每个线程创建sum的本地副本，并在所有线程完成它们的计算后，将这些本地副本的值相加，更新到原始的sum变量中。
private(x)：这是一个私有子句，它指示每个线程应有其自己的x变量副本，防止不同线程间的数据竞争。
for (i = 0; i < num_steps; i++)：一个循环，从0开始到num_steps，每次迭代都会计算函数的一个矩形区域面积并累加到sum。
x = (i + 0.5) * step;：计算当前矩形的中点的x值。
sum += 4.0 / (1.0 + x*x);：计算当前矩形的面积（根据π的积分公式），并累加到sum。
pi = step * sum;：所有矩形的面积加起来乘以宽度，得到对π的估计值。
printf("pi = %f\n", pi);：输出计算得到的π的值。
return 0;：主函数返回。
整个程序是一个并行化的数值积分计算，用于估算π的值。通过将计算任务分散到多个处理器核心，OpenMP能够显著提高计算的速度。这个特定的计算利用了Leibniz公式来估算π的值，该公式定义了π/4与一个无穷级数的关系。在这个程序中，积分区间是[0,1]，并且函数是4/(1+x^2)。

程序中利用reducion归约子句，当所有线程完成它们的计算后，将这些本地副本的值相加，更新到原始的sum变量中。避免了手动累加sum/pi的过程；
且loop循环代码并行，也就是work sharing循环。loop是新的用词，等价于较老的for，实现了openmp的自动并行化，避免了手动配置线程的并行。

在OpenMP伪共享下计算PI

#include <stdio.h>
// OpenMP的库函数
#include <omp.h>

#define NTHREADS 4
static long long int num_steps = 1024 * 1024 * 1024;
double step = 0.0;
int main()
{
    int i, j, actual_nthreads;
    double pi, start_time, run_time;
    double sum[NTHREADS] = {0.0};
    step = 1.0 / (double)num_steps;
    omp_set_num_threads(NTHREADS);
    // 获取并行区域开始前的时间
    start_time = omp_get_wtime();
#pragma omp parallel
    {
        long long int i = 0;
        // 运行时函数获取当前线程id以及线程总个数
        int id = omp_get_thread_num();
        int numthreads = omp_get_num_threads();
        double x = 0.0;
        if (id == 0)
        {
            actual_nthreads = numthreads;
        }
        // 将线程总数打包循环
        for (i = id; i < num_steps; i += numthreads)
        {
            x = (i + 0.5) * step;
            sum[id] += 4.0 / (1.0 + x * x);
        }
    }
    pi = 0.0;
    // 回加sum到pi
    for (int ii = 0; ii < actual_nthreads; ii++)
    {
        pi += sum[ii];
    }
    pi = step * pi;
    run_time = omp_get_wtime() - start_time;
printf("\n pi is %f in %f seconds %d thrds \
\n",pi,run_time,actual_nthreads);
return 0;
}

程序中关键点介绍：
parallel子句：构造创建线程组执行区域的代码

但在伪共享程序中可以发现，每次线程进行取sum[i]的时候都是将整个cache行取到内存中，而这样则会造成伪共享的情况：

伪共享是多线程程序中的一种性能问题。当两个或多个线程访问同一缓存行的不同数据时，如果其中一个线程对其数据进行了修改，会导致其他线程中的数据无效。即使这些线程访问的数据是彼此独立的变量，只要它们位于同一缓存行中，一个线程的写操作都会使整个缓存行失效。这会迫使其他线程重新从主内存中加载这些数据，即使它们只是读取并没有修改数据。

于是将数组sum设计为一个二维数组，其第二维的大小是8。这是一个常用的避免伪共享的技巧，因为大多数现代系统的缓存行大小是64字节，而 double 类型通常是8字节。因此，每个 sum[id][0] 实际上占据一个缓存行，避免了多个线程访问相邻数据的情况。

解决伪共享后计算PI

#include <stdio.h>
#include <omp.h>

#define NTHREADS 4
static long long int num_steps = 1024 * 1024 * 1024;
double step = 0.0;
int main()
{
    int i, j, actual_nthreads;
    double pi, start_time, run_time;
    double sum[NTHREADS][8] = {0.0};
    step = 1.0 / (double)num_steps;
    omp_set_num_threads(NTHREADS);
    start_time = omp_get_wtime();
#pragma omp parallel
    {
        long long int i = 0;
        int id = omp_get_thread_num();
        int numthreads = omp_get_num_threads();
        double x = 0.0;
        if (id == 0)
        {
            actual_nthreads = numthreads;
        }
        for (i = id; i < num_steps; i += numthreads)
        {
            x = (i + 0.5) * step;
            sum[id][0] += 4.0 / (1.0 + x * x);
        }
    } // 隐式屏障(barrier).
    // 并行结束
    pi = 0.0;
    for (int ii = 0; ii < actual_nthreads; ii++)
    {
        pi += sum[ii][0];
    }
    pi = step * pi;
    run_time = omp_get_wtime() - start_time;
printf("\n pi is %f in %f seconds %d thrds \
\n",pi,run_time,actual_nthreads);
return 0;
}

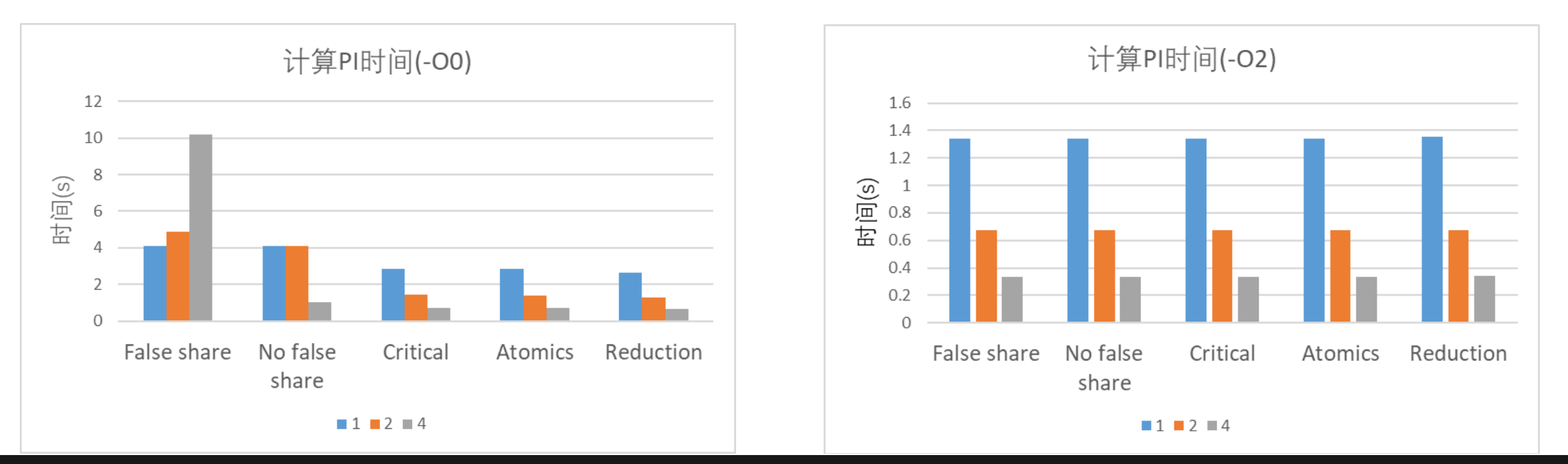
解决伪共享前后对比：

原子操作与临界区

临界区：

#pragma omp parallel
{
int id = omp_get_thread_num();
int numthreads = omp_get_num_threads();
double x, partial_sum = 0;
if (id == 0)
nthreads = numthreads;
for (long long int i = id; i < num_steps; i += 
numthreads) {
x = (i + 0.5) * step;
partial_sum += 4.0 / (1.0 + x * x);
}
#pragma omp critical
// 由于规定了临界区，每一时刻只能有一个线程对full_sum实现累加操作
full_sum += partial_sum;
}

原子操作：

#pragma omp parallel
{
int id = omp_get_thread_num();
int numthreads = omp_get_num_threads();
double x, partial_sum = 0;
if (id == 0)
nthreads = numthreads;
for (long long int i = id; i < num_steps; i += 
numthreads) {
x = (i + 0.5) * step;
partial_sum += 4.0 / (1.0 + x * x);
}
#pragma omp atomics
// 使用原子操作，使得累加操作安全，不会发生数据竞争。
full_sum += partial_sum;
}

计算素数(静态/动态调度)

#include <math.h>
#include <stdio.h>
#include <stdbool.h>
#include <omp.h>
#define ITER 50000000
bool check_prime(int num)
{
    int i;
    for (i = 2; i <= sqrt(num); i++)
    {
        if (num % i == 0)
            return false;
    }
    return true;
}
int main()
{
    int sum = 0;
#pragma omp parallel
    {
        int i;
        int id = omp_get_thread_num();
        double tdata = omp_get_wtime();
// #pragma omp for reduction (+:sum) schedule(static)
#pragma omp for reduction(+ : sum) schedule(dynamic)
        for (i = 2; i <= ITER; i++)
        {
            if (check_prime(i))
                sum++;
        }
        tdata = omp_get_wtime() - tdata;
        if (id == 0) printf("Number of prime numbers is %d in %f sec \n", sum, tdata);
    }
    return 0;
}

可以看到随着数字的增大，dynamic调度可以将前边的线程再利用而比static调度更快。

对openmp中collapse子句的说明

#include <omp.h>
#include <stdio.h>

#define N 100
#define M 100

int main() {
    double A[N][M];
    // 初始化数组
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < M; j++) {
            A[i][j] = i + j;
        }
    }

    #pragma omp parallel for collapse(2)
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < M; j++) {
            A[i][j] = A[i][j] * 2.0; // 一个简单的操作，每个元素乘以2
        }
    }

    // 输出结果的简单验证
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < M; j++) {
            printf("A[%d][%d] = %f\n", i, j, A[i][j]);
        }
    }

    return 0;
}

collapse(2)子句使得两层循环并行化，OpenMP将这两个循环视为单一迭代空间，并在多个线程之间分配迭代。

今天OpenMP就到这里😁，明天看OpenMP的task

web框架介绍

mark一些常用的web框架

前端
HTML/CSS/JavaScript：这三种技术是任何Web项目的基础。HTML负责结构，CSS处理样式，JavaScript负责交互。
框架与库：
React.js：一个由Facebook开发的JavaScript库，用于构建用户界面。
Vue.js：一个轻量级的MVVM前端框架。
Angular：一个由Google支持的前端框架，用于开发单页应用程序（SPA）。
Svelte：一个较新的前端编译框架，允许使用更少的代码来构建快速的Web应用。

后端
Node.js：一个能够让JavaScript运行在服务器端的平台，适用于构建快速、可扩展的网络应用。
Express.js：一个灵活的Node.js Web应用框架，设计简单，易于扩展。
Python：一种易于学习的高级编程语言，广泛用于Web开发。
Django：一个高级的Python Web框架，鼓励快速开发和干净、实用的设计。
Flask：一个轻量级的Python Web框架，适合于小型项目和微服务。
Ruby：
Ruby on Rails：一个Ruby框架，采用MVC架构，适合快速开发复杂的Web应用。
PHP：
Laravel：一个用于Web应用的PHP框架，提供了丰富的功能，如用户认证、路由、会话管理等。
Symfony：一个PHP框架，适用于构建大型企业级应用。
Java：
Spring Boot：一个用于简化Spring应用开发的框架，让你可以更快地启动和运行应用。
Go：
Gin：一个Go（Golang）编写的Web框架，以其高性能和易用性而闻名。

全栈
一些技术栈既适用于前端也适用于后端，允许开发者使用同一种语言进行全栈开发。
MEAN/MERN：这两种技术栈都使用JavaScript/Node.js。
MEAN：MongoDB, Express, Angular, Node.js
MERN：MongoDB, Express, React, Node.js

数据库
Web项目还需要数据库来存储数据。根据需求，你可能会选择关系型数据库（如PostgreSQL, MySQL）或非关系型数据库（如MongoDB）。

bash编程

基本命令介绍：https://blog.csdn.net/weixin_44657888/article/details/129386365
bash入门tutorial：https://zhuanlan.zhihu.com/p/651804369

简单的进行程序执行时间分析的脚本程序

#!/bin/bash

# 编译程序
gcc -fopenmp -o test_false_share test_false_share.c
gcc -fopenmp -o test_no_false_share test_no_false_share.c
# ...编译其他测试程序

# 运行测试并收集数据
echo "False Share, No False Share, Critical, Atomics, Reduction" > results.csv
for i in {1..10}; do
    # 获取时间
    time1=$(./test_false_share)
    time2=$(./test_no_false_share)
    # ...运行其他测试并获取时间

    # 将结果写入CSV文件
    echo "${time1}, ${time2}, ..." >> results.csv
done

# 使用Python或R脚本来读取results.csv并生成图表

gcc编译选项

GCC（GNU Compiler Collection）提供了多种编译优化选项，这些选项通过调整代码生成策略来改善程序的性能。常见的优化等级包括 -O0、-O1、-O2、-O3。

下面是一些编译器使用的关键技术和方法的简要说明（这些方法主要包括控制流分析、数据流分析、依赖分析等）：

1. 控制流分析（Control Flow Analysis）
   控制流分析的目的是确定程序中各部分代码的执行顺序。编译器构建一个所谓的控制流图（CFG），其中的节点表示程序中的指令块，边表示程序执行时可能的跳转路径。

死代码消除：通过控制流图，编译器可以发现那些从主程序流（如函数入口点）不可达的代码块。这些代码块称为死代码，因为在任何正常的程序执行路径中都不会执行到这些代码。
2. 数据流分析（Data Flow Analysis）
数据流分析用于收集关于程序中如何定义（写入）和使用（读取）变量的信息。通过这些信息，编译器可以进行如下优化：

常量传播：如果一个变量在被使用前已被赋予一个常量值，编译器可以直接在使用点替换该变量为其常量值。
无用指令删除：如果某个变量的值被计算出来但从未被使用，那么计算这个变量的操作可以被移除。
复制传播：如果变量b被赋值为另一个变量a的值，那么在不影响程序行为的情况下，直接使用a代替b可以减少变量数量和潜在的内存访问。
3. 依赖分析（Dependency Analysis）
依赖分析帮助编译器理解不同数据和控制结构之间的依赖关系。这种分析对并行化代码尤为重要。

循环优化：编译器通过分析循环内部的数据依赖关系来应用循环展开、循环融合等技术，这可以显著提高循环的执行效率。
4. 副作用分析（Side-Effect Analysis）
在进行函数调用优化（如内联）时，理解函数可能产生的副作用（如修改全局变量、执行I/O操作）是非常重要的。

函数内联：如果一个函数没有副作用，或者其副作用在特定上下文中可控，则可以将函数内联到调用点，以减少函数调用的开销。
5. 抽象解释（Abstract Interpretation）
这是一种理论方法，用于在编译时估计程序在运行时的行为。它可以用来检测程序的可能状态，从而用于优化和提前错误检测。

范围检查优化：编译器可以通过抽象解释预测变量的可能范围，从而优化程序中的条件语句。
综合应用
通过这些方法的综合应用，编译器能够在不改变程序语义的前提下，对程序进行多方面的优化，包括提高运行速度、减少内存使用和磁盘空间占用等。正是因为有了这些高级的静态分析技术，现代编译器如GCC和Clang能够提供广泛的优化选项，帮助开发者最大化程序性能。

当优化标识被启用之后，gcc编译器将会试图改变程序的结构（当然会在保证变换之后的程序与源程序语义等价的前提之下），以满足某些目标。在不同的gcc配置和目标平台下，同一个标识所采用的优化种类也是不一样的，这可以使用-Q --help =optimizers来获取每个优化标识所启用的优化选项。

-O

-O1

提供合理的性能提升同时保持编译时间较短和较少的资源消耗。是GCC的基本优化级别。这个级别旨在提供编译过程中的最佳编译速度和合理的运行时性能。它尝试减少编译时间和执行时间之间的折衷，同时不会使用过多的编译资源。-O1 包括：简单的数据流分析；局部变量的寄存器分配；消除无用代码（如未执行的代码块）；简单的循环优化（如循环不变代码移出循环）。

这两个命令的效果是一样的，目的都是在不影响编译速度的前提下，尽量采用一些优化算法降低代码大小和可执行代码的运行速度。并开启如下的优化选项：

优化选项详解
通用优化

-fauto-inc-dec：优化自增和自减操作的代码生成。
-fbranch-count-reg：优化分支条件的计数器使用，减少寄存器使用。
-fcombine-stack-adjustments：合并多个对栈指针的调整操作为单一操作，减少代码量。
-fcompare-elim：消除某些比较操作，尤其是那些可以通过其他指令隐含的比较。
-fcprop-registers：在寄存器之间传播常数，以减少不必要的加载和存储。
数据流与死代码优化

-fdce（Dead Code Elimination）：移除不会被执行到的代码。
-fdse（Dead Store Elimination）：移除对变量的写操作，如果写入的值之后无被读取。
-fdefer-pop：优化堆栈操作，推迟弹栈操作以合并多个弹栈。
-fdelayed-branch：在分支指令后重新排序指令以改善CPU流水线效率。
循环和分支优化

-fforward-propagate：前向传播寄存器内容，减少不必要的数据传输。
-fguess-branch-probability：估计分支概率，用于更好的分支预测。
-fif-conversion、-fif-conversion2：将条件分支转换为条件移动等指令，减少分支。
函数调用和内联

-finline-functions-called-once：内联调用次数极少的函数，减少调用开销。
-fipa-pure-const：分析函数是否是纯函数或常数函数，这可以增强进一步的优化。
-fipa-profile：使用分析数据来指导内联等优化。
-fipa-reference：分析和优化函数间的引用传递。
常量和变量处理

-fmerge-constants：合并相同的常量数据，减少程序大小。
-fmove-loop-invariants：循环不变式外提，减少循环内部的计算量。
-ftree-bit-ccp、-ftree-ccp：传播条件常量。
-ftree-ch：循环启发式优化。
-ftree-coalesce-vars：合并变量以减少占用的寄存器数量。
-ftree-copy-prop：在树结构中进行复制传播。
-ftree-dce：在树优化阶段移除死代码。
-ftree-dominator-opts：应用支配树优化技术。
-ftree-dse：在树优化阶段进行死存储消除。
-ftree-forwprop：在树优化阶段进行前向传播优化。
-ftree-fre：执行完全冗余消除。
-ftree-phiprop、-ftree-pta、-ftree-ter：各种基于SSA形式的树优化。
其他优化

-fshrink-wrap、-fshrink-wrap-separate：优化函数的寄存器保存和恢复位置。
-fsplit-wide-types：拆分宽类型操作，优化64位整型等的处理。
-fssa-backprop、-fssa-phiopt：在SSA形式的代码上应用优化。
-fstore-merging：合并相邻的存储操作，减少内存操作次数。
-ftree-sink：优化变量位置，使其尽可能靠近使用位置。
-ftree-slsr：执行强度削减和重复代码合并。
-ftree-sra：对结构体进行标量替换。
-funit-at-a-time：在整个编译单元中进行优化，而不仅是单个函数。
这些优化选项都是为了提升程序的运行效率、减少程序的体积以及提高编译的有效性。不过，开启过多优化可能会增加编译时间和复杂性，有时候甚至可能引入难以预料的问题，所以应当根据具体情况和需求谨慎选择合适的优化级别和选项。

O2

在不过分牺牲编译时间的基础上提供较好的性能优化。-O2 提供了比 -O1 更深入的优化，它包括所有 -O1 的优化，并增加了一些可能显著增加编译时间的优化技术。这个级别着重于提升程序的执行速度而不是编译速度。-O2 包括：
所有 -O1 级别的优化
更高级的循环优化（例如循环展开、循环交换）
内联函数
延迟分支
预测分支
高级数据流分析

该优化选项会牺牲部分编译速度，除了执行-O1所执行的所有优化之外，还会采用几乎所有的目标配置支持的优化算法，用以提高目标代码的运行速度

跳转和分支优化
-fthread-jumps：优化条件跳转，将条件相似的跳转合并。
-fcrossjumping：交叉跳转优化，合并执行相似代码序列的不同分支。
-fcse-follow-jumps、-fcse-skip-blocks：在跳转后继续执行公共子表达式消除（CSE），即便是跳过某些代码块也要尝试执行。
对齐优化
-falign-functions：对齐函数的入口地址。
-falign-jumps：对齐跳转指令地址。
-falign-loops：对齐循环起始的地址。
-falign-labels：对齐标签地址，优化跳转指令的预测准确性和执行速度。
函数调用与加载优化
-fcaller-saves：优化通过在调用点保存和恢复寄存器来减少调用开销。
-fhoist-adjacent-loads：提升相邻的加载操作，减少重复加载。
-foptimize-sibling-calls：优化递归调用为尾调用，减少栈使用。
-foptimize-strlen：优化 strlen 函数的使用，通过内联展开等手段减少调用开销。
代码重组和内联优化
-finline-small-functions：内联小函数，减少函数调用的开销。
-findirect-inlining：间接内联，内联那些间接通过函数指针调用的函数。
-fpartial-inlining：部分内联，只内联函数的一部分以减少代码膨胀。
-freorder-functions：重排函数定义，优化调用的局部性，减少页面错误。
-fpeephole2：执行第二遍窥孔优化，移除冗余的机器指令。
路径隔离和错误处理
-fdelete-null-pointer-checks：删除对空指针的检查，假定指针不会是空。
-fisolate-erroneous-paths-dereference：隔离错误路径，对潜在的错误解引用进行特殊处理。
循环和调度优化
-fgcse、-fgcse-lm：全局公共子表达式消除和其循环版本的优化。
-frerun-cse-after-loop：在循环后重新运行CSE。
-fsched-interblock、-fsched-spec：跨块调度和投机性调度，优化指令的调度顺序以减少延迟。
-fschedule-insns、-fschedule-insns2：指令调度，尝试减少CPU流水线的停顿。
高级优化和内存访问
-fstrict-aliasing：允许编译器假设不同类型的指针不会别名，提高优化级别。
-fstrict-overflow：允许编译器优化可能导致溢出的运算。
-fcode-hoisting：提前代码，尝试将计算移动到使用前最早可能的地方。
-ftree-pre：部分冗余消除。
-ftree-vrp：值范围传播，分析并应用变量值的可能范围来优化代码。
面向对象和虚函数
-fdevirtualize、-fdevirtualize-speculatively：尝试将虚函数调用转换为直接调用，以减少虚拟机制的开销。
其他专门优化
-fipa-cp、-fipa-cp-alignment：常数传播和对齐，全程序分析的一部分。
-fipa-bit-cp、-fipa-sra：位域常数传播和标量替换聚合。
-fipa-icf：相同函数合并，减少代码大小。
-freorder-blocks-algorithm=stc、-freorder-blocks-and-partition：重排序基本块以优化跳转和缓存使用。

O3

最大化程序的执行速度，适用于对性能要求极高的应用。-O3 是GCC提供的最高优化级别，包括所有在 -O2 中提供的优化，并添加了更多专门的高级优化技术，旨在最大化程序的执行性能。不过，这些优化可能会导致编译时间大幅增加，并且有时候可能会导致生成的程序大小增加（代码膨胀）。-O3 包括：

所有 -O2 级别的优化
更积极的函数内联
更完整的循环优化，如循环融合
自动向量化，使用SIMD指令
更积极的指令调度等

该选项除了执行-O2所有的优化选项之外，一般都是采取很多向量化算法，提高代码的并行执行程度，利用现代CPU中的流水线，Cache等

函数内联和代码变换
-finline-functions：对所有合适的函数（即使它们没有显式标记为内联）应用启发式算法进行内联。这通常会增加执行速度，因为它减少了函数调用的开销，但可能会增加编译后的代码大小。
循环优化
-funswitch-loops：将循环中的条件判断移动到循环外部，如果循环内的条件不依赖于循环变量，这可以减少循环内的分支判断次数。
-fpredictive-commoning：在循环中，对计算进行优化，以便在多个迭代中重用之前的计算结果。
-fgcse-after-reload：在寄存器重分配后执行全局共同子表达式消除，进一步减少不必要的计算和提高代码效率。
-ftree-loop-vectorize：自动将循环向量化以利用SIMD指令，这可以显著提高数据处理的速度。
-ftree-loop-distribute-patterns：识别并转换特定的循环模式，比如数组的零初始化，将其转化为更高效的库调用或者优化的代码路径。
-fsplit-paths：在复杂的控制流中分割代码路径，以提高特定路径的优化程度和执行速度。
-fpeel-loops：对循环进行剥离，将循环的某些迭代单独处理，用于减少边界检查或者改进向量化。
向量化和并行处理
-ftree-slp-vectorize：执行超级字长包（SLP）向量化，将多个独立的标量操作组合成单个向量操作，以利用向量处理单元。
-fvect-cost-model：启用向量化成本模型，评估向量化的成本与收益，决定是否进行向量化。
-ftree-partial-pre：执行部分冗余消除（PRE），优化在多个路径上重复的计算。
函数克隆和专门化
-fipa-cp-clone：对于那些参数非常相似的函数调用，通过克階创建特定版本以提高效率。这使得编译器可以为特定的使用情况定制函数体。

其他编译优化选项：

-Os：在优化代码执行速度的同时，减少编译后的代码大小。这个优化标识和-O3有异曲同工之妙，当然两者的目标不一样，-O3的目标是宁愿增加目标代码的大小，也要拼命的提高运行速度，但是这个选项是在-O2的基础之上，尽量的降低目标代码的大小，这对于存储容量很小的设备来说非常重要。为了降低目标代码大小，会禁用压缩内存中的对齐空白(alignment padding)等优化选项。
-Ofast：不考虑标准的严格性，追求尽可能高的性能。无视严格的标准合规性。-Ofast启用所有-O3优化。它还支持不适用于所有符合标准的程序的优化。它打开-ffast-math、-fallow-store-data-races和Fortran特定的-fstack-arrays，除非指定了-fmax-stack-var-size和-fno-protect-parens。它关闭了-fsemantic-interposition。

gcc文档：https://gcc.gnu.org/onlinedocs/gcc/Optimize-Options.html
GCC中-O1 -O2 -O3 优化的区别是什么？https://blog.csdn.net/liang_baikai/article/details/110137374

参考资料：
c语言中怎么求积分：https://www.kdun.com/ask/417908.html
MATLAB编程计算圆周率：https://zhuanlan.zhihu.com/p/446051972
OpenMP入门：https://zhuanlan.zhihu.com/p/658770855
国科大-高性能计算编程-课件

分享一个用c写的llms：

前特斯拉AI主管、OpenAI联合创始人安德烈·卡帕西在github上上线了开源项目llm.c，纯粹使用C语言来训练大型语言模型（LLMs）。该项目仅用大约1,000行清晰的代码实现了在CPU/fp32上训练GPT-2的功能。它能够立即编译和运行，并且与PyTorch的参考实现完全匹配。这个项目对于想学习大模型底层原理的人很有帮助。
https://github.com/karpathy/llm.c
好文杂文分享：
秋招看到github上不错的项目，但不知道该咋学？https://ost.51cto.com/posts/18352
如何参与开源项目 - 细说 GitHub 上的 PR 全过程：https://www.cnblogs.com/daniel-hutao/p/open-a-pr-in-github.html
一份百投百中的计算机校招简历是如何迭代足足26版的？https://mp.weixin.qq.com/s?__biz=Mzk0ODU4MzEzMw==&mid=2247511499&idx=1&sn=ba8f76bd3295e175d0b6f9b40273c1a9&source=41#wechat_redirect
左值引用、右值引用、移动语义、完美转发，你知道的不知道的都在：https://ost.51cto.com/posts/274
从线程概念到linux多线程的所有知识点，一网打尽：https://mp.weixin.qq.com/s/bB4yBd7nPD7ezgJY6Y1kJA