$用python玩点有趣的数据分析——一元线性回归分析实例
本文参考了博乐在线的这篇文章,在其基础上加了一些自己的理解。其原文是一篇英文的博客,讲的通俗易懂。
本文通过一个简单的例子:预测房价,来探讨怎么用python做一元线性回归分析。
1. 预测一下房价
房价是一个很火的话题,现在我们拿到一组数据,是房子的大小(平方英尺)和房价(美元)之间的对应关系,见下表(csv数据文件):
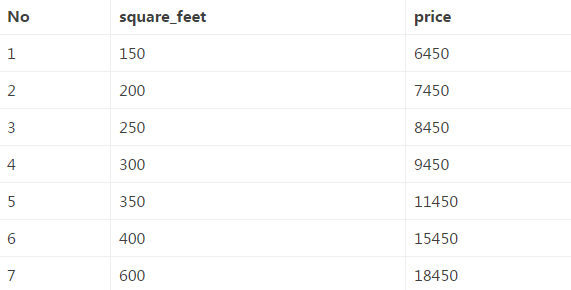
从中可以大致看出,房价和房子大小之间是有相关关系的,且可以大致看出来是线性相关关系。为了简单起见,这里理想化地假设房价只和房子大小有关,那我们在这组数据的基础上,怎样预测任意大小的房子的房价呢?答案是用一元回归分析。
2. 一元回归分析是啥
讲到一元回归分析很多人应该不陌生,在初中还是高中的数学课程中肯定有学过,即对于一组自变量x和对应的一组因变量y的值,x和y呈线性相关关系,现在让你求出这个线性关系的直线方程,就是这样一个问题。
记得当时用的方法叫:最小二乘法,这里不再细讲最小二乘法的详细内容,其主要思想就是找到这样一条直线,使得所有已知点到这条直线的距离的和最短,那么这样一条直线理论上就应该是和实际数据拟合度最高的直线了。
下面我们将开篇提出的问题中的房价和房子的大小之间的关系用一个线性方程来表示:
表示大小为x(单位:平方英尺)的房子的价格为\(h_\theta(x)\),其中\(\theta_0\)是直线的截距,\(\theta_1\)为回归系数,即直线的斜率。
我们要计算的东西其实就是\(\theta_0\)和\(\theta_1\)这两个系数,因为只要这两个系数确定了,那直线的方程也就确定了,然后就可以把要预测的x值代入方程来求得对应的\(h_\theta\)值了。
3. 上代码
注:用到的3个库都可以用pip命令进行安装。
#!/usr/bin/python
# coding:utf-8
# python一元回归分析实例:预测房子价格
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.linear_model import LinearRegression
# 从csv文件中读取数据,分别为:X列表和对应的Y列表
def get_data(file_name):
# 1. 用pandas读取csv
data = pd.read_csv(file_name)
# 2. 构造X列表和Y列表
X_parameter = []
Y_parameter = []
for single_square_feet,single_price_value in zip(data['square_feet'],data['price']):
X_parameter.append([float(single_square_feet)])
Y_parameter.append(float(single_price_value))
return X_parameter,Y_parameter
# 线性回归分析,其中predict_square_feet为要预测的平方英尺数,函数返回对应的房价
def linear_model_main(X_parameter,Y_parameter,predict_square_feet):
# 1. 构造回归对象
regr = LinearRegression()
regr.fit(X_parameter,Y_parameter)
# 2. 获取预测值
predict_outcome = regr.predict(predict_square_feet)
# 3. 构造返回字典
predictions = {}
# 3.1 截距值
predictions['intercept'] = regr.intercept_
# 3.2 回归系数(斜率值)
predictions['coefficient'] = regr.coef_
# 3.3 预测值
predictions['predict_value'] = predict_outcome
return predictions
# 绘出图像
def show_linear_line(X_parameter,Y_parameter):
# 1. 构造回归对象
regr = LinearRegression()
regr.fit(X_parameter,Y_parameter)
# 2. 绘出已知数据散点图
plt.scatter(X_parameter,Y_parameter,color = 'blue')
# 3. 绘出预测直线
plt.plot(X_parameter,regr.predict(X_parameter),color = 'red',linewidth = 4)
plt.title('Predict the house price')
plt.xlabel('square feet')
plt.ylabel('price')
plt.show()
def main():
# 1. 读取数据
X,Y = get_data('./price_info.csv')
# 2. 获取预测值,在这里我们预测700平方英尺大小的房子的房价
predict_square_feet = 700
result = linear_model_main(X,Y,predict_square_feet)
for key,value in result.items():
print '{0}:{1}'.format(key,value)
# 3. 绘图
show_linear_line(X,Y)
if __name__ == '__main__':
main()
【输出结果】
coefficient:[ 28.77659574]
predict_value:[ 21915.42553191]
intercept:1771.80851064
4. 总结与不足
上述分析过程,有两点不足:
(1)数据量太少,预测的误差可能较大;
(2)影响房价不止房子大小这一个因素,肯定还有很多其他因素,这里没有把其他因素考虑进去,导致预测的结果也是不准确的。既然有一元回归分析,那肯定也有多元回归分析,留到以后再讲。
但是我们也看到可以用python的一些科学计算和数据分析的库自动的帮我们完成以前需要繁琐计算的过程,更加灵活高效,特别是面对上万上百万规模的数据的时候。



