核函数

几个常用的核函数：

​ 根据问题和数据的不同，选择不同的参数，实际上就是得到了不同的核函数。

1.多项式核

​ \(K(x,z) = (x \bullet z + 1)^p\)，在此情形下，分类决策函数成为：

​ \(f(x) = \mbox{sign}(\sum_{i=1}^{N_s}a_i^*y_i(x_i\bullet x + 1)^p + b^*)\)

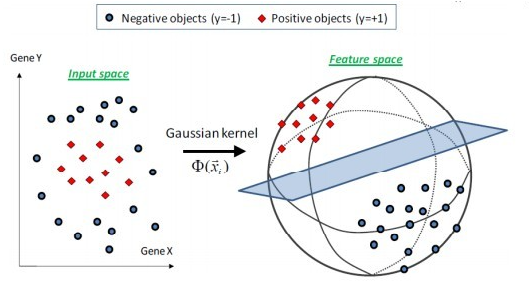
2.高斯核

​ \(K(x_1,x_2)=\exp{-\frac{||x_1-s_2||^2}{2\sigma^2}}\)

​ 这个核就会将原始空间映射为无穷维空间。若\(\sigma\)选的很大，高次特征上的权重实际上衰减的非常快，所以实际上相当于一个低维的子空间；若\(\sigma\)选的很小，则可以将任意的数据映射为线性可分，但是可能会导致严重过拟合。

​ 总的来说，通过调控参数\(\sigma\)，高斯核有相当高的灵活性，也是使用最广泛的核函数之一。

3.线性核

​ \(K(x_1,x_2)=\langle x_1,x_2 \rangle\),这实际上就是原始空间的内积。这个核存在的主要目的是使得“映射后空间中的问题”和“映射前空间中的问题”两者在形式上统一起来。

核函数的本质

1. 实际中，我们会经常遇到线性不可分的样例，此时，我们的常用做法是把样例特征映射到高维空间中去
2. 但进一步，如果凡是遇到线性不可分的样例，一律映射到高维空间，那么这个维度大小是会高到可怕的(如上文中19维乃至无穷维的例子)。那咋办呢？
3. 此时，核函数就隆重登场了，核函数的价值在于它虽然也是讲特征进行从低维到高维的转换，但核函数绝就绝在它事先在低维上进行计算，而将实质上的分类效果表现在了高维上，也就如上文所说的避免了直接在高维空间中的复杂计算。

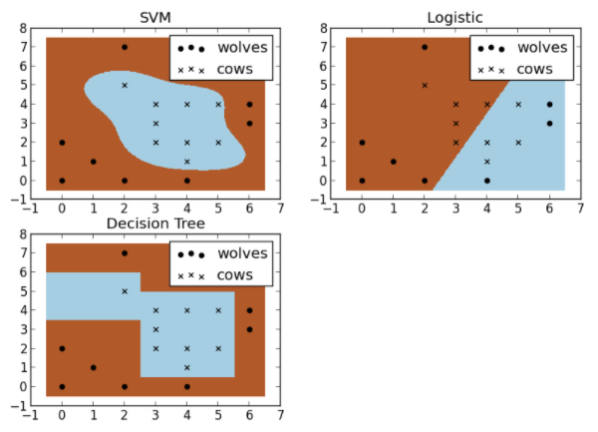
假设现在你是一个农场主，圈养了一批羊群，但为预防狼群袭击羊群，你需要搭建一个篱笆来把羊群围起来。但是篱笆应该建在哪里呢？你很可能需要依据牛群和狼群的位置建立一个“分类器”，比较下图这几种不同的分类器，我们可以看到SVM完成了一个很完美的解决方案。