线性回归与梯度下降法

• 一元线性回归

①基本假设： 　　　

y = w0 + w1x + ε 其中 w0,w1 为回归系数，ε 为随机误差项(noise)

给定样本集合 D = { (x1,y1),…,(xn,yn)}，

我们的目标是找到一条直线　y = w0 + w1x ，使得所有样本点尽可能落在它的附近，即求解以下问题：

 

 ②一元线性回归的参数估计：

 

 一元线性回归可以解出精确解。不需要求近似解。

 

• 多元线性回归

 

 

 

 

 

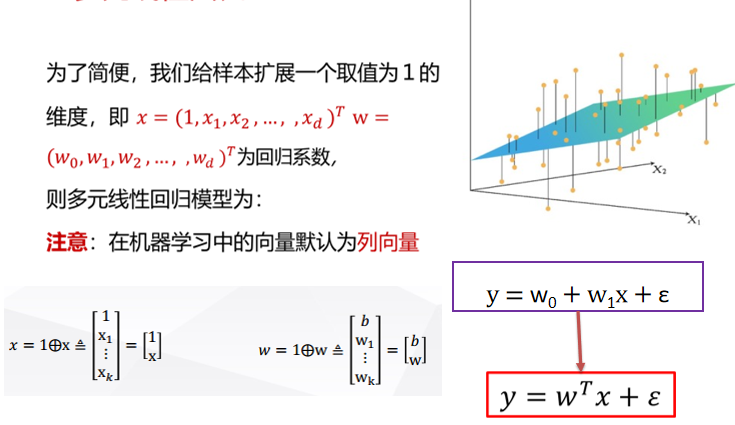
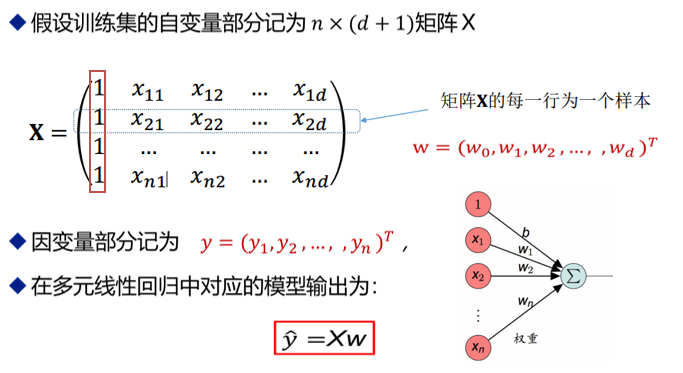
 注意，当不满秩时，就需要用梯度下降法来求近似解。

• 梯度下降法求解多元线性回归问题：