R 《回归分析与线性统计模型》page121,4.4

rm(list = ls())
A = read.xlsx("xiti_4.xlsx",sheet = 4)
names(A) = c("ord","x","y")

　　

#进行回归
attach(A)
fm = lm(y~x)
summary(fm)
coef(fm)

　　

#回归残差关于x的散点图
plot(x,resid(fm))

　　

 

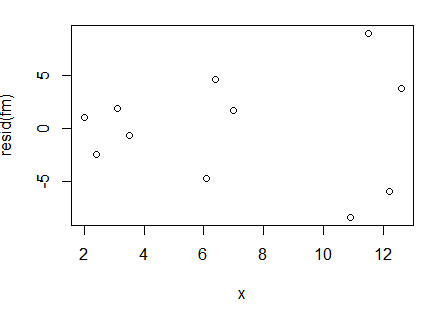
 成发射状，意味着方差随着x的增加而变大

#尝试用加权最小二乘
#先分类(可以聚类、手动分类)
plot(x)

　　

 

 根据变量x的图像，手动分为三类（1-4，5-7，8-11）

detach(A)

　　

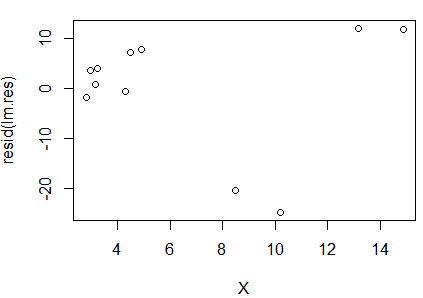
#计算权重
se = deviance(fm)/11 #权重的分母项
#S1
A1 = A[c(1:4),]
lm1 = lm(A1$y~A1$x)
sig1 = deviance(lm1)/lm1$df
csq1 = sig1/se      #第一类的权重
#S2
A2 = A[c(5:7),]
lm2 = lm(A2$y~A2$x)
sig2 = deviance(lm2)/lm2$df
csq2 = sig2/se      #第二类的权重
#S3
A3 = A[c(8:11),]
lm3 = lm(A3$y~A3$x)
sig3 = deviance(lm3)/lm3$df
csq3 = sig3/se      #第三类的权重

sig = c(sig1,sig2,sig3) #各类σ^2
csq = c(csq1,csq2,csq3) #权重向量

#加权最小二乘法分析
Y = c(A1$y/csq[1],A2$y/csq[2],A3$y/csq[3])
X = c(A1$x/csq[1],A2$x/csq[2],A3$x/csq[3])
lm.res = lm(Y~X)
summary(lm.res)
plot(X,resid(lm.res))