R WLS矫正方差非齐《回归分析与线性统计模型》page115

rm(list = ls())
A = read.csv("data115.csv")
fm = lm(y~x1+x2,data = A)
coef(fm)

A.cooks = cooks.distance(fm) #计算cook距离
new_A = cbind(A,A.cooks) #把原始数据与cook距离放在一个数据框中查看
new_A[order(A.cooks,decreasing = T),]#按cook距离降序排列

显示西藏地区数据对应的cook统计量明显过大，不能放入建模分析中

A = A[-26,] #剔除西藏数据
fm1 = lm(y~x1+x2,data = A)
summary(fm1)
anova(fm1) 

　

进行正态性检验、残差分析

par(mfrow=c(2,2))
e = resid(fm1)
d = e/sqrt(deviance(fm1)/27) #标准化残差
hist(d,probability = T)      #绘制回归标准化残差概率图
lines(density(d),col='red')  #添加回归线

qqnorm(d) #QQ图正态性检验
qqline(d) #添加趋势线

r = rstudent(fm1)
plot(A$y,r,ylim = c(-1,4),xlim = c(1000,6000)) #标准化残差关于响应变量图

　　

 

 显示存在异方差

利用WLS修正异方差

#利用WLS修正异方差
se = deviance(fm1)/30  #计算全模型的1/n残差平方和
#S1
A1 = A[A$jbh==1,]
lm1 = lm(y~x1+x2,data = A1)
sig1 = deviance(lm1)/lm1$df #σ^2的估计
csq1 = sig1/se              #WLS方法所需要的权重
#S2
A2 = A[A$jbh==2,]
lm2 = lm(y~x1+x2,data = A2)
sig2 = deviance(lm2)/lm2$df
csq2 = sig2/se
#S3
A3 = A[A$jbh==3,]
lm3 = lm(y~x1+x2,data = A3)
sig3 = deviance(lm3)/lm3$df
csq3 = sig3/se
#S4
A4 = A[A$jbh==4,]
lm4 = lm(y~x1+x2,data = A4)
sig4 = deviance(lm4)/lm4$df
csq4 = sig4/se

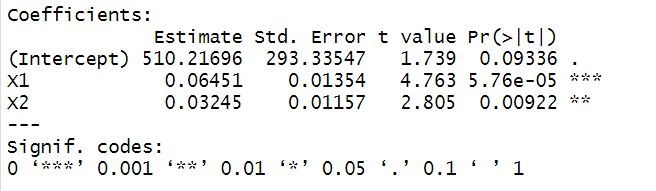
　　人均教育经费数据WLS估计结果：

#人均教育经费数据WLS估计结果
nj = c(nrow(A1),nrow(A2),nrow(A3),nrow(A4))
cj = c(csq1,csq2,csq3,csq4) #权重
#数据变换，除以相应的权重
Y = c(A1$y/cj[1],A2$y/cj[2],A3$y/cj[3],A4$y/cj[4])
X1 = c(A1$x1/cj[1],A2$x1/cj[2],A3$x1/cj[3],A4$x1/cj[4])
X2 = c(A1$x2/cj[1],A2$x2/cj[2],A3$x2/cj[3],A4$x2/cj[4])

lm_res = lm(Y~X1+X2)
summary(lm_res)

　　

 

 

#残差分析、正态性检验
par(mfrow=c(2,2))
e = resid(lm_res)
d = e/sqrt(deviance(lm_res)/27) #标准化残差
hist(d,probability = T)      #绘制回归标准化残差概率图
lines(density(d),col='red')  #添加回归线

qqnorm(d) #QQ图正态性检验
qqline(d) #添加趋势线

r = rstudent(lm_res)
plot(Y,r) #回归学生化残差-响应变量散点图