R语言 方差稳定化变换与线性变换 《回归分析与线性统计模型》page96

> rm(list = ls())
> A=read.csv("data96.csv")
> A
   Y      N
1 11 0.0950
2  7 0.1920
3  7 0.0750
4 19 0.2078
5  9 0.1382
6  4 0.0540
7  3 0.1292
8  1 0.0503
9  3 0.0629
> attach(A) #将数据A的列名直接赋为变量

　

plot(N,Y) #绘制散点图
lm.air=lm(Y~N) #线性回归
summary(lm.air)

 

 

 

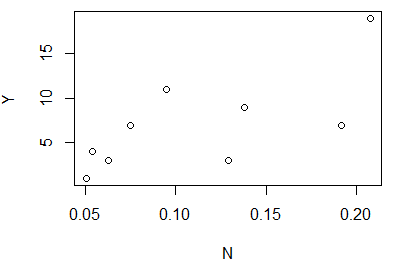
e.norm1=(e-mean(e))/sqrt((sum(e^2))/(n-2)) #计算标准化残差 //scale()函数将一组数据进行中心化、标准化 但是我觉得不能用于求标准化残差
plot(Y,e.norm1,ylab = "标准化残差") #绘制标准化残差关于响应变量Y的散点图

　　

 

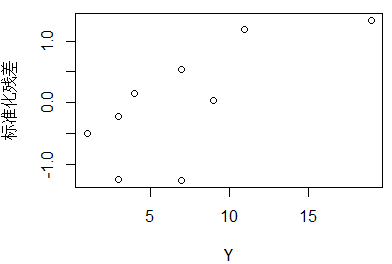
 从这个图看出残差随着N的增大而增大，因此似乎违背了方差齐性的假定。因为损害事故数可能是一个泊松分布，其方差与均值成比例。

由于可能是泊松分布，泊松分布的方差与均值有一次比例关系，所以为了保证方差齐性假定，我们做平方根变换。

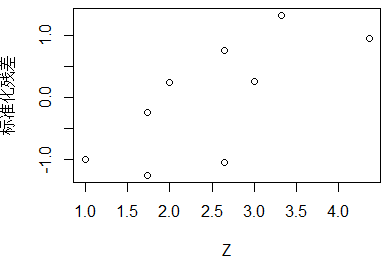
Z=sqrt(Y) 
plot(N,Z) #绘制散点图
lm.air1=lm(Z~N) #线性回归
summary(lm.air1)

e1=lm.air1$resid
e.norm1=(e1-mean(e1))/sqrt((sum(e1**2))/(n-2)) #标准化残差

plot(Z,e.norm1,ylab = "标准化残差") #绘制标准化残差关于响应变量sqrt(Y)的散点图