根据前序遍历和中序遍历构建二叉树

根据树前序遍历和中序遍历构建二叉树

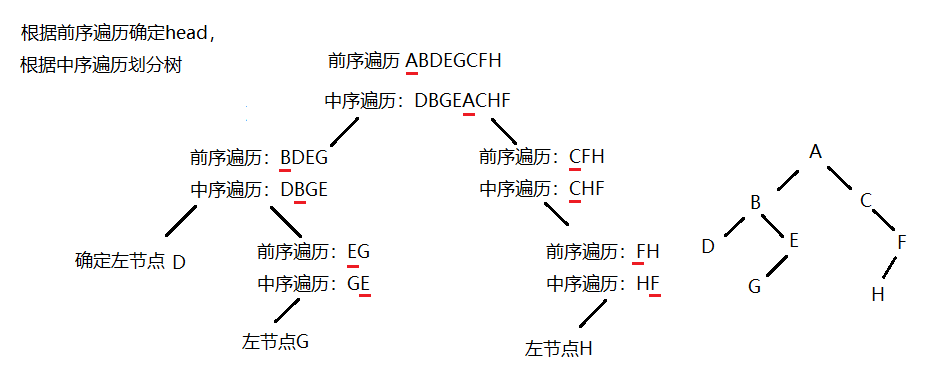
问题：已知一个二叉树前序遍历为：ABDEGCFH，中序遍历为：DBGEACHF，则该二叉树的后序遍历为？

思路是这样的：1：根据前序遍历来确定每次根节点的位置，因为前序遍历先访问的是根节点，所以前序遍历第一个位置就是根节点。 2：根据根节点和中序遍历将树划分为左右两棵树。3：根据第一步和第二步递归的处理左右两棵树。

第一步：根据前序遍历 A B D E G C F H 确定头结点是A，根据中序遍历 D B G E A C H F 将树划分为左子树 D B G E 和右子树 C H F。
第二步：划分为左右两棵子树：对于左子树，前序遍历是 B D E G，后续遍历是 D B G E。对于右子树，前序遍历是 C F H，后续遍历是 C H F。
第三步：对左子树和右子树分别运用第一步和第二步进行分析。
递归结束的条件：当中序遍历的节点只剩下一个节点的时候，那么这个节点就是叶子节点。

整体的操作流程如下：

Python代码如下：

class TreeNode:
    """树节点"""
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution:
    def reConstructBinaryTree(self, pre, tin):
        """根据前序遍历和中序遍历来重建一颗二叉树，要求前序遍历和中序遍历当中字符不重复
        Args:
          pre: 前序遍历  list类型或者者str类型
          tin: 中序遍历  
        Returns：
          head: 一个TreeNode类型的根节点
        """
        return self.rebuild_tree(pre, 0, len(pre)-1, tin, 0, len(tin)-1)

    def rebuild_tree(self, pre, pre_start, pre_end, tin, tin_start, tin_end):
         """递归的进行树的重建"""
        if pre_start > pre_end or tin_start > tin_end:
            return None

        head = TreeNode(pre[pre_start])
        tin_mid = tin.index(pre[pre_start])
        left_length = tin_mid - tin_start

        head.left = self.rebuild_tree(pre, pre_start+1, pre_start+left_length, 
                                      tin, tin_start, tin_mid-1)
        head.right = self.rebuild_tree(pre,pre_start+left_length+1, pre_end, 
                                       tin, tin_mid+1, tin_end)
                                       
        return head

def post_order_print(head):
    """以后序遍历的方式打印一颗二叉树"""
    if head is None:
        return
    post_order_print(head.left)
    post_order_print(head.right)
    print(head.val,end='')
if __name__ == '__main__':
    pre = 'ABDEGCFH'
    tin = 'DBGEACHF'
    s = Solution()
    head = s.reConstructBinaryTree(pre, tin)
    post_order_print(head)  # result: DGEBHFCA

根据树后序遍历和中序遍历构建二叉树

道理是一样的，根据后序遍历来确定根节点的位置，由于后序遍历最后访问根节点， 所以此时最后一个节点就是根节点。根据中序遍历来划分左右子树，然后迭代求解。

根据树前序遍历和后序遍历不能构建唯一的二叉树

前序和后序在本质上都是将父节点与子结点进行分离，但并没有指明左子树和右子树的能力，因此得到这两个序列只能明确父子关系，而不能确定一个二叉树。
比如前序遍历为ABC，后续遍历为CBA，可以构造出下面两棵树，可以发现这并不唯一：