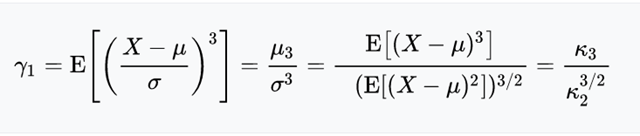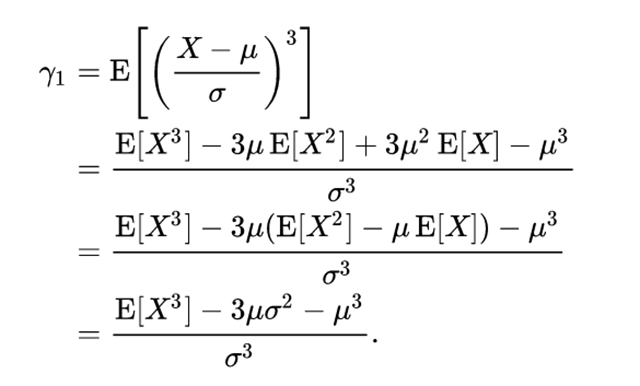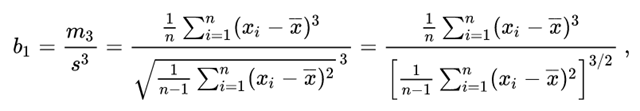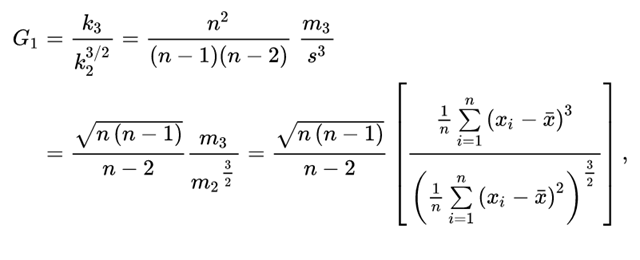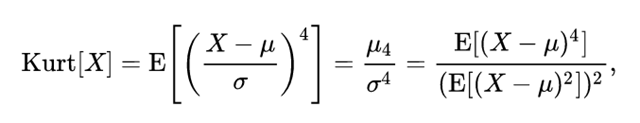偏度和峰度的计算
偏度(skewness)和峰度(kurtosis):
偏度能够反应分布的对称情况,右偏(也叫正偏),在图像上表现为数据右边脱了一个长长的尾巴,这时大多数值分布在左侧,有一小部分值分布在右侧。
峰度反应的是图像的尖锐程度:峰度越大,表现在图像上面是中心点越尖锐。在相同方差的情况下,中间一大部分的值方差都很小,为了达到和正太分布方差相同的目的,必须有一些值离中心点越远,所以这就是所说的“厚尾”,反应的是异常点增多这一现象。
偏度的定义:
样本X的偏度为样本的三阶标准矩
其中$\mu$是均值,$\delta$为标准差,E是均值操作。$\mu_3$是三阶中心距,$\kappa_t $是$t^{th}$累积量
偏度可以由三阶原点矩来进行表示:
样本偏度的计算方法:
一个容量为n的数据,一个典型的偏度计算方法如下:
其中$\bar x$为样本的均值(和$\mu$的区别是,$\mu$是整体的均值,$\bar x$为样本的均值)。s是样本的标准差,$m_3$是样本的3阶中心距。
另外一种定义如下:
$k_3$是三阶累积量$\kappa_3$的唯一对称无偏估计(unique symmetric unbiased estimator)($k_3$ 和 $\kappa_3$写法不一样)。$k_2=s^2$是二阶累积量的对称无偏估计。
大多数软件当中使用$G_1$来计算skew,如Excel,Minitab,SAS和SPSS。
峰度的定义:
峰度定义为四阶标准矩,可以看出来和上面偏度的定义非常的像,只不过前者是三阶的。
样本的峰度计算方法:
样本的峰度还可以这样计算:
其中$k_4$是四阶累积量的唯一对称无偏估计,$k_2$是二阶累积量的无偏估计(等同于样本方差),$m_4$是样本四阶平均距,$m_2$是样本二阶平均距。
同样,大多数程序都是采用$G_2$来计算峰度。
python使用pandas来计算偏度和峰度
import pandas as pd x = [53, 61, 49, 66, 78, 47] s = pd.Series(x) print(s.skew()) print(s.kurt())
它是用上面的$G_1$来计算偏度 $G_2$来计算峰度,结果如下:
0.7826325504212567 -0.2631655441038463
参考:
Skewness 维基百科给出了偏差的计算公式
Kurtosis 维基百科给出峰度的计算公式