线性模型和逻辑回归
基本概念
线性模型是用属性的线性组合来进行预测的函数:
对于一个n维的数据$\mathbf{x}=\{x_1,x_2,…,x_n\}$,要学的一组权重$w_1,w_2,…,w_n;b$,使得预测结果为:
$f(x) = w_1x_1 + w_2x_2+…+w_nx_n +d$
向量的形式是这样的$f(\mathbf{x}) = \mathbf{w}^T \mathbf{x}+b$
线性模型的权重可以代表每个属性所占有的比重,其中权值越大,代表这个属性越重要。所以线性的模型可以作为一种嵌入式的特征选择,使用它们的系数coefficient,sklearn中的模型属性coef_。与之对应的是树结构,使用importance_属性,这个属性是使用树分割时候的某种度量(比如信息熵或者基尼系数)来衡量属性的比重。
线性回归
我们先来看回归问题的线性模型,然后再来研究分类问题。因为线性在回归上面表现的比较简单而且容易理解。
一维数据集
并且先来看一下只有一个属性的数据,也就是我们最终要学得到 $f(x_i) = wx_i +b$。 使得预测的值$f(x_i)$与真实值$y_i$的差最小。
那么在这个过程当中我们使用哪种优化函数。对于回归问题,最经典的性能评估函数是均方误差$E(f;D)= \frac{1}{m} \sum_{i=1}^{m}{(\textbf{x}_i –y_i)}^2$,其中D是数据集。我们要使得均方误差最小。 从图形上解释就是:寻找一条直线,使得所有的点到直线的距离最短。
求解的方法:对函数求偏导数,等于0,就可以求出参数w和b的值。
多维数据集
好吧,我们现在来把问题扩展到高维数据集,其实问题的本质并没有变,只是求解的过程当中花费的力气大了一点。
对于多维,我们想要学到$f(\mathbf{x_i}) = \mathbf{w}^T \mathbf{x_i}+b$使得使得预测的值$f(\mathbf{x_i})$与真实值$y_i$的差最小。
这个时候我们将$\mathbf{w}$和b合并,形成一个新的参数$\hat{\mathbf{w}}$即$\hat{\mathbf{w}} = (\mathbf{w};b)$。并且我们用一个新的变量来表示原来数据集加上一列全部为1的数值。即X为
$$ \left[ \begin{matrix} x_{11} & x_{12} & \cdots & x_{1n} & 1\\ x_{21} & x_{22} & \cdots & x_{2n} & 1\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ x_{31} & x_{32} & \cdots & x_{3n} & 1 \\ \end{matrix} \right] $$
所以现在我们用这个式子来表示高维情况下的均方误差 $f(\hat{\mathbf{w}}) = {( \mathbf{y} – \mathbf{X} \hat{\mathbf{w}}) }^T ( \mathbf{y} – \mathbf{X} \hat{\mathbf{w}})$
维度说明:y为 $m \times 1$维,(m为数据集的个数,n为属性的个数) X为 $m \times (n+1)$维 $\hat{\mathbf{w}}$ 为 $(n+1) \times 1$维
好的,现在我们的目的就是使用某种优化方法来使得函数$f(\hat{\mathbf{w}}) $值最小。首先还是求导数。(由于缺乏一些矩阵求导的知识以及优化的知识,所以这一块比较困难)
$\frac{ \partial f(\hat{\mathbf{w}}) }{\partial \hat{\mathbf{w}}} $ = $ 2 \mathbf{X}^T (\mathbf{X} \hat{ \mathbf{w} }– \mathbf{y} ) $
当$\mathbf{X}^T \mathbf{X}$为满秩矩阵或者正定矩阵的时候,最优解为$(\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}$ 当矩阵不是满秩矩阵的时候需要引入正则化项,也就是把这个函数当做一个经验损失,需要添加一定的罚函数,变成结构损失。
广义线性模型
我们上面讨论的函数形式都是让线性模型的预测值逼近与y值,那么我们也可以让线性模型$ \mathbf{w}^T \mathbf{x}+b$逼近于y的变体,比如$ln(y)$。那么这个时候我们想让$ln(y) = \mathbf{w}^T \mathbf{x}+b$,更一般的我们可以考虑可微函数$g(\cdot) 使得 y = g^{-1}(\mathbf{w}^T \mathbf{x}+b)$。
广义线性模型实际上是将线性分类的结果映射到另外一个值域上面。对于基本的线性模型,实际上使用的是$y=f(x)$,它将线性空间映射到线性空间。对于$y=e^x$它将线性空间映射到对数空间。下面将会看到,使用sigmoid函数,是将线性空间映射到值域0到1之间,这样就能间接的来进行分类任务。
对数几率回归(逻辑回归 logistic regression)
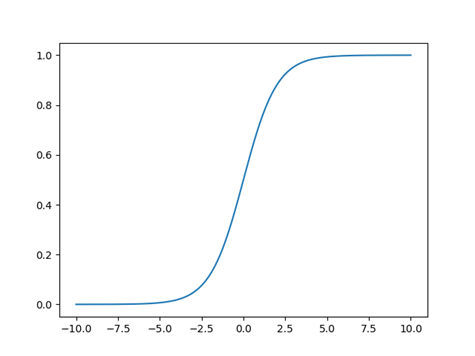
现在我们开始讨论对于分类问题我们应该如何去做。我们知道线性模型产生的结果是一个实数,而二分类问题输出的结果是{0,1}这样的标记。那么我们应该如何处理这个问题,最理想的情况下我们想要使用一个单位阶跃函数,使得线性结果预测>0的时候,输出为1,线性结果输出<0的时候,我们让输出为0,但是糟糕的是,阶跃函数并不是可微的。所以我们想要找一个可微的函数,sigmoid函数,它的图形像s形,这样的函数满足我们的要求。logistic 函数的形式如下
$y = \frac{1}{1+e^{-z}}$
函数图形如下:
这个函数其实并不是直接把线性的输出映射到标签上,而是映射到0到1之间的一个值,这是一个非常有意思的事情,我们可以用这个值来表示输出为正例的概率,比如当映射的值为0.8的时候,我们认为输出为正例的概率比较大,于是把它归为正类。当输出的值为0.2的时候,我们认为它输出为正类的概率比较小,于是判定为负类。 这种输出概率而不是直接输出类标签的方式在很多模型当中都很常见,事实上这也是一种非常有效的方法。 只有理解了这一点:使用逻辑函数以后输出的是一个概率值,那么后面的很多公式才可以理解。
使用逻辑函数以后的,模型的线性输出为 $z = \mathbf{w}^T \mathbf{x}+ b$,加上逻辑函数以后,把它转换为一个输出在0和1之间的y值,所以结果变为了:
$ y = \frac{1}{1 + e^{-(\mathbf{w}^T \mathbf{x}+ b)}}$,我们根据上面的论述,可以把y看做是输出为正例的概率。
这个函数可以变换为 $ln \frac{y}{1-y} = \mathbf{w}^T \mathbf{x}+ b$
y为输出为正例的概率,那么1-y是输出为负类的概率,所以两者的比值叫做“几率”,然后再取对数,顾这个函数叫做对数几率。
我们可以把这里的W和b看成一个参数$\theta$。
当y取1时,后验概率$p(y=1 | x; \theta) = h_{\theta}(x)$
当y取1时,后验概率$p(y=0 | x; \theta) = 1 - h_{\theta}(x)$
那么,可以将上面的式子写为一个式子:$p(y_i | x_i;\theta) = { h_{\theta} }^ {y_i} (1-h_{\theta})^{1-y_i}$
这里的$h_{\theta}(x) = \frac{1}{1+e^{-\theta x}}$
那么,我们如何求解$\theta$哪?我们利用参数估计当中的最大似然法来进行求解,它的基本思想是既然已经观察到了这些变量的取值,那么可以用使得这些取值发生的参数$\theta$作为整体$\theta$的估计。
似然函数求解
似然函数是一种参数估计的方法,在观察到一系列的值的情况下寻找最大的$\theat$值作为估计值。对数似然函数如下:
$$ln(L(\theta)) = \sum \limits_{i=1}^{m} lnp(y_i |x_i;\theta)$$
将$p(y_i | x_i;\theta) = { h_{\theta} }^ {y_i} (1-h_{\theta})^{1-y_i}$带入以后得到:
$$ln( L(\theta) )= \sum \limits_{i=1}^{m} ln ({h_{\theta} }^{y_i} ( (1-h_{\theta}))^{1-y_i})= \sum \limits_{i=1}^{m} (y_i ln(h_{\theta}) +(1-y_i) ln(1-h_{\theta}) ) $$
最大化似然函数等于最小化它的负值,所以最终的目标函数变为了
$$J(\theta) = –ln(L(\theta) = -\sum \limits_{i=1}^{m} (y_i ln(h_{\theta}) +(1-y_i) ln(1-h_{\theta}) ) $$
梯度下降求解
利用梯度下降法来求解的时候,则$\theta_j = \theta_j – \alpha \frac{\partial J(\theta)}{\partial \theta_j} $
$\frac{\partial J(\theta)}{\partial \theta_j} = –\sum \limits_{i=1}^{m} y_i \frac{1}{h_\theta} \frac{\partial h_\theta}{\partial \theta_j} + (1-y_i) \frac{-1}{1-h_\theta} \frac{\partial h_\theta}{ \partial \theta_j}$
其中$h_{\theta} = \frac{1}{1+e^{-\theta ^T x}}$
则$\frac{\partial h_\theta }{\partial \theta} = \frac{-1 \cdot e^{-\theta ^T x}( –x)}{(1+e^{-\theta ^T x})^2} = (1-h_{\theta}) h_{\theta}x$ 代入上式
$\begin{equation} \begin{split} \frac{\partial J(\theta)}{\partial \theta_j} &= –\sum \limits_{i=1}^{m} [y_i \frac{1}{h_\theta} \frac{\partial h_\theta}{\partial \theta_j} + (1-y_i) \frac{-1}{1-h_\theta} \frac{\partial h_\theta}{\theta_j}]\\ &=–\sum \limits_{i=1}^{m} [y_i \frac{1}{h_\theta} (1-h_{\theta}) h_{\theta}x_j + (1-y_i) \frac{-1}{1-h_\theta} (1-h_{\theta}) h_{\theta}x_j ]\\ &=\sum \limits_{i=1}^{m}(h_{\theta}(x_i)-y_i)x_j \end{split} \end{equation}$
另外一种表述方法
提供另外一种思路: 我们刚才$y \in \{0,1\}$,现在我们让$y \in \{-1,1\}$
这样我们可以运用一些策略了,因为我们总是想让 $y_i $和$\mathbf{w}^T \mathbf{x}+ b$ 的乘积大于0,所以把这两个的乘积看做一个变量,
我们令$p(Y=y|x) = \frac{1}{1+e^{ -y( \mathbf{w}^T \mathbf{x}+ b}) }$
我们希望对于每个变量,这个值越大越好。那么我们求似然函数,这个时候不用区分$p_0$和$p_1$,求解就变得简单很多:
对数似然函数:$ln(L(\mathbf{w},b) = \sum \limits_{i=1}^{m} ln (\frac{1}{ 1 + e^{-y_i ({\mathbf{w}}^T \mathbf{x}_i+ b)} })$
所以优化目标变为$J(\mathbf{w},b) = -ln(L(\mathbf{w},b) = \sum \limits_{i=1}^{m} ln( 1 + e^{-y_i ({\mathbf{w}}^T \mathbf{x}_i+ b)} )$ 。 sklearn 的Logistic Regression目标优化函数,就是这个函数再加一个正则项。
sklearn当中逻辑回归可以选用的参数
sklearn当中的优化函数我们上面说了,为:$\min \limits_{ w,c} C \sum \limits_{i=1}^{m} ln( 1 + e^{-y_i {\mathbf{w}}^T \mathbf{x}_i+ b} ) + 正则项$, 正则项又叫做罚函数。
所以sklearn中的参数有:
penalty: 罚函数项 L1或者L2,默认为l2. 选择不同的罚函数项目,后面的一些参数的选择也会受限。
C: 惩罚因子,默认为1,当C的值越大,表示对于错误的惩罚越大。
solver:求解的方法,也就是优化的时候使用的函数{‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’},newton-cg为牛顿法家族中的一种,lbfgs为拟牛顿法的一种,liblinear为开源liblinear实现,sag为随机平均梯度下降,saga为随机平均梯度下降的变体。
multi_class : 多分类时选择的策略, 可以选择{‘ovr’, ‘multinomial’},前者为one-vs-rest,后者为many-vs-many.
class_weight: 分配类型的权重。
线性判别分析(LDA)
线性判别分析也是使用一个线性函数$y = \mathbf{w}^T \mathbf{x} $,使用它的目的是把我们的数值映射到一维空间空间。当我思考一维空间是什么的时候,刚开始我以为是映射到一条直线上,的确书上就是这么画的,把我们的样本映射到一条直线上。 但是,假如考虑到高维,比如三维,难道是映射到一个平面上吗?不是的。理解这里的一维不应该从图形上面进行理解,而应该说y是一个数值,是一维的,所以把它映射到一维上面。
映射到一维上面以后,我们有一个直观的感受,我们想让同类样本之间的距离尽量靠近些,不同类样本之间的距离尽可能远一点。从这个思路出发,我们来定义我们的优化函数。 对于二分类问题{0,1},那么我们使用$\mu_0$和 $\mu_1$来表示第0类和第1类样本的均值,注意这里的$\mu_0$和 $\mu_1$为n维的向量,n为样本当中特征的个数。我们使用$\Sigma_0$和 $\Sigma_1$来表示第0类和第1类样本的协方差。
那么,为了使得两个样本的距离尽可能远,我们让它们的投影点之间的距离越大越好:即${ \Vert \mathbf{w}^T \mu_0 – \mathbf{w}^T \mu_1 \Vert }_2 ^2$越大越好。
为了让同类样本之间的距离尽可能近,我们让协方差投影尽可能大:即$\mathbf{w}^T \Sigma_0 \mathbf{w} + \mathbf{w}^T \Sigma_1 \mathbf{w}$ 越大越好。 这个公式是度量投影点之间的方差。
所以,我们的目标函数为:我们想让下面这个函数越大越好。
$J = \frac {{ \Vert \mathbf{w}^T \mu_0 – \mathbf{w}^T \mu_1 \Vert }_2 ^2} {\mathbf{w}^T \Sigma_0 \mathbf{w} + \mathbf{w}^T \Sigma_1 \mathbf{w}}$ = $\frac {{ \Vert \mathbf{w}^T (\mu_0 – \mu_1 ) \Vert }_2 ^2} {\mathbf{w}^T \Sigma_0 \mathbf{w} + \mathbf{w}^T \Sigma_1 \mathbf{w}}$ =$\frac { \mathbf{w}^T (\mu_0 – \mu_1) (\mu_0 – \mu_1)^T \mathbf{w}} {\mathbf{w}^T ( \Sigma_0 + \Sigma_1 ) \mathbf{w}} $
对这个函数变形,我们定义类内散度矩阵和类间散度矩阵。类内散度矩阵主要是公式的下半部分,$S_w = \Sigma_0 + \Sigma_1$,类间散度矩阵主要是公式的上半部分 $S_b = (\mu_0 – \mu_1) (\mu_0 – \mu_1)^T $,所以公式重写为
$J = \frac {\mathbf{w}^T S_b \mathbf{w}} {\mathbf{w}^T S_w \mathbf{w}}$ 所以,这个优化的目标叫做最大化类间距,最小化类内距。
求解的时候,使用拉格朗日乘子法,还有奇异值分解等进行求解。
参考:
周志华 机器学习



 浙公网安备 33010602011771号
浙公网安备 33010602011771号