拉普拉斯（Laplace）分布

Laplace分布的概率密度函数的形式是这样的：

$p(x) = \frac{1}{2 \lambda} e^{-\frac{\vert x –\mu \vert}{\lambda}}$   一般$\mu$的取值为0，所以形式如下：

$p(x) = \frac{1}{2 \lambda} e^{-\frac{\vert x \vert}{\lambda}}$

它是由两个指数函数组成的，所以又叫做双指数函数分布（double exponential distribution）

 

均值和方差

均值的求解,若X的概率密度函数为f(X),那么X的均值为 $E(X) = \int_{- \infty}^{+ \infty} xf(x) dx$，代入以后可以发现里面的积分函数为奇函数，所以均值为0.

方差根据$D(X) = E(X^2)-(E(X))^2$,因为后面一项为0,所以主要求前一项$E(X^2)$,$E(X^2) = \int_{- \infty}^{+ \infty} x^2f(x)dx$ 根据积分公式$\int udv = uv-vdu$进行求解，得到方差为$2{\lambda}^2$

 

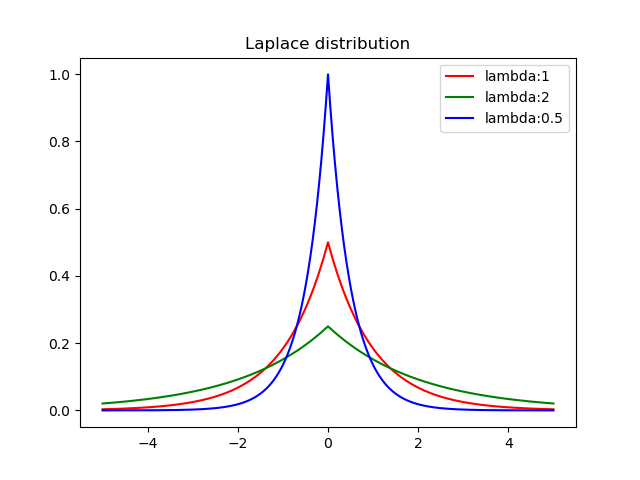
使用pyplot画概率分布图

import matplotlib.pyplot as plt
import numpy as np
def laplace_function(x, lambda_):
    return (1/(2*lambda_)) * np.e**(-1*(np.abs(x)/lambda_))
x = np.linspace(-5,5,10000)
y1 = [laplace_function(x_,1) for x_ in x]
y2 = [laplace_function(x_,2) for x_ in x]
y3 = [laplace_function(x_,0.5) for x_ in x]

plt.plot(x, y1, color='r', label="lambda:1")
plt.plot(x, y2, color='g', label="lambda:2")
plt.plot(x, y3, color='b', label="lambda:0.5")

plt.title("Laplace distribution")
plt.legend()
plt.show()

 

 

使用np.random.laplace获得随机样本的值

np.random.laplace可以获得拉普拉斯分布的随机值，参数主要如下：

loc：就是上面的$\mu$，控制偏移。

scale： 就是上面的$\lambda$控制缩放。

size：  是产生数据的个数

print(np.random.laplace(0,1,10))

产生结果如下：

[-0.56017859 -2.11417277 -1.05903743  1.7220117   0.68025748 -0.10421514
  -0.61471549  0.96146946 -3.40181804 -0.89675566]

 

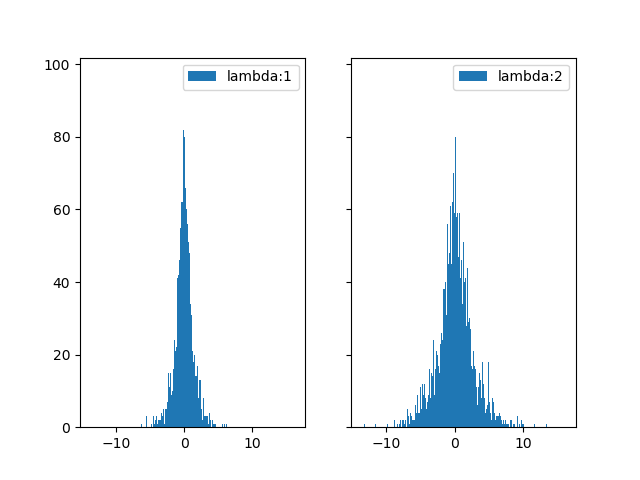
下面我们产生很多数据，然后用直方图把它们画出来，可以看出来它们符合Laplace分布。

import numpy as np
laplace1 = np.random.laplace(0, 1, 10000)
laplace2 = np.random.laplace(0, 2, 10000)

import matplotlib.pyplot as plt
fig, (ax1, ax2) = plt.subplots(1,2, sharex=True, sharey=True)
ax1.hist(laplace1,bins=1000, label="lambda:1")
ax1.legend()

ax2.hist(laplace2, bins=1000, label="lambda:2")
ax2.legend()
plt.show()