决策树算法
基本的决策树算法

上图是《机器学习》中的图
决策树算法是一个分治的递归算法,递归的终止条件有三种:
第一种:未选择划分属性之前,数据集D的类别属于同一类,这时将它划分为叶节点,类别划分为该类即可。
第二种:属性A为空,或者是数据集D在所有属性A上面取值相同,这时每条数据的值在A上,除了类别,都是一样的。将该叶节点划分为D中类别最多的类。
第三种:划分之后,划分后的数据集$D_v$为空,将该叶节点划分为D中最多的类。
下面我用一个例子来说明一下这三种情况。
Titanic简化数据集说明决策树在三种情况下返回
我们假设有下面的数据,这是从titanic数据里面简化出来的,属性有:
sex,乘客的性别,取值为female和male
pclass,等级,取值为1,2,3
embarked,登陆港口,取值为s,c
survived表示的是分类结果,1表示存活,0表示死亡
| sex | pclass | embarked | survived |
| f | 2 | s | 1 |
| f | 3 | c | 1 |
| m | 1 | s | 0 |
| m | 1 | s | 1 |
| m | 2 | s | 0 |
| m | 2 | c | 1 |
| m | 1 | s | 0 |
下面这幅图体现了上面三种情况,尖括号里面的值表示不同的情况。
sex为female的人全部存活下来,分类结果均为1,所以这属于第一种,以分类结果1作为叶子节点。
当sex为male的时候,pclass为1,我们可以发现,样本在属性上的取值相同,属于第二中情况,分类结果用样本中分类最多的类来表示。而pclass为2,embarked为s和c这两种情况均为A为空值这种情况,所以也属于第二类。
我们发现,我们的数据当中没有sex=male,pclass=3这种情况,我们直接用训练集当中分类最多的标签代替,这属于第三类。
常用的划分属性的策略
1:使用信息增益
运用信息熵的一些概念,在一个样本集合当中,样本的分类越“混乱”它的信息熵就越大,这个样本就越不纯,相反,一个样本越“整齐”,它的信息熵越小,这个样本就越纯。 样本的分类为[1,1,1,0]要比[1,1,0,0]好,前者比较“整齐”,较纯。所以,如果一个属性划分出来的样本越纯,那么我们就越倾向于选择这个属性。
D为样本集合,第k类样本所占的比例为$p_k(k=1,2,…,\vert y \vert)$,那么D的信息熵为
$Ent(D) = – \sum \limits_{i=i}^{k} p_k \log_2 p_k$
若以属性a来进行划分,属性a的可取值为${a^1,a^2,…,a^V}$,那么属性集D在$a^v$上的样本为$D^v$
那么,以属性a来对样本进行划分的信息增益为:
$Gain(D,a) = Ent(D) – \sum \limits_{v=1} ^{V} \frac {\vert D_v \vert}{\vert D \vert} Ent(D^v)$
信息增益率越大,表示使用属性a划分的结果越好。ID3算法以信息增益为准则进行属性选择
2:使用增益率
在使用信息增益率的时候观察到一个现象,一个属性的取值越多,它的信息增益越高,所以引入增益率来进行属性划分
$Gain\_ratio(D,a) = \frac {Gain(D,a)}{IV(a)}$ 其中 $IV(a) = – \sum \limits_{i=1} ^ {V} \frac {\vert D_v \vert}{\vert D \vert} \log_2 \frac {\vert D_v \vert}{\vert D \vert}$
C4.5算法就是以增益率为基础进行改进出来的
3:使用基尼指数
数据D的纯度可以用基尼值来进行衡量
$Gini(D) = \sum \limits_{k=1} ^{\vert y \vert} \sum \limits_{k’ \neq k} p_k p_{k’} $ = $1 - \sum \limits_{k=1} ^{\vert y \vert} p_k ^2$
在基尼值上面定义的基尼指数为:
$Gini\_index(D,a) = \sum \limits_{v=1} ^{V} \frac {\vert D_v \vert}{\vert D \vert} Gini(D^v)$
选择基尼指数最小的属性值a进行划分,CART(classification and Regression Tree)是以基尼指数来选择属性的。
CART分类树是一个二分类树,在选取划分点的时候,是寻找所有属性的所有划分点的里面寻找最小基尼指数,以该划分点作为树分割的条件,左子树是所有数据集的取值等于该划分点的值,右子树是不等于该划分点的值,而不是取该属性下的n个所有的点构成一颗n叉树。
剪枝处理
剪枝是为了获得更好的泛化性能,剪枝分为预剪枝与后剪枝。
预剪枝是在决策树建立的时候,将某些可以分割的节点当做一个叶子节点,来和分割以后的节点进行比较。 叶子节点的分类值可以采用决策树算法的第二种情况:将叶子节点的类别设为数据集当中样本最多的类别。 然后用某种方法进行评估。
后剪枝是在决策树已经建立的基础上,把某些分割的点用叶子节点来替代,观察性能。
连续值和多变量
处理连续值的时候,要在连续属性当中选择一个合适的分割点来进行属性的划分,分割点的选择是在诸多数值里面选择一个能够使得信息增益最大的一个,而不仅仅是选择连续属性当中中间的值。
而多变量意味着划分属性的时候不单单选择一个属性来进行划分,可以选择多个属性进行划分。
sklearn当中的决策树
这个博客里面讲的很清楚:scikit-learn决策树算法类库使用小结,讲了各种参数
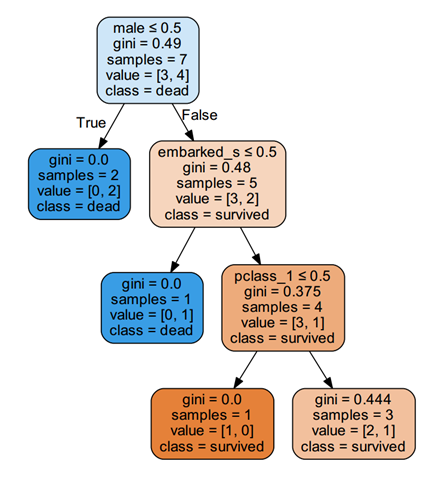
尝试使用博客里面的算法对上述数据进行处理,并使用graphviz画图:
from sklearn.tree import DecisionTreeClassifier from sklearn import tree import pandas as pd path = r"C:\Users\xiaotiange\Desktop\tic.csv" dt = DecisionTreeClassifier() titanic = pd.read_csv(path) from sklearn.preprocessing import LabelEncoder le = LabelEncoder() z1 = pd.get_dummies(titanic['sex']) z2 = pd.get_dummies(titanic['pclass']) z3 = pd.get_dummies(titanic['embarked']) X = pd.concat([z1,z2,z3], axis=1) X.columns = ['female', 'male','pclass_1', 'pclass_2', 'pclass_3', 'embarked_c','embarked_s'] y = titanic['survived'] dt.fit(X,y) f_names= X.columns t_names = ['survived', 'dead'] dot_data = tree.export_graphviz(dt, out_file=None, feature_names=f_names, class_names=t_names, filled=True, rounded=True, special_characters=True) import pydotplus graph = pydotplus.graph_from_dot_data(dot_data) graph.write_pdf("titanic.pdf")




 浙公网安备 33010602011771号
浙公网安备 33010602011771号