双向链表与LRU算法实现


undefinedundefined

双向链表与LRU算法

各位好久不见啊，由于疫情原因笔者一直宅在家中做考研复习。俗语云：积少成多，跬步千里。于是我在此做一个简单分享，一步步记录我的学习历程。

先从单链表谈起#

道家有言：一生二,二生三,三生万物 ，万物皆有源头，在说双向链表之前让我们先看看单链表吧。

我们在学习计算机编程语言时，最先接触的数据结构是线性表，线性表是逻辑结构，其根据存储方式的不同，又分为 顺序表，链表。而 单链表是链表中最基础的结构。

如下图所示，

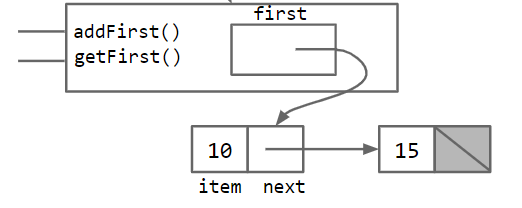
其中，我们有两个节点，第一个节点的值为10，并拥有一个指针指向下一个节点15。

可能的类代码：

Copy
public class SLList {
   private IntNode first;
   public SLList() {
      first = null;
   }

   public SLList(int x) {
      first = new IntNode(x, null);
   }
 
   public void addFirst(int x) {
      first = new IntNode(x, first);
   }
   public int getFirst() {
  	  return first.item;
   }
}

规范——哨兵节点的诞生#

在上面的单链表中，我们实现了从头结点插入的功能，如果我们要实现从链表的尾部插入的功能呢？

我们可能会这样写：

Copy
public void addLast(int x) {
      size += 1;
      IntNode p = first;
      while (p.next != null) {
         p = p.next;
      }
      p.next = new IntNode(x, null);
   }

但是，如果我们要插入到一个空链表时，因为 first本身是 null ，当我们运行到 while(p.next != null)时，程序会发生错误！

有的同学就会想到，那我们加一个 if 处理不就行了。

Copy
if (first == null) {
    first = new IntNode(x, null);
    return;
  }
while(p.next != null){
    p = p.next;
}
p.next = new IntNode(x,null);

但是，这样处理问题会显得不美观。而且当你处理的特殊情况越来越多的时候，你的代码会越来越长，导致难以阅读和维护，并破坏了简单设计的原则。

这个时候我们的大救星，哨兵节点，闪亮登场。

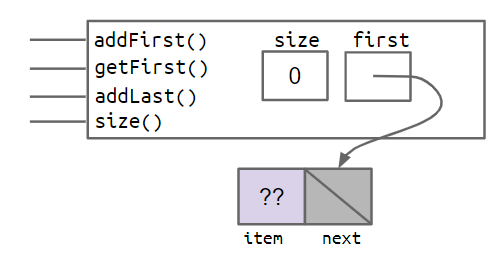
如上图所示，我们在初始化空链表时，会创建一个哨兵节点，他不存储值，只是提供了一个守门员的角色，帮助你看看门外有没有人并帮助你寻找后面的节点。我们把它叫做 sentinel。

这样我们就不用担心会遇到空节点的情况，万岁。事情变得简单和规范化了，没有特殊例子！

我们可以这样写代码了,去掉了 if语句：

Copy
IntNode p = sentinel;
  while (p.next != null) {
    p = p.next;
  }
p.next = new IntNode(x,null);

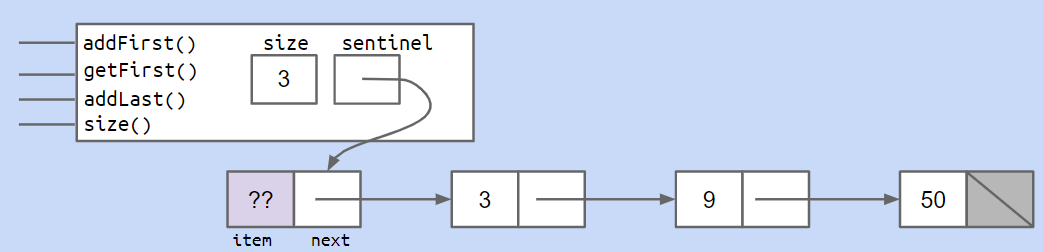
够不着怎么办#

我们解决了从头部插入和从尾部插入的问题，但是如果我们要删除最后一个节点呢？时间复杂度是多少？

显然，我们要从头节点，一直找下去，直到导数第二个节点，时间复杂度为 O(n)。有没有办法缩短时间呢？

终极进化#

如果我们想要删除最末尾的节点，显然我们要找到最后的节点和倒数第二个节点，所以我们可以添加一个指向上一个节点的指针。并添加指向最末尾的指针，一直指向最后一个节点。

这样的结构够好么？别忘了还有我们的哨兵朋友们！

最后综合上述原因，我们造出了带有哨兵节点的双向链表！如下图所示：

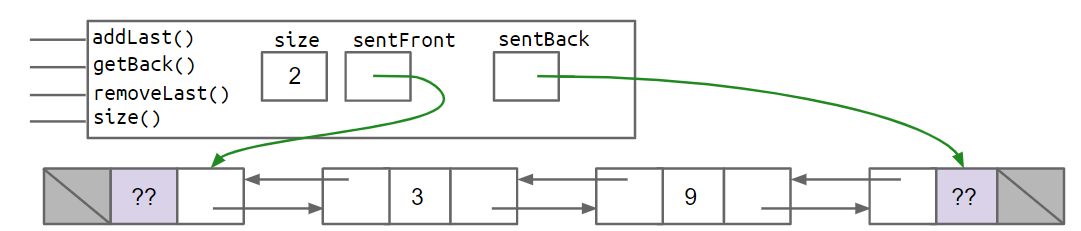
双向链表的实现#

上面我们讲了双向链表的由来，这里我们正式实现双向链表：

API：

  • addFirst : 头插入
  • removeFirst: 删除头节点
  • addLast: 尾插入
  • removeLast: 删除尾节点
Copy
public class DLList<T> {
    // 使用了泛型实现双向链表
    private TNode sentinel;
    private int size;

    // 新建内部类,节点
    public class TNode{
        TNode prev;
        TNode next;
        T item;
        public TNode(T item,TNode prev,TNode next){
            this.item = item;
            this.prev = prev;
            this.next = next;
        }
    }
	// 新建空链表
    public DLList(){
        sentinel = new TNode(null,null,null);
        sentinel.prev = sentinel.next = sentinel;
        size = 0;
    }

    public void addFirst(T item){
        TNode newNode = new TNode(item,sentinel,sentinel.next);
        sentinel.next.prev = newNode;
        sentinel.next = newNode;
        size+=1;

    }
    public boolean validateIndex(int index){
        if(index<0||index>=size){
            return false;
        }
        return true;
    }
    /*
     * helper method to get the node we need
     * */
    private TNode getNode(int index){
        TNode res;
        if(index<size/2){
            res = sentinel.next;
            for (int i=0;i<index;i++){
                res = res.next;
            }
            return res;
        }
        res = sentinel.prev;
        int newIndex = size - index -1;
        for (int i = 0 ;i<newIndex;i++){
            res = res.prev;
        }
        return res;
    }

    public T get(int index){
        if(!validateIndex(index)) return null;
        return getNode(index).item;
    }


    public int size(){
        return size;
    }
    public boolean isEmpty(){
        return size==0;
    }
    public void addLast(T item){
        TNode newNode = new TNode(item,sentinel.prev,sentinel);
        sentinel.prev.next = newNode;
        sentinel.prev = newNode;
        size+=1;
    }
    /*
     * helper method to delete the node we want
     * */
    private T delete(int index){
        if(!validateIndex(index)) throw new IndexOutOfBoundsException();
        TNode cur = getNode(index);
        T res = cur.item;
        cur.prev.next = cur.next;
        cur.next.prev = cur.prev;
        cur = null;
        size--;
        return res;
    }
    public T removeLast(){
        return delete(size-1);
    }

    public T removeFirst(){
        return  delete(0);
    }
}

LRU算法#

学习过计算机操作系统的小伙伴，一定知道我们管理内存时需要页面置换算法。其中一种经典的算法就是LRU算法（最近最久未使用算法）。

利用双向链表，我们可以软件模拟这种操作。每次使用数据，或者插入新数据的时候，我们把它移动到头部。

这样越靠近头部的就是我们经常使用的数据。而当数据满了的时候，我们只要删除尾部的节点就好了，因为他是最久未使用的数据。

众所周知，链表的遍历是线性的，当我们要查询数据的时候，速度并不理想。于是我们引入哈希表加速查找。

具体实现#

LRU 缓存机制可以通过哈希表辅以双向链表实现，我们用一个哈希表和一个双向链表维护所有在缓存中的键值对。

双向链表按照被使用的顺序存储了这些键值对，靠近头部的键值对是最近使用的，而靠近尾部的键值对是最久未使用的。

哈希表即为普通的哈希映射（HashMap），通过缓存数据的键映射到其在双向链表中的位置。

这样一来，我们首先使用哈希表进行定位，找出缓存项在双向链表中的位置，随后将其移动到双向链表的头部，即可在 O(1), O(1) 的时间内完成 get 或者 put 操作。具体的方法如下：

对于 get 操作，首先判断 key 是否存在：

如果 key 不存在，则返回 -1−1；

如果 key 存在，则 key 对应的节点是最近被使用的节点。通过哈希表定位到该节点在双向链表中的位置，并将其移动到双向链表的头部，最后返回该节点的值。

对于 put 操作，首先判断 key 是否存在：

如果 key 不存在，使用 key 和 value 创建一个新的节点，在双向链表的头部添加该节点，并将 key 和该节点添加进哈希表中。然后判断双向链表的节点数是否超出容量，如果超出容量，则删除双向链表的尾部节点，并删除哈希表中对应的项；

如果 key 存在，则与 get 操作类似，先通过哈希表定位，再将对应的节点的值更新为 value，并将该节点移到双向链表的头部。

上述各项操作中，访问哈希表的时间复杂度为 O(1)O(1)，在双向链表的头部添加节点、在双向链表的尾部删除节点的复杂度也为 O(1)O(1)。而将一个节点移到双向链表的头部，可以分成「删除该节点」和「在双向链表的头部添加节点」两步操作，都可以在 O(1)O(1) 时间内完成。

代码如下：

Copy
public class LRUCache {
    class DLinkedNode {
        int key;
        int value;
        DLinkedNode prev;
        DLinkedNode next;
        public DLinkedNode() {}
        public DLinkedNode(int _key, int _value) {key = _key; value = _value;}
    }

    private Map<Integer, DLinkedNode> cache = new HashMap<Integer, DLinkedNode>();
    private int size;
    private int capacity;
    private DLinkedNode head, tail;

    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        // 使用伪头部和伪尾部节点
        head = new DLinkedNode();
        tail = new DLinkedNode();
        head.next = tail;
        tail.prev = head;
    }

    public int get(int key) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            return -1;
        }
        // 如果 key 存在，先通过哈希表定位，再移到头部
        moveToHead(node);
        return node.value;
    }

    public void put(int key, int value) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            // 如果 key 不存在，创建一个新的节点
            DLinkedNode newNode = new DLinkedNode(key, value);
            // 添加进哈希表
            cache.put(key, newNode);
            // 添加至双向链表的头部
            addToHead(newNode);
            ++size;
            if (size > capacity) {
                // 如果超出容量，删除双向链表的尾部节点
                DLinkedNode tail = removeTail();
                // 删除哈希表中对应的项
                cache.remove(tail.key);
                --size;
            }
        }
        else {
            // 如果 key 存在，先通过哈希表定位，再修改 value，并移到头部
            node.value = value;
            moveToHead(node);
        }
    }

    private void addToHead(DLinkedNode node) {
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }

    private void removeNode(DLinkedNode node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    private void moveToHead(DLinkedNode node) {
        removeNode(node);
        addToHead(node);
    }

    private DLinkedNode removeTail() {
        DLinkedNode res = tail.prev;
        removeNode(res);
        return res;
    }
}

更多#

引用：

^1链表定义

^2缓存文件置换机制

^3leetcode

posted @   Mikejiawei  阅读(1300)  评论(1)  编辑  收藏  举报
编辑推荐：
· Linux系列：如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列：如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列（二）：开始使用ML.NET
阅读排行：
· 被坑几百块钱后，我竟然真的恢复了删除的微信聊天记录！
· 没有Manus邀请码？试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单，K8s 太复杂？w7panel 让容器管理更轻松！
CONTENTS
✕
点击右上角即可分享
微信分享提示