2016/5/21 星期六 21:38
| desc | |
| 关于矩阵分解 |
LSA pLSA LDA 本质都是矩阵分解
1. LSA 的奇异值分解 A = S·Σ·D,分解得到的是三个矩阵,操作一下,就是
S' = S·Σ
D' = Σ·D
此时 S' · D' 仍旧能够得到 近似原始矩阵的值
# 或者这里的 Σ 全部取 Σ' 即 :Σ' = sqrt( Σ )
这样的话,乘完毕以后还能得到原始的矩阵 A
这个 trick 将 分解为三个矩阵 转换为 分解为两个矩阵
2. pLSA 通过引入 topic A = B·C 两个矩阵
3. MF 矩阵分解的方法,与 pLSA 的问题相同,但是不是用 EM算法,而是数值解法,去逼近
直接得到 A = P·Q
4. 而你想要的 是 GloVec 的方法,即 input 矩阵是 一个方阵,是对称方阵
然后 希望 get 一个 矩阵(list of vector)
这些 vector 两两相乘 可以逼近 原始对称方阵
其实 这部分的代码 与 MF 的代码相似
summary 矩阵分解的方法【观点】
· EM 算法 的方法
· 数值逼近的方法 cost
· LDA 吉布斯采样
· SVD 分解
|
| 矩阵分解的 tool |
libSVD
libMF
libFM
svd feature
都可以做矩阵分解
|
| 冷启动的概念: |
1. 冷启动就是没有用户的历史行为数据,如何给用户做推荐遇到问题
新加入用户或商品因为没有历史数据所以很难做推荐
2. 只要是推荐系统都会遇到 这个问题,no matter CF or content based
|
|
推荐的本质与假设
不要本末倒置
|
推荐的根本是:满足用户的需求,是挖掘用户的需求再推,这是核心
现在的几个假设:(不一定真)
· 相似,买过A,可能还会买与A相似的A',基于此,才会找相似
· 搭配 是用户需求的补充
淘宝现在是,看过的就会推
其实这就是:相似法 和 搭配法 方法的PK
经过内部实验,发现:虽然搭配推荐看似好,但是对于转化率来说,不如 传统的相似推荐
所以现在的淘宝还是 以基于相似的方法为主
|
| 搭配推荐的思路 |
1. 基于模型的推荐:learning2rank
使用待搭配item 的特征向量的融合(拼接,相加,笛卡尔积),然后输入 排序模型,得到分值
2. 可以用是关联规则,基于规则
|
| 阿里面试的问题,现在才有观点啊 |
· 推荐中相似度的计算方法
· 协同过滤推荐的基本思路
· 机器学习的一般流程
而这三个 你都没有 回答上来 【观点】
|
| 看待RNN 的角度 |
· 二叉树形状的 网络结构
· 各个不同的门,其实就是:多个 feature map【观点】
|
| 推荐系统与产品 |
1. 增加推荐理由,会很大提高 卖出率
eg:
你的 5 个朋友有4个买了这个书
我知道你最近买了A,建议你买B,这个是A 的补
2. 一个app 着重做这两个点,推荐系统中的 新颖度(他们不知道的) 和 惊喜度(不相似但满意) 这两个 指标
如果这两个做得好,那么这个 app 会很快火起来
|
| 工业上的推荐系统 |
都是 多个 方法的 merge
word2vec
MF
CF
learning2rank
而不是单一的 一个模型的 综合
因为在乎稳定性
|
| 推荐中的评价指标 |
RMSE 中文是均方根误差
root mean square error
|
| 利用word2vec |
1. 使用 用户的 行为序列,即 次次点击的 商品item 序列
然后 对item 进行 word2vec 尝试,然后将 每个商品 vector 化
从而 基于第一类假设,可以有 相似的商品 来进行跑排序,以进行推荐
2. word2vec 本身已经体现了 序列的学习,即 next word
优点:
解决的问题是 , CF找回不够,因为:
使用协同过滤的时候 每个商品id,其实就是 太离散了,所以用 低维度向量表示每个商品,那么 相当于降维
|
| 推荐系统选取的各个feature 的评价 |  |
| 与搜索引擎的关系 |
对搜索引擎的 两个角度的改善
1. QA,不返回页面,而是具体答案
2. 推荐系统,直接给出猜你想看的
所以 QA,推荐系统,CTR ,都依赖于 搜索引擎的原理
|
| 提高覆盖率 |
就是 防止马太效应
即 越热越推,越推越热
|
| 提高多样性 |
就是:给用户更多的选择
推荐100件衬衫也是只能买一件
|
| 对于打分的预处理需要注意: |
每行去均值,再去相似度比较
去均值其实就是 因为有人 偏向高分低分,是为了消除用户的【评分尺度】
|
| item CF > user CF |
工业界:一般用于 item Collaborative filtering
因为:
1. 用户量> 商品量:比如 电影一共就几万部
2. 稳定度高:即两本书的相似度持久
两本书的相似度 今年 和 去年一半一样
而 user 的相似度会变化
|
| 商品关联 |
两个角度
1. 在电商领域有很多 同款但不完全一样的商品,会当成两个item
所以需要提前 做好关联
其实就是降低稀疏性,合并相似的
2. 如果 A、B 用户不能计算相似度,但是 AC 可以,BC 可以,那么就可以间接得到 AB 的相似度
|
| 关于冷启动问题 的解决 |
1.对于 新用户
用户注册的时候就要提供信息,或者使用互动的方式进行 用户信息的获取
社交数据 或者 标签数据
2. 对于新商品
根据商品的属性,可以基于规则 给出与 其它商品的 相似度,然后再基于 item based CF 推荐
|
| 推荐系统的观点 |
input 一个 不满的矩阵
output 缺失的值
因为是矩阵,所以 才有很多与矩阵相关的操作
|
| 基于矩阵分解必须要正则化 |
因为要防止过拟合,否则 拟合出来 还是 0
 |
| 打分系统如果增加偏置的化,可能效果会好 |
关于矩阵分解,因为有打分体系,所以特别指出:要加上偏置
对于 每一个 拟合的值
多加了 μ整体平均,和 user 与 item 的各自偏置
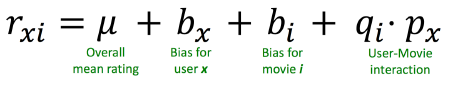 |
| wordvec经验 | 一般上 300~ 500 维度才是好的 |
| 矩阵拟合的代码 |
#简单的张量分解进行打分和推荐
#要用到numpy模块
import numpy
#手写矩阵分解
#现在有很多很方便对高维矩阵做分解的package,比如libmf, svdfeature等
def matrix_factorization(R, P, Q, K, steps=5000, alpha=0.0002, beta=0.02):
Q = Q.T
for step in xrange(steps):
for i in xrange(len(R)):
for j in xrange(len(R[i])):
if R[i][j] > 0:
eij = R[i][j] - numpy.dot(P[i,:],Q[:,j])
for k in xrange(K):
P[i][k] = P[i][k] + alpha * (2 * eij * Q[k][j] - beta * P[i][k])
Q[k][j] = Q[k][j] + alpha * (2 * eij * P[i][k] - beta * Q[k][j])
eR = numpy.dot(P,Q)
e = 0
for i in xrange(len(R)):
for j in xrange(len(R[i])):
if R[i][j] > 0:
e = e + pow(R[i][j] - numpy.dot(P[i,:],Q[:,j]), 2)
for k in xrange(K):
e = e + (beta/2) * (pow(P[i][k],2) + pow(Q[k][j],2))
if e < 0.001:
break
return P, Q.T
|




