密度聚类算法的DBSCAN
DBSCAN
problem
- 用你自己熟悉的语言,编写程序,用你所学的任何一种聚类算法,对所给定的数据集进行聚类挖掘,给出具体程序和挖掘结果。
密度聚类算法
- 密度聚类方法的指导思想1是,只要一个区域中的点的密度大于某个域值,就把它加到与之相近的聚类中去。这类算法能克服基于距离的算法只能发现“类圆形”的聚类的缺点,可发现任意形状的聚类,且对噪声数据不敏感。但计算密度单元的计算复杂度大,需要建立空间索引来降低计算量,且对数据维数的伸缩性较差。这类方法需要扫描整个数据库,每个数据对象都可能引起一次查询,因此当数据量大时会造成频繁的I/O操作。代表算法有:
DBSCAN、OPTICS、DENCLUE算法等。 DBSCAN(Density-Based Spatial Clustering of Applications with Noise)一个比较有代表性的基于密度的聚类算法。与划分和层次聚类方法不同,它将簇定义为密度相连的点的最大集合,能够把具有足够高密度的区域划分为簇,并可在有“噪声”的空间数据库中发现任意形状的聚类。
DBSCAN
-
定义 5-3 对象的
ε-邻域:给定对象在半径ε内的区域。 -
定义 5-4 核心对象:如果一个对象的
ε-临域至少包含最小数目MinPts个对象,则称该对象为核心对象。 -
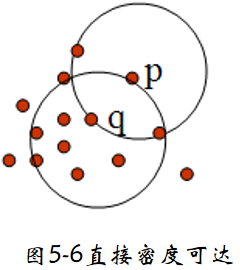
例如,在图5-6中,\(ε=1cm\),\(MinPts=5\),q是一个核心对象。
-
定义 5-5 直接密度可达:给定一个对象集合D,如果p是在q的
ε-邻域内,而q是一个核心对象,我们说对象p从对象q出发是直接密度可达的。 -
例如,在图5-6中,\(ε=1cm\),\(MinPts=5\),q是一个核心对象,对象p从对象q出发是直接密度可达的。
-
定义 5-6 密度可达的:如果存在一个对象链\(p_1,p_2,\cdots,p_n,p_1=q,p_n=p,p_i∈D,(1\le i \le n)\),\(p_{i+1}\)是从\(p_i\)关于ε和
MitPts直接密度可达的,则对象p是从对象q关于ε和MinPts密度可达的。 -
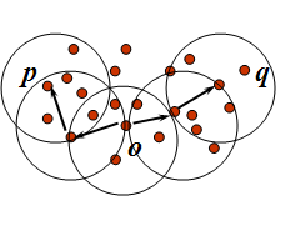
例如,在图5-7中,\(ε=1cm\),\(MinPts=5\),q是一个核心对象,\(p_1\)是从q关于ε和
MitPts直接密度可达,p是从\(p_1\)关于ε和MitPts直接密度可达,则对象p从对象q关于ε和MinPts密度可达的。 -
定义 5-7密度相连的:如果对象集合D中存在一个对象o,使得对象p和q是从o关于ε和
MinPts密度可达的,那么对象p和q是关于ε和MinPts密度相连的。 -
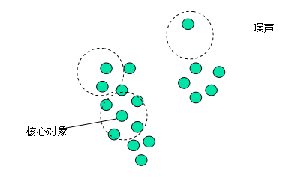
定义 5-8噪声: 一个基于密度的簇是基于密度可达性的最大的密度相连对象的集合。不包含在任何簇中的对象被认为是“噪声”。

算法描述
DBSCAN通过检查数据集中每个对象的ε-邻域来寻找聚类。如果一个点p的ε-邻域包含多于MinPts个对象,则创建一个p作为核心对象的新簇。然后,DBSCAN反复地寻找从这些核心对象直接密度可达的对象,这个过程可能涉及一些密度可达簇的合并。当没有新的点可以被添加到任何簇时,该过程结束。具体如下:
DBSCAN算法描述
算法5-5 DBSCAN
输入:包含n个对象的数据库,半径ε,最少数目MinPts。
输出:所有生成的簇,达到密度要求。
1. REPEAT
2. 从数据库中抽取一个未处理过的点;
3. IF 抽出的点是核心点 THEN找出所有从该点密度可达的对象,形成一个簇
4. ELSE 抽出的点是边缘点(非核心对象),跳出本次循环,寻找下一点;
5. UNTIL 所有点都被处理;
算法举例
下面给出一个样本事务数据库(见左表),对它实施DBSCAN算法。
根据所给的数据通过对其进行DBSCAN算法,以下为算法的步骤(设\(n=12\),用户输入\(ε=1\),\(MinPts=4\))
- 样本事务数据库
| 序号 | 属性 1 | 属性 2 |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 4 | 0 |
| 3 | 0 | 1 |
| 4 | 1 | 1 |
| 5 | 2 | 1 |
| 6 | 3 | 1 |
| 7 | 4 | 1 |
| 8 | 5 | 1 |
| 9 | 0 | 2 |
| 10 | 1 | 2 |
| 11 | 4 | 2 |
| 12 | 1 | 3 |
DBSCAN算法执行过程示意
| 步骤 | 选择的点 | 在ε中点的个数 | 通过计算可达点而找到的新簇 |
|---|---|---|---|
| 1 | 1 | 2 | 无 |
| 2 | 2 | 2 | 无 |
| 3 | 3 | 3 | 无 |
| 4 | 4 | 5 | 簇\(C_1:\{1,3,4,5,9,10,12\}\) |
| 5 | 5 | 3 | 已在一个簇\(C_1\)中 |
| 6 | 6 | 3 | 无 |
| 7 | 7 | 5 | 簇\(C_2:\{2,6,7,8,11\}\) |
| 8 | 8 | 2 | 已在一个簇\(C_2\)中 |
| 9 | 9 | 3 | 已在一个簇\(C_1\)中 |
| 10 | 10 | 4 | 已在一个簇\(C_1\)中 |
| 11 | 11 | 2 | 已在一个簇\(C_2\)中 |
| 12 | 12 | 2 | 已在一个簇\(C_1\)中 |
聚出的类为{1,3,4,5,9,11,12},{2,6,7,8,10}。
第1步,在数据库中选择一点1,由于在以它为圆心的,以1为半径的圆内包含2个点(小于4),因此它不是核心点,选择下一个点。
第2步,在数据库中选择一点2,由于在以它为圆心的,以1为半径的圆内包含2个点,因此它不是核心点,选择下一个点。
第3步,在数据库中选择一点3,由于在以它为圆心的,以1为半径的圆内包含3个点,因此它不是核心点,选择下一个点。
第4步,在数据库中选择一点4,由于在以它为圆心的,以1为半径的圆内包含5个点,因此它是核心点,寻找从它出发可达的点(直接可达4个,间接可达3个),聚出的新类{1,3,4,5,9,10,12},选择下一个点。
第5步,在数据库中选择一点5,已经在簇1中,选择下一个点。
第6步,在数据库中选择一点6,由于在以它为圆心的,以1为半径的圆内包含3个点,因此它不是核心点,选择下一个点。
第7步,在数据库中选择一点7,由于在以它为圆心的,以1为半径的圆内包含5个点,因此它是核心点,寻找从它出发可达的点,聚出的新类{2,6,7,8,11},选择下一个点。
第8步,在数据库中选择一点8,已经在簇2中,选择下一个点。
第9步,在数据库中选择一点9,已经在簇1中,选择下一个点。
第10步,在数据库中选择一点10,已经在簇1中,选择下一个点。
第11步,在数据库中选择一点11,已经在簇2中,选择下一个点。
第12步,选择12点,已经在簇1中,由于这已经是最后一点所有点都以处理,程序终止。
算法的性能分析
DBSCAN需要对数据集中的每个对象进行考察,通过检查每个点的ε-领域来寻找聚类,如果某个点p为核心对象,则创建一个以该点p为核心对象的新簇,然后寻找从核心对象直接密度可达的对象。如下表所示,如果采用空间索引,DBSCAN计算复杂度是\(O(n \log {n})\),这里n是数据库对象的数目。否则,计算复杂度是\(O(n^2)\)。
| 时间复杂度 | 一次邻居点的查询 | DBSCAN |
|---|---|---|
| 无索引 | \(O(n)\) | \(O(n^2)\) |
| 有索引 | \(\log n\) | \(n\log n)\) |
DBSCAN算法将是具有足够高密度的区域划分为簇,并可以在带有“噪声”的空间数据库中发现任意形状的聚类。但是,该算法对用户定义的参数是敏感的,ε、MinPts的设置将影响聚类的效果。设置的细微不同,会导致聚类结果的很大差别。为了解决上述问题,OPTICS(Ordering Points To Identify the Clustering Structure)被提出,它通过引入核心距离和可达距离,使得聚类算法对输入的参数不敏感。


