决策树分类
ID3 算法是建立在奥卡姆剃刀（用较少的东西，同样可以做好事情）的基础上：越是小型的决策树越优于大的决策树。C4.5 算法最大的特点是克服了 ID3 对特征数目的偏重这一缺点，引入信息增益率来作为分类标准。ID3 和 C4.5 虽然在对训练样本集的学习中可以尽可能多地挖掘信息，但是其生成的决策树分支、规模都比较大，CART 算法的二分法可以简化决策树的规模，提高生成决策树的效率。CART（Classification and Regression Tree，分类回归树），从名字就可以看出其不仅可以用于分类，也可以应用于回归。其回归树的建立算法上与分类树部分相似。
problem
- 用你自己熟悉的语言，编写程序（ID3算法，C4.5算法中的一种）对所给定的数据集进行分类挖掘，给出具体程序和挖掘结果，结果要求包含决策树的树形图以及分类规则。
- 利用自己的分类规则对未分类数据集进行分类，给出分类结果。
- 报告格式以信计专业的实验报告格式为准。
- 训练数据
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | class |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 27 | 0 | 1 | 0 | 2 |
| 0 | 1 | 0 | 27 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 27 | 1 | 0 | 0 | 2 |
| 0 | 0 | 1 | 24 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 30 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 31 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 37 | 1 | 0 | 0 | 2 |
| 0 | 0 | 1 | 22 | 0 | 0 | 1 | 2 |
| 0 | 0 | 1 | 25 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 34 | 1 | 1 | 0 | 2 |
| 0 | 1 | 0 | 33 | 1 | 1 | 0 | 2 |
| 0 | 0 | 1 | 37 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 30 | 0 | 1 | 1 | 2 |
| 1 | 1 | 0 | 42 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 43 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 28 | 1 | 0 | 0 | 2 |
| 0 | 1 | 1 | 29 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 51 | 1 | 0 | 1 | 2 |
| 0 | 1 | 1 | 22 | 0 | 1 | 0 | 2 |
| 1 | 1 | 0 | 40 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 28 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 52 | 0 | 1 | 1 | 2 |
| 0 | 1 | 0 | 38 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 26 | 1 | 0 | 0 | 2 |
| 0 | 0 | 1 | 33 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 26 | 1 | 0 | 0 | 2 |
| 0 | 1 | 0 | 23 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 37 | 1 | 0 | 1 | 2 |
| 0 | 0 | 1 | 50 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 24 | 0 | 1 | 0 | 2 |
- 带分类数据
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | class |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 12 | 0 | 1 | |
| 0 | 0 | 0 | 1 | 10 | 0 | 1 | |
| 1 | 0 | 0 | 0 | 24 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 27 | 1 | 0 | |
| 0 | 0 | 1 | 0 | 36 | 0 | 1 | |
| 0 | 1 | 0 | 1 | 12 | 0 | 1 | |
| 1 | 0 | 1 | 0 | 36 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 24 | 0 | 0 | |
| 0 | 1 | 0 | 0 | 48 | 0 | 0 | |
| 1 | 0 | 0 | 1 | 6 | 1 | 0 | |
| 0 | 1 | 0 | 0 | 30 | 1 | 0 | |
| 0 | 0 | 1 | 0 | 18 | 0 | 1 | |
| 0 | 1 | 0 | 1 | 18 | 1 | 0 | |
| 0 | 0 | 1 | 0 | 24 | 1 | 0 | |
| 0 | 0 | 1 | 1 | 9 | 0 | 1 | |
| 0 | 1 | 0 | 1 | 18 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 15 | 1 | 0 | |
| 0 | 1 | 0 | 1 | 24 | 1 | 0 | |
| 0 | 1 | 0 | 0 | 24 | 0 | 0 | |
| 0 | 1 | 0 | 1 | 36 | 0 | 0 |
分析
本文拟采用C4.5算法对上述的数据进行分类，开发环境：visual studio 2019，使用C/C++语言编写相关代码。
知识点
1. 信息增益比例
一个属性的增益比例1公式：
\[GainRatio(A)=\frac{Gain(A)}{SplitI(A)}\tag{1}
\]
\[SplitI(A)=-\sum_{j=1}^{v} p_j \log _2{p_j}\tag{2}
\]
上述式子的内容部分继承自ID3算法，接下来简单地介绍一下相关的知识。
- 信息增益
假设给定的数据样本集为: \(X=\{ (x_i,y_i)|i=1,2, \cdots ,total \}\)，其中样本\(x_i(i=1,2,\cdots,total)\)用d维特征向量\(x_i=(x_{i1},x_{i2},\cdots,x_{id})\) 来表示， \(x_{i1},x_{i2},\cdots,x_{id}\)分别对应d个描述属性\(A_1,A_2,\cdots,A_d\)的具体取值； \(y_i(i=1,2,\cdots,total)\)表示数据样本\(x_i\)的类标号，假设给定数据集包含m个类别，则\(y_i \in \{c_1,c_2,\cdots,c_m \}\)，其中\(c_21,c_2,\cdots,c_m\)是类别属性C的。
- 假设\(n_j\)是数据集X中属于类别\(c_j\)的样本数量，则各类别的先验概率为\(P(c_j)=\frac{n_j}{total},j=1,2,\cdots,m\)。对于给定数据集X，计算期望信息：
\[I(n_1,n_2,\cdots ,n_m)=-\sum_{j=1}^{m}P(c_j)\log _2{P(c_j)} \tag{3}
\]
- 计算描述属性Af划分数据集X所得的熵
- 假设描述属性\(A_f\)有q个不同取值，将X划分为q个子集\({X_1,X_2,\cdots,X_s,\cdots,X_q}\) ，其中\(X_s(s=1,2,\cdots,s)\)中的样本在\(A_f\)上具有相同的取值。
- 假设\(n_s\)表示\(X_s\)中的样本数量，\(n_{js}\) 表示\(X_s\)中属于类别\(c_j\)的样本数量。则由描述属性\(A_f\)划分数据集X所得的熵为：
\[E(A_f)=\sum_{s=1}^{q}\frac{n_{1s}+\cdots+n_{ms}}{total} I(n_{1s},\cdots,n_{ms}) \tag{4}
\]
其中：
\[I(n_{1s},\cdots,n_{ms})=-\sum_{j=1}^{m}p_{js}log_2{(p_{js})} \tag{5}
\]
式中的 \(p_js=\frac{n_{js}}{n_s}\)，\(p_{js}\) 表示在子集\(X_s\)中类别为\(c_j\)的数据样本所占的比例。熵值越小，表示属性对数据集划分的纯度越高。计算Af划分数据集时的信息增益：
\[Gain(A_f)=I(n_1,n_2,\cdots,n_m)-E(A_f) \tag{5}
\]
2. 合并具有连续值的属性
对于连续属性值，C4.5其处理过程如下：
- 根据属性的值，对数据集排序；
- 用不同的阈值对数据集动态地进行划分；
- 当输出改变时确定一个阈值；
- 取两个实际值中的中点作为一个阈值；
- 取两个划分，所有样本都在这两个划分中；
- 得到所有可能的阈值、增益及增益比；
- 在每一个属性会变为两个取值，即小于阈值或大于等于阈值。
简单地说，针对属性有连续数值的情况，则在训练集中可以按升序方式排列。如果属性A共有n种取值，则对每个取值\(v_j(j=1,2,\cdots,n)\)，将所有的记录进行划分：一部分小于\(v_j\)；另一部分则大于或等于\(v_j\) 。针对每个\(v_j\)计算划分对应的增益比率，选择增益最大的划分来对属性A进行离散化 。
3. 处理含有未知属性值的训练样本
C4.5处理的样本中可以含有未知属性值，其处理方法是常用的值替代或者是将最常用的值分在同一个类中。具体采用概率的方法，依据属性已知的值，对属性和每一个值赋予一个概率，取得这些概率依赖于该属性已知的值。
4. 规则的产生
一旦树被建立，就可以把树转换成if-then规则。规则存储在一个二维数组中，每一行代表树的一个规则，即从根到叶之间的一个路径。表中的每列存放树中的结点。
- 算法示例
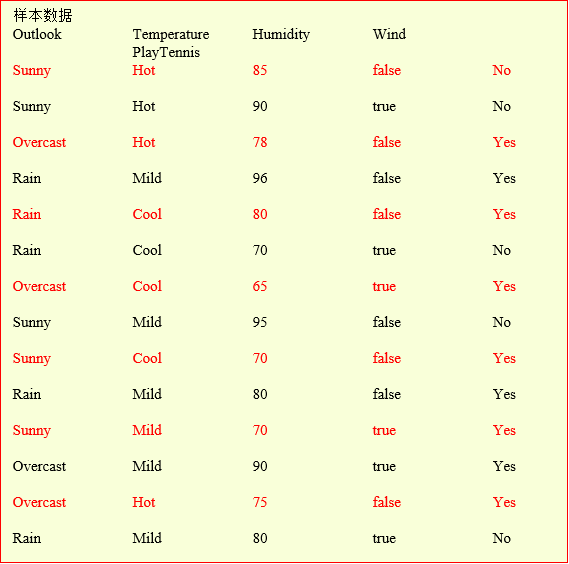
- 首先对Humidity进行属性离散化，针对上面的训练集合，通过检测每个划分而确定最好的划分在75处，则这个属性的范围就变为\({(<=75 ,>75)}\)。
- 计算目标属性PlayTennis分类的期望信息：\(I(s_1,s_2)=I(9,5)=-\frac{9}{14}\log_2{\frac{9}{14}}-\frac{5}{12}\log_2{\frac{5}{14}}=0.940\)；
- 计算每个属性的 GainRatio： $$ GainRatio(Outlook)=\frac{0.2467}{1.577}=0.156 $$ $$ GainRatio(windy)=0.049 $$ $$ GainRatio(Temperature)=0.0248 $$ $$ GainRatio(Humidity)=0.0483 $$
- 选取最大的
GainRatio，根据Outlook的取值，将三分枝。 - 再扩展各分枝节点，得到决策树。
5. 算法描述
5.1 ID3算法
1.概念提取算法CLS
1) 初始化参数C={E},E包括所有的例子,为根.
2) IF C中的任一元素e同属于同一个决策类
则创建一个叶子
节点YES终止.
ELSE 依启发式标准,选择特
Fi={V1,V2,V3,．．．Vn}并创建
判定节点
划分C为互不相交的N个集合C1,C2,C3,．．．,Cn；
3) 对任一个Ci递归.
1) 随机选择C的一个子集W (窗口).
2) 调用CLS生成W的分类树DT(强调的启发式标准在后).
3) 顺序扫描C搜集DT的意外(即由DT无法确定的例子).
4) 组合W与已发现的意外,形成新的W.
5) 重复2)到4),直到无例外为止.
-
启发式标准
只跟本身与其子树有关,采取信息理论用熵来量度. 熵是选择事件时选择自由度的量度,其计算方法为
P=freq(Cj,S)/|S|;
INFO(S)=-SUM( PLOG(P) ) ;
SUM()函数是求j从1到n和.
Gain(X)=Info(X)-Infox(X);
Infox(X)=SUM( (|Ti|/|T|)Info(X);
为保证生成的决策树最小,ID3算法在生成子树时,选取使生成的子树的熵(即Gain(S))最小的的特征来生成子树. -
ID3算法对数据的要求
- 所有属性必须为离散量.
- 所有的训练例的所有属性必须有一个明确的值.
- 相同的因素必须得到相同的结论且训练例必须唯一.
- ID3算法性能分析
- ID3算法的假设空间包含所有的决策树，它是关于现有属性的有限离散值函数的一个完整空间。所以ID3算法避免了搜索不完整假设空间的一个主要风险：假设空间可能不包含目标函数。
- ID3算法在搜索的每一步都使用当前的所有训练样例，大大降低了对个别训练样例错误的敏感性。因此，通过修改终止准则，可以容易地扩展到处理含有噪声的训练数据。
- ID3算法在搜索过程中不进行回溯。所以，它易受无回溯的爬山搜索中的常见风险影响：收敛到局部最优而不是全局最优。
- ID3算法只能处理离散值的属性。
- 信息增益度量存在一个内在偏置，它偏袒具有较多值的属性。例如，如果有一个属性为日期，那么将有大量取值，这个属性可能会有非常高的信息增益。假如它被选作树的根结点的决策属性则可能形成一颗非常宽的树，这棵树可以理想地分类训练数据，但是对于测试数据的分类性能可能会相当差。
- ID3算法增长树的每一个分支的深度，直到恰好能对训练样例完美地分类。当数据中有噪声或训练样例的数量太少时，产生的树会过渡拟合训练样例。
5.2 C4.5算法
- C4.5算法是从ID3算法演变而来，除了拥有ID3算法的功能外，C4.5算法引入了新的方法和增加了新的功能：
- 用信息增益比例的概念；
- 合并具有连续属性的值；
- 可以处理具有缺少属性值的训练样本；
- 通过使用不同的修剪技术以避免树的过度拟合；
- K交叉验证；
- 规则的产生方式等。
参考
[1] 毛国君,段立娟.数据挖掘原理与算法--3版[M].北京:清华大学出版社,2016(2020.1重印). [2] [Wikipedia](https://en.wikipedia.org/wiki/Main_Page)
【zlc】
