关联规则挖掘理论和算法
诸多的研究人员对关联规则的挖掘问题进行了大量的研究。他们的工作涉及关联规则的挖掘理论的探索、原有算法的改进和新算法的设计、并行关联规则挖掘(Quantitive Association Rule Mining)等问题。
内容提要
- 基本概念与解决方法
- 经典的频繁项目集生成算法分析
- Apriori算法的性能瓶颈问题
- Apriori的改进算法
啤酒与尿布的故事说起
在一家超市里,有一个有趣的现象:尿布和啤酒赫然摆在一起出售。但是这个奇怪的举措却使尿布和啤酒的销量双双增加了。这不是一个笑话,而是发生在美国沃尔玛连锁店超市的真实案例,并一直为商家所津津乐道。沃尔玛拥有世界上最大的数据仓库系统,为了能够准确了解顾客在其门店的购买习惯,沃尔玛对其顾客的购物行为进行购物篮分析,想知道顾客经常一起购买的商品有哪些。沃尔玛数据仓库里集中了其各门店的详细原始交易数据。在这些原始交易数据的基础上,沃尔玛利用数据挖掘方法对这些数据进行分析和挖掘。一个意外的发现是:"跟尿布一起购买最多的商品竟是啤酒!经过大量实际调查和分析,揭示了一个隐藏在"尿布与啤酒"背后的美国人的一种行为模式:在美国,一些年轻的父亲下班后经常要到超市去买婴儿尿布,而他们中有30%~40%的人同时也为自己买一些啤酒。产生这一现象的原因是:美国的太太们常叮嘱她们的丈夫下班后为小孩买尿布,而丈夫们在买尿布后又随手带回了他们喜欢的啤酒。

概述
关联规则(Association Rule Mining)挖掘是数据挖掘中最活跃的研究方法之一 最早是由R.Agrawal等人提出的 其目的是为了发现超市交易数据库中不同商品之间的关联关系。 一个典型的关联规则的例子是:70%购买了牛奶的顾客将倾向于同时购买面包。 经典的关联规则挖掘算法:Apriori算法和FP-growth算法
引例
假定某超市销售的商品包括:bread、bear、cake、cream、milk和tea

定义3.1 项目与项集:设I={i1,i2,…,im}是m个不同项目的集合,每个ik(k=1,2,……,m)称为一个项目(Item)。项目的集合I称为项目集合(Itemset),简称为项集。其元素个数称为项集的长度,长度为k的项集称为k-项集(k-Itemset)。
定义3.2 交易:每笔交易T(Transaction)是项集I上的一个子集,即 \( T\subseteq I \),但通常 \( T \subset I \)。对应每一个交易有一个唯一的标识——交易号,记作TID。交易的全体构成了交易数据库D,或称交易记录集D,简称交易集D。交易集D中包含交易的个数记为|D|。
定义3.3 项集的支持度:对于项集X,\( X \subset I \),设定count( \( X\subseteq T \) )为交易集D中包含X的交易的数量。项集X的支持度support(X)就是项集X出现的概率,从而描述了X的重要性。
\begin{equation}
support(X)=\frac{count(X \subseteq T)}{ |D| }
\end{equation}
定义3.4 项集的最小支持度与频繁集:发现关联规则要求项集必须满足的最小支持阈值,称为项集的最小支持度(Minimum Support),记为supmin。从统计意义上讲,它表示用户关心的关联规则必须满足的最低重要性。只有满足最小支持度的项集才能产生关联规则。支持度大于或等于supmin的项集称为频繁项集,简称频繁集,反之则称为非频繁集。通常k-项集如果满足supmin,称为k-频繁集,记作Lk。
定义3.5 关联规则:关联规则(Association Rule)可以表示为一个蕴含式:\( R:X\Rightarrow Y \)
定义3.6 关联规则的支持度:对于关联规则 \( R:X\Rightarrow Y \),其中\( X\subset I \),\( Y\subset I \),并且\(X\cap Y=\Phi \),规则R的的支持度(Support)是交易集中同时包含X和Y的:易数与所有交易数之比。
\begin{equation}
support(X \Rightarrow Y)=\frac{count(X \cup Y)}{|D|}
\end{equation}
定义3.7 关联规则的可信度:对于关联规则 \( R:X\Rightarrow Y \),其中\( X\subset I \),\( Y\subset I \),并且\(X\cap Y=\Phi \),规则R的可信度(Confidence)是指包含X和Y的交易数与包含X的交易数之比
\begin{equation}
support(X \Rightarrow Y)=\frac{count(X \cup Y)}{support(X)}
\end{equation}
定义3.8 关联规则的最小支持度和最小可信度:关联规则的最小支持度也就是衡量频繁集的最小支持度(Minimum Support),记为supmin,它用于衡量规则需要满足的最低重要性。规则的最小可信度(Minimum Confidence)记为confmin,它表示关联规则需要满足的最低可靠性。
简单例子如下:
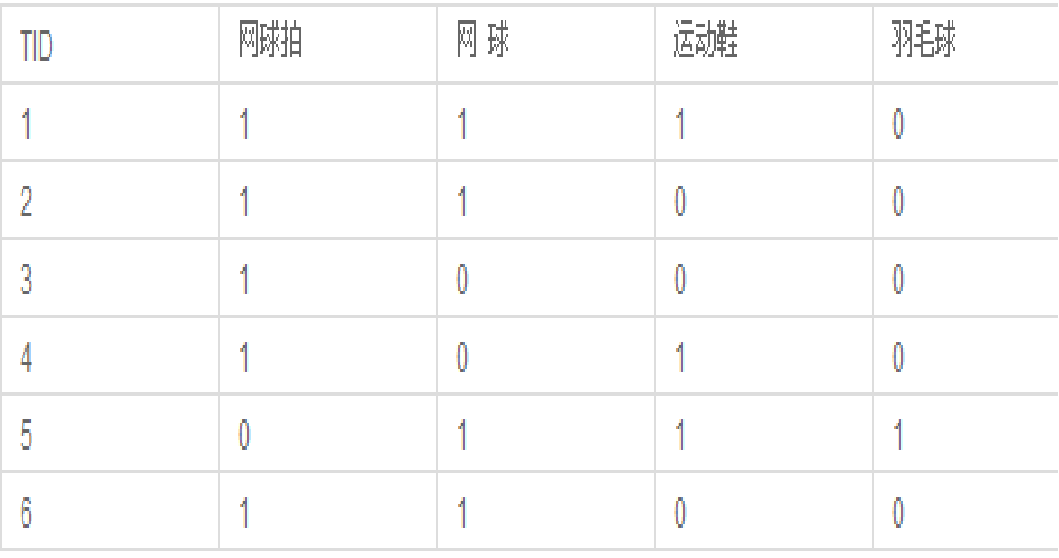
顾客购买记录的数据库D,包含6个事务。项集I={网球拍,网球,运动鞋,羽毛球}。考虑关联规则(频繁二项集):网球拍与网球,事务1,2,3,4,6包含网球拍,事务1,2,6同时包含网球拍和网球,支持度(X^Y)/D=0.5,置信度(X^Y)/X=0.6。若给定最小支持度α = 0.5,最小置信度β = 0.6,认为购买网球拍和购买网球之间存在关联。
定义3.9 强关联规则:如果规则 \( X\Rightarrow Y \)满足:\( support(X\Rightarrow Y) \ge supmin \) 且\( confidence(X \Rightarrow Y) \ge confmin \),称关联规则 \( X \Rightarrow Y \)为强关联规则,否则称关联规则 \( X\Rightarrow Y \)为弱关联规则。在挖掘关联规则时,产生的关联规则要经过supmin和confmin的衡量,筛选出来的强关联规则才能用于指导商家的决策。
关联规则挖掘问题可以划分成两个子问题: 1. 发现频繁项目集:通过用户给定Minsupport ,寻找所有频繁项目集或者最大频繁项目集。 2.生成关联规则:通过用户给定Minconfidence ,在频繁项目集中,寻找关联规则。 第1个子问题是近年来关联规则挖掘算法研究的重点。
经典的频繁项目集生成算法分析:项目集空间理论、经典的发现频繁项目集算法、关联规则生成算法。Agrawal等人建立了用于事务数据库挖掘的项目集格空间理论(1993, Appriori 属性)。
定理3-1( Appriori 属性1):如果项目集X 是频繁项目集,那么它的所有非空子集都是频繁项目集。 证明 设X是一个项目集,事务数据库T 中支持X 的元组数为s。对X的任一非空子集为Y,设T中支持Y的元组数为 \( s_1 \) 。 根据项目集支持数的定义,很容易知道支持X 的元组一定支持Y,所以 \( s_1 \ge s \) ,即 \( support(Y) \ge support(X) \)。 按假设:项目集X 是频繁项目集,即\( support(Y) \ge minsupport \), 所以 \( support(Y) \ge support(X) \ge minsupport \),因此Y是频繁项目集。□
定理3-2( Appriori 属性2):如果项目集X 是非频繁项目集,那么它的所有超集都是非频繁项目集。 证明 (略)
算法3-1 Apriori(发现频繁项目集)1994年,Agrawal 等人提出了著名的Apriori 算法。

算法apriori中调用了apriori-gen( \( L_{k-1} \)),是为了通过(k-1)-频集产生K-侯选集。

has_infrequent_subset(c, \( L_{k-1} \) ),判断c是否加入到k-侯选集中。发现算法解决的是关联规则挖掘的第一个问题。关联规则分为布尔关联规则和多值规则。多值关联规则都转化为布尔关联规则来解决,因此先介绍布尔关联规则算法 Apriori,AprioriTid。分为第一次遍历和第k次遍历。第一次遍历计算每个项目的具体值,确定大项目集1项目集 \( L_1 \)。第k次遍历利用前一次找到的大项集 \( L_{k-1} \) 和Apriori-gen函数产生候选集 \( C_k \) ,然后扫描数据库,得到 \( C_k \) 中候选的支持度,剔除了不合格的候选后 \( C_k \) 作为\( L_k \) 。下表给出一个样本事务数据库,并对它实施Apriori算法。

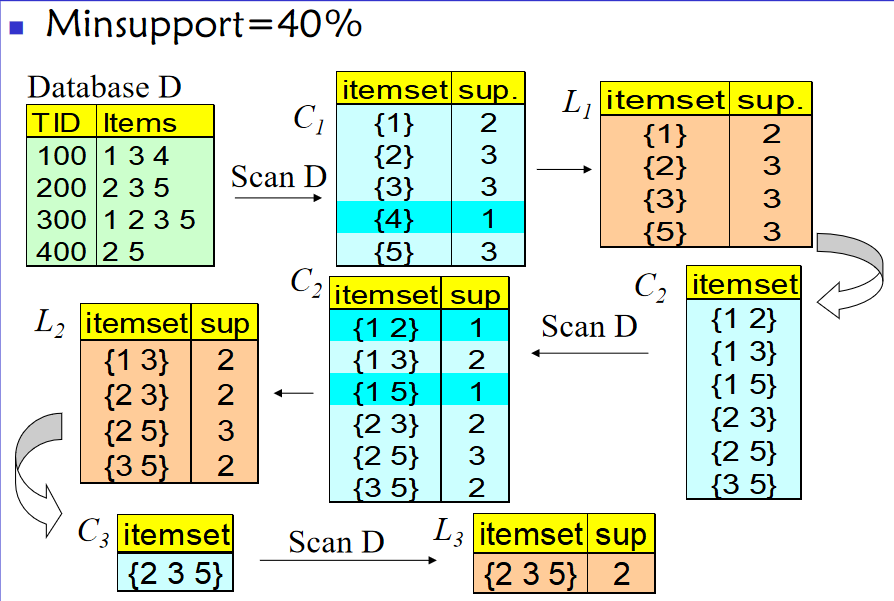
根据上面介绍的关联规则挖掘的两个步骤,在得到了所有频繁项目集后,可以按照下面的步骤生成关联规则: 对于每一个频繁项目集l,生成其所有的非空子集; 对于l 的每一个非空子集x,计算Conference(x),如果 \( Confidence(x) \ge minconfidence \) ,那么“ \( x \Rightarrow (1-x) \) ”成立。
算法3-4 从给定的频繁项目集中生成强关联规则,核心是genrules递归过程,它实现一个频繁项目集中所有强关联规则的生成。

算法3-5 递归测试一个频集中的关联规则

Minconfidence=80%
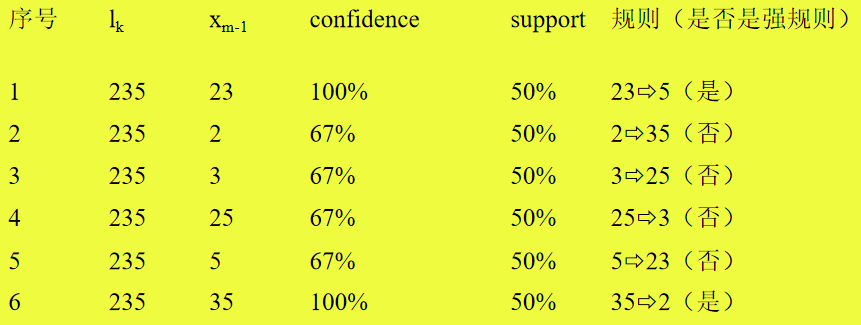
Apriori作为经典的频繁项目集生成算法,在数据挖掘中具有里程碑的作用。
Apriori算法有两个致命的性能瓶颈: 1.多次扫描事务数据库,需要很大的I/O负载 对每次k循环,侯选集 \( C_k \) 中的每个元素都必须通过扫描数据库一次来验证其是否加入\( L_k \) 。假如有一个频繁大项目集包含10个项的话,那么就至少需要扫描事务数据库10遍。 2.可能产生庞大的侯选集 由\( L_k -1 \) 产生k-侯选集 \( C_k \) 是指数增长的,例如 \( 10^4 \) 个1-频繁项目集就有可能产生接近 \( 10^7 \) 个元素的2-侯选集。如此大的侯选集对时间和主存空间都是一种挑战。
Apriori的改进算法:基于数据分割的方法、基于散列的方法。一些算法虽然仍然遵循Apriori 属性,但是由于引入了相关技术,在一定程度上改善了Apriori算法适应性和效率。 主要的改进方法有: 基于数据分割(Partition)的方法:基本原理是“在一个划分中的支持度小于最小支持度的k-项集不可能是全局频繁的”。 基于散列(Hash)的方法:基本原理是“在一个hash桶内支持度小于最小支持度的k-项集不可能是全局频繁的”。 基于采样(Sampling)的方法:基本原理是“通过采样技术,评估被采样的子集中,并依次来估计k-项集的全局频度”。 其他:如,动态删除没有用的事务:“不包含任何Lk的事务对未来的扫描结果不会产生影响,因而可以删除”。
定理3-5:设数据集D被分割成分块 \( D_1,D_2, \cdots , D_n \) ,全局最小支持数为minsup_count。如果一个数据分块 \( D_i \) 的局部最小支持数minsup_coun \( t_i (i=1,2, \cdots, n) \),按着如下方法生成: minsup_coun \( t_i \) = minsup_count *|| \( D_i \) || / ||D|| 则所有的局部频繁项目集涵盖全局频繁项目集。 作用:
1.合理利用主存空间:数据分割将大数据集分成小的块,为块内数据一次性导入主存提供机会。
2.支持并行挖掘算法:每个分块的局部频繁项目集是独立生成的,因此提供了开发并行数据挖掘算法的良好机制。
1995,Park等发现寻找频繁项目集的主要计算是在生成2-频繁项目集上。因此,Park等利用了这个性质引入杂凑技术来改进产生2-频繁项目集的方法。例子:桶地址 =(10x+y)mod 7;minsupport_count=3

对项目集格空间理论的发展 Close算法 FP-tree算法。随着数据库容量的增大,重复访问数据库(外存)将导致性能低下。因此,探索新的理论和算法来减少数据库的扫描次数和侯选集空间占用,已经成为近年来关联规则挖掘研究的热点之一。 两个典型的方法: Close算法 FP-tree算法。一个频繁闭合项目集的所有闭合子集一定是频繁的;一个非频繁闭合项目集的所有闭合超集一定是非频繁的。 什么是一个闭合的项目集? 一个项目集C是闭合的,当且仅当对于在C中的任何元素,不可能在C中存在小于或等于它的支持度的子集。 例如,C1={AB3,ABC2}是闭合的; C2={AB2,ABC2}不是闭合的;下面是Close算法作用到表4-1数据集的执行过程(假如minsup_count=3):

扫描数据库得到 \( L_1 \) ={(A,3), (B,5), (C,4), (D,3), (E,3)};相应关闭项目集为 \( C_1 \) (A)={ABC,3}, \( C_1 \) (B)={B,5}, \( C_1 \) (C)={BC,4}, \( C_1 \) (D)={BD,3}, \( C_1 \) (E)={BE,3} ; \( L_2 \) ={(AB,3), (AC,3), (BC,4), (BD,3), (BE,3)};相应关闭集为 \( C_2 \) (AB)={ABC,3}; \( L_3 \) , \( L_4 \) , \( L_5 \) 不用测,于是频繁大项集为{ABC }。
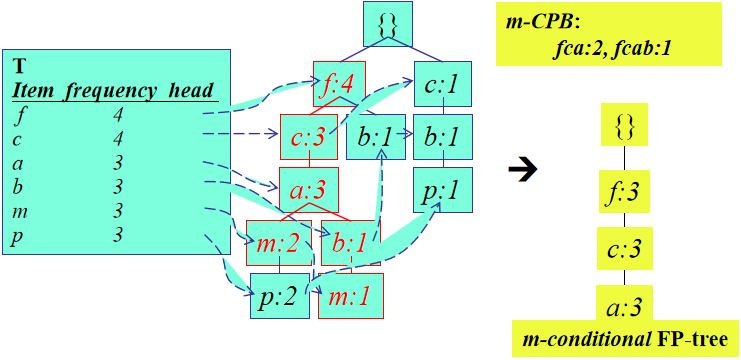
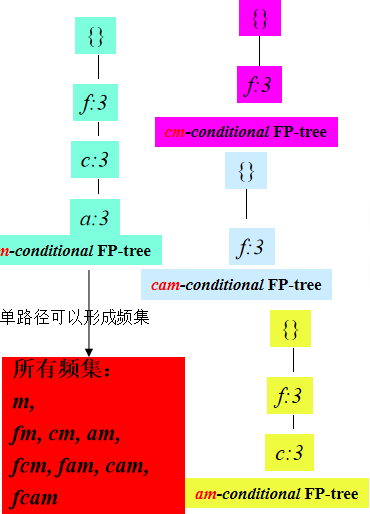
FP-tree算法的基本原理:进行2次数据库扫描,一次对所有1-项目的频度排序;一次将数据库信息转变成紧缩内存结构。 不使用侯选集,直接压缩数据库成一个频繁模式树,通过频繁模式树可以直接得到频集。 基本步骤是: 两次扫描数据库,生成频繁模式树FP-Tree: 扫描数据库一次,得到所有1-项目的频度排序表T; 依照T,再扫描数据库,得到FP-Tree。 使用FP-Tree,生成频集: 为FP-tree中的每个节点生成条件模式库; 用条件模式库构造对应的条件FP-tree; 递归挖掘条件FP-trees同时增长其包含的频繁集: 如果条件FP-tree只包含一个路径,则直接生成所包含的频繁集。

为每个节点, 寻找它的所有前缀路径并记录其频度,形成CPB
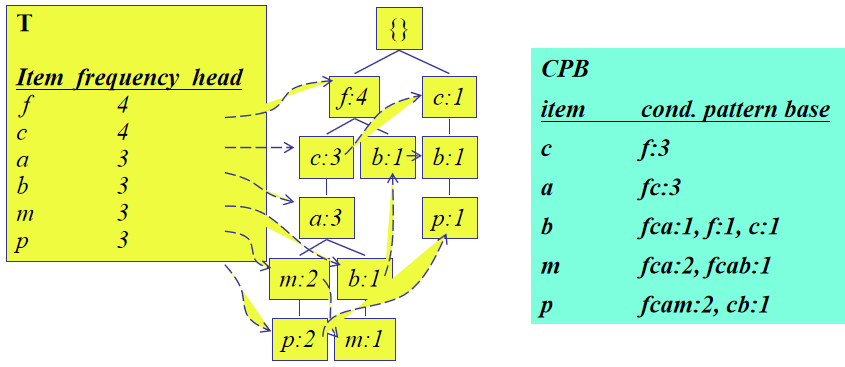
为每一个节点,通过FP-tree构造一个C-FP-tree。例如,m节点的C-FP-tree为:
实验内容
1.用你自己熟悉的语言,编写程序(Apriori算法,Close算法,FP-tree 算法中的一种)对所给定的数据集进行关联规则挖掘,给出具体程序和挖掘结果,结果要求包含频繁项集与强关联规则。
2.最小支持度与最小可信度自行设定(要求给出调整过程),从而得出合理的最小支持度与最小可信度。


 关联规则挖掘是数据挖掘中最活跃的研究方法之一。最早是有Agrawal 等人提出的(1993)。最初的动机是针对购物篮分析(Basket Analysis)问题提出的,其目的是为了发现交易数据库(Transaction Database)中不同商品之间的联系规则。这些规则刻画了顾客购买行为模式,可以用来指导商家科学地安排进货、库存以及货架设计的步等。关联规则在其他领域也可以得到广泛的讨论。例如,医学研究人员希望从已有的成千上万份病历中找出患某种疾病的病人的共同特征,从而为治愈这种疾病提供一些帮助。
关联规则挖掘是数据挖掘中最活跃的研究方法之一。最早是有Agrawal 等人提出的(1993)。最初的动机是针对购物篮分析(Basket Analysis)问题提出的,其目的是为了发现交易数据库(Transaction Database)中不同商品之间的联系规则。这些规则刻画了顾客购买行为模式,可以用来指导商家科学地安排进货、库存以及货架设计的步等。关联规则在其他领域也可以得到广泛的讨论。例如,医学研究人员希望从已有的成千上万份病历中找出患某种疾病的病人的共同特征,从而为治愈这种疾病提供一些帮助。
