JPEG基本系统

　　JPEG标准主要采用了基于块的DCT变换编码，同时综合应用了游程编码和霍夫曼编码等。其有损压缩算法编码的大致流程如下：第一步，对图像块（把整个图像分成多个 \( 8 \times 8 \) 子块）进行DCT变换，得到DCT系数；第二步，根据量化表对DCT系数进行量化；第三步，对DCT系数中的直流（DC）系数进行差分预测，对交流（AC）系数按Zig-Zig顺序重新排序；第四步，对第三步得到的系数进行霍夫曼编码。

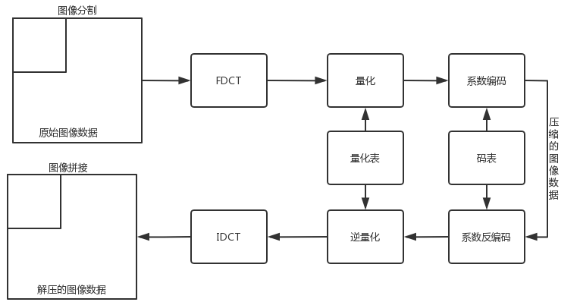
图1　　JPEG基本系统框图

　　1. FDCT和IDCT：JPEG基本系统以DCT变换为基础，采用固定的 \( 8 \times 8 \) 子块。其表达式如下：

\begin{equation}
F(u,v)=C(u)C(v)\sum_{i=0}^{7}\sum_{j=0}^{7}f(i,j)
\cos{\left [ \frac{(2i+1)u\pi }{16} \right ] }
\cos{\left [ \frac{(2j+1)v\pi }{16} \right ] }
\end{equation}

\begin{equation}
f(i,j)=\sum_{i=0}^{7}\sum_{j=0}^{7}F(u,v)C(u)C(v)
\cos{\left [ \frac{(2i+1)u\pi }{16} \right ] }
\cos{\left [ \frac{(2j+1)v\pi }{16} \right ] }
\end{equation}

\begin{equation}
C(u),C(v)=\left\{\begin{matrix}
1/ \sqrt{2} & u,v=0 \\
1 & other
\end{matrix}\right.
\end{equation}

　　在JPEG基本系统中，\( f(x,y) \) 为8bit 像素，即取值范围为 \( 0\sim 255 \) ，由DCT变换可求得DC系数 \( F(0,0) \) 的取值范围为 \( 0 \sim 2040 \) ,实际上，同样可以求出 \( F(0,0) \) 是图像均值的8倍，除   \( F(0,0) \) 外的其他系数为AC系数。

　　2. 量化与逆量化：对低频系数缩小，对高频系数放大，是大部分幅值较小的系数在量化后变为0，然后只剩下一小部分系数需要存储，从而大大压缩了数据量。量化的过程就是每个DCT系数除以各自的量化步长并取整，然后得到量化后的系数：

\begin{equation}
\tilde{F}(u,v)=INT\left [ \frac{F(u,v)}{S(u,v)} \pm 0.5 \right ]
\end{equation}

　　人眼视觉系统的频率频率响应，随着空间频率的增加而下降，且对于色度分量的下降比亮度分量要快。为此，JPEG为亮度分量和色度分量分别推荐了量化表如下：

　　亮度量化表：

16	11	10	16	24	40	51	61
12	12	14	19	26	58	60	55
14	13	16	24	40	57	69	56
14	17	22	29	51	87	80	62
18	22	37	56	68	109	103	77
24	35	55	64	81	104	113	92
49	64	78	87	103	121	120	101
72	92	95	98	112	100	103	99

　　色度量化表

17	18	24	47	99	99	99	99
18	21	26	66	99	99	99	99
24	26	56	99	99	99	99	99
47	66	99	99	99	99	99	99
99	99	99	99	99	99	99	99
99	99	99	99	99	99	99	99
99	99	99	99	99	99	99	99
99	99	99	99	99	99	99	99

\begin{tabular}{|c|c|c|c|c|c|c|}

    \hline

    \multirow{2}{*}{Method}&

    \multicolumn{3}{c|}{C}&\multicolumn{3}{c|}{ D}\cr\cline{2-7}

    &Precision&Recall&F1-Measure&Precision&Recall&F1-Measure\cr

    \hline

    \hline

    A&0.7324&0.7388&0.7301&0.6371&0.6462&0.6568\cr\hline

   B&0.7321&0.7385&0.7323&0.6363&0.6462&0.6559\cr\hline

    C&0.7321&0.7222&0.7311&0.6243&0.6227&0.6570\cr\hline

    D&0.7654&0.7716&0.7699&0.6695&0.6684&0.6642\cr\hline

    E&0.7435&0.7317&0.7343&0.6386&0.6488&0.6435\cr\hline

    F&0.7667&0.7644&0.7646&0.6609&0.6687&0.6574\cr\hline

    G&{\bf 0.8189}&{\bf 0.8139}&{\bf 0.8146}&{\bf 0.6971}&{\bf 0.6904}&{\bf 0.6935}\cr

    \hline

    \end{tabular}

　　3. 对量化系数编码：对于由量化器输出的量化系数，JPEG采用定长和变长相结合的编码方法，具体如下：

　　（1）直流（DC）系数，由于图像中相邻的两个图像块的DC系数一般很接近，所以JPEG对量化后的系数采用无失真DPCM编码，即对当前块的DC系数 \( F_i(0,0) \) 和已编码的相邻块DC系数\( F_{i-1}(0,0) \) 的差值进行编码。

\begin{equation}
\Delta F(0,0)=F_i(0,0)-F_{i-1}(0,0)
\end{equation}

　　按照其取值范围，JPEG将差值分为12类。编码时，将DC系数差值表示为“符号1 符号2”的形式，其中符号1为从表中查得的类别，实际上就是用自然二进制码表示DC系数差值所需的最少比特数，符号2为实际的差值。对符号1，即DC系数差值的类别，采用霍夫曼编码。由于亮度和色度分量的DC系数差值统计特性差别较大，所以JPEG为两者分别推荐了霍夫曼表。对符号2，采用二进制码，负数用整数的反码表示。例如：差值为2，用于“10”表示；差值为-2，用“01”表示。

类别	取值	类别	取值
0	0	6	-63~-32,32~63
1	-1,1	7	-127~-64,64~127
2	-3，-2,2,3	8	-255~-128,128~255
3	-7~-4,4~7	9	-511~-256,256~511
4	-15~-8,8~15	10	-1023~-512,512~1023
5	-31~-16,16~31	11	-2047~-1024,1024~2047

 　　2.交流（AC）系数：Z型扫描（系数的重新排列）：因为经过量化以后，AC系数中出现较多的0，所以JPEG采用对0系数的游程长度编码，即将所有AC系数表示为 \( 00\cdots 0X,00\cdots 0X,\cdots ,00\cdots 0X,\cdots  \)，其中，X表示非0值。若干个0和一个非0值X组成一个编码的基本单位，连续零的个数越多，编码效率就越高。因此，根据DCT系数量化后的分布特点，对DCT系数采取如图所示的Z型扫描方式，以使大多数出现在右下角的0能够连起来，出现更多的连0。熵编码：对于连0，可以用其游程即个数表示。同DC系数差值编码类似JPEG

 

1.