船舶运动控制器及仿真程序
将船舶视为刚体,其动力学在平衡点经3阶展开如下式所示
\begin{equation}
\left[\begin{array}{ccc}
m-X_{i} & 0 & 0 \\
0 & m-X_{i} & m x_{g}-Y_{i} \\
0 & m x_{g}-N_{i} & I_{z}-N_{\dot{r}}
\end{array}\right]
\left[\begin{array}{c}\Delta \dot{u} \\
\dot{v} \\
\dot{r}
\end{array}\right] = \left[\begin{array}{c}
X \\
Y \\
N
\end{array}\right]
\end{equation}
\begin{equation}
\left\{\begin{matrix}
X= & X_{u} \Delta u +X_{uu} \Delta u^2+X_{uu} \Delta u^3+X_{vv} \Delta v^2+X_{rr} \Delta r^2 + X_{rv} rv\\
&+ X_{\delta \delta } \Delta \delta ^2 + X_{u\delta \delta } \Delta u \delta ^2 + X_{v \delta } v \delta+ X_{uv \delta } \Delta uv \delta \quad \quad \quad \quad \quad \quad \\
Y= & Y_{v} v +Y_{r} r+Y_{vvv} v^3+Y_{vvr} rv^2+Y_{vu} \Delta u + Y_{ru} r\Delta u \qquad \qquad \\
&+ Y_{\delta} \Delta + Y_{\delta \delta \delta } \delta ^3 + Y_{u \delta } \Delta u \delta+ Y_{uu \delta } \Delta u^2 \delta +Y_{v\delta \delta } v\delta ^2+Y_{vv\delta } v^2\delta \\
N= & N_{v} \Delta v +N_{r} \Delta r+N_{vvv} \Delta v^3+N_{vu} v\Delta u+N_{ru} r\Delta u + N_{\delta } \delta \qquad \\
&+ N_{\delta \delta \delta } \Delta \delta ^3 + N_{u\delta } \Delta u \delta + N_{uu \delta } \Delta u^2 \delta+ N_{v \delta \delta } v \delta ^2 +N_{vv\delta } v^2\delta \quad
\end{matrix}\right.
\end{equation}
式中 \( [\Delta u \quad v \quad r] \) 分别表示纵向速度偏差、横漂速度偏差和舵向速度偏差,\( \Delta u = u-U_0 \) ,\( \Delta v = v \) ,\( \Delta r = r \) ,\( U_0 \) 为经济航速,m为质量, \( I_z \) 为转动惯量,\( x_g \) 为中心中心矩 \( [X \quad Y \quad N] \) 为舵力, \( X_u \), \( X_{uu} \),\( Y_v \),\( N_v \)等是动力学泰勒展开时的系数。船舶动力学方程如下:
\begin{equation}
\left\{\begin{matrix}
\dot{x} = u\cos \psi - v\sin \psi +U_c\cos \gamma _c \\
\dot{y} = u\sin \psi - v\cos \psi +U_c\sin \gamma _c \\
\dot{\psi } = r \qquad \qquad \qquad \qquad \qquad \quad\\
\dot{\delta } = \dot{\delta } \qquad \qquad \qquad \qquad \qquad \quad
\end{matrix}\right.
\end{equation}
式中, \( \psi \) 为偏航角, \( U_c \) 为流速, \( \gamma_c \) 为流向,\( x \)为北向坐标,\( y \)为东向坐标, \( \delta \) 为舵偏角。控制器方程式如式
\begin{equation}
\delta =
\left\{\begin{matrix}
\left | \delta \right | < \delta _{max} & -K\left ( \left ( \psi -\psi _0 \right ) + T_d \times r \right ) \\
\left | \delta \right | > \delta _{max} & \delta _{max},-\delta _{max}
\end{matrix}\right.
\end{equation}
式中 \( \delta \) 为舵偏角, \( \delta_{max} \) 为允许的最大舵偏角, \( K_p \) 为PD控制器P增益,T_d为PD控制器D增益,\( \psi_0 \) 为目标偏航角。船舶控制逻辑为:通过控制舵偏角使得船舶偏航角达到指定角度,控制器采用PD算法。

% 主函数,文件名为boat_PD t_f = 600; % 仿真事件设定 h = 0.1; % 采样时间 Kp = 1; % 控制器P增益 Td = 10; % 控制器D增益 % 状态x = [ u v r x y psi delta ]' 赋初值 x = zeros(7,1); N = round(t_f/h); % 采样量 xout = zeros(N+1,length(x)+2); % 输出变量赋初值 % 分支结构流程控制 for i=1:N+1, time = (i-1)*h; r = x(3); psi = x(6); psi_ref = 5*(pi/180); % 控制目标角度 delta = -Kp*((psi-psi_ref)+Td*r); % PD控制器 % 调用M函数文件 [xdot,U] = mariner(x,delta); % 船舶模型 % 存储数据以便后续调用 xout(i,:) = [time,x',U]; % 数值积分,欧拉算法 x = x + h*xdot end % 从存储的数据中给变量赋值 t = xout(:,1); u = xout(:,2); v = xout(:,3); r = xout(:,4)*180/pi; % pi为Matlab特殊常量,表示圆周率 x = xout(:,5); y = xout(:,6); psi = xout(:,7)*180/pi; delta = xout(:,8)*180/pi; U = xout(:,9); % 作图 % 如果要作多个图,用figure(i),i = 1,2,3,…来实现 figure(1) % 作完图之后,利用axis,xlabel等来丰富和定制图形的信息 plot(y,x),grid,axis('equal'),xlabel('East'),ylabel('North'),title('Ship position') figure(2) % 如果要求在一个图中作多个小图,用subplot来完成 subplot(221),plot(t,r),xlabel('time (s)'),title('yaw rate r (deg/s)'),grid subplot(222),plot(t,U),xlabel('time (s)'),title('speed U (m/s)'),grid subplot(223),plot(t,psi),xlabel('time (s)'),title('yaw angle \psi (deg)'),grid subplot(224),plot(t,delta),xlabel('time (s)'),title('rudder angle \delta (deg)'),grid

function [xdot,U] = mariner(x,ui,U0) % [xdot, U] = mariner(x,ui) 返回真实速度U in m/s 以及状态变量x = [ u v r x y psi delta n ]' %的偏差 % %输入变量有: % u = 与常规速度Uo之间的偏差,U0默认值为U0 = 7.7175 m/s = 15 knots. % v = 摇摆速度与0之间的偏差 (m/s) % r = 偏航角速度与0之间的偏差 (rad/s) % x = x方向的位置 (m) % y = y方向的位置 (m) % psi = 偏航角与0之间的偏差 (rad) % delta = 真实的舵偏角 (rad) % ui = 控制舵角指令(rad),即控制器输出 % U0 = 常规速度 (m/s) % 输出变量 % xdot为状态变量的微分 % U = 真实速度 (m/s) % 确认输入值是否符合要求 % 如果输入不是7维,则输出错误信息 if (length(x) ~= 7),error('x-vector must have dimension 7 !'); end % 如果控制舵角指令不是1维,则输出错误信息 if (length(ui) ~= 1),error('ui must be a scalar input!'); end % 如果没有输入U0信息,则采用默认值 if nargin==2, U0 = 7.7175; end % 对变量赋值及归一化 L = 160.93; U = sqrt((U0 + x(1))^2 + x(2)^2); % 真实速度 delta_c = -ui; u = x(1)/U; v = x(2)/U; r = x(3)*L/U; psi = x(6); delta = x(7); delta_max = 40; % 最大舵角 (deg) Ddelta_max = 5; % 最大舵角速度 (deg/s) m = 798e-5; Iz = 39.2e-5; xG = -0.023; % 舵力及力矩在0值附近展开系数赋值 Xudot = -42e-5; Yvdot = -748e-5; Nvdot = 4.646e-5; Xu = -184e-5; Yrdot =-9.354e-5; Nrdot = -43.8e-5; Xuu = -110e-5; Yv = -1160e-5; Nv = -264e-5; Xuuu = -215e-5; Yr = -499e-5; Nr = -166e-5; Xvv = -899e-5; Yvvv = -8078e-5; Nvvv = 1636e-5; Xrr = 18e-5; Yvvr = 15356e-5; Nvvr = -5483e-5; Xdd = -95e-5; Yvu = -1160e-5; Nvu = -264e-5; Xudd = -190e-5; Yru = -499e-5; Nru = -166e-5; Xrv = 798e-5; Yd = 278e-5; Nd = -139e-5; Xvd = 93e-5; Yddd = -90e-5; Nddd = 45e-5; Xuvd = 93e-5; Yud = 556e-5; Nud = -278e-5; Yuud = 278e-5; Nuud = -139e-5; Yvdd = -4e-5; Nvdd = 13e-5; Yvvd = 1190e-5; Nvvd = -489e-5; Y0 = -4e-5; N0 = 3e-5; Y0u = -8e-5; N0u = 6e-5; Y0uu = -4e-5; N0uu = 3e-5; % 等式(1-1)左边变量 m11 = m-Xudot; m22 = m-Yvdot; m23 = m*xG-Yrdot; m32 = m*xG-Nvdot; m33 = Iz-Nrdot; % M文件流程控制中的分支结构 if abs(delta_c) >= delta_max*pi/180, % 如果计算得舵角大于舵角允许最大值,则采用舵角允许最大值 delta_c = sign(delta_c)*delta_max*pi/180; end % 舵角速度等于现在的舵角值减去上次舵角值 delta_dot = delta_c - delta; if abs(delta_dot) >= Ddelta_max*pi/180, % 如果计算得舵角速度大于舵角速度允许最大值,则采用舵角速度允许最大值 delta_dot = sign(delta_dot)*Ddelta_max*pi/180; end % 等式(1-2) X = Xu*u + Xuu*u^2 + Xuuu*u^3 + Xvv*v^2 + Xrr*r^2 + Xrv*r*v + Xdd*delta^2 +... Xudd*u*delta^2 + Xvd*v*delta + Xuvd*u*v*delta; Y = Yv*v + Yr*r + Yvvv*v^3 + Yvvr*v^2*r + Yvu*v*u + Yru*r*u + Yd*delta + ... Yddd*delta^3 + Yud*u*delta + Yuud*u^2*delta + Yvdd*v*delta^2 + ... Yvvd*v^2*delta + (Y0 + Y0u*u + Y0uu*u^2); N = Nv*v + Nr*r + Nvvv*v^3 + Nvvr*v^2*r + Nvu*v*u + Nru*r*u + Nd*delta + ... Nddd*delta^3 + Nud*u*delta + Nuud*u^2*delta + Nvdd*v*delta^2 + ... Nvvd*v^2*delta + (N0 + N0u*u + N0uu*u^2); detM22 = m22*m33-m23*m32; % 分量计算 xdot = [ X*(U^2/L)/m11 -(-m33*Y+m23*N)*(U^2/L)/detM22 (-m32*Y+m22*N)*(U^2/L^2)/detM22 (cos(psi)*(U0/U+u)-sin(psi)*v)*U (sin(psi)*(U0/U+u)+cos(psi)*v)*U r*(U/L) delta_dot ];
仿真结果如下:
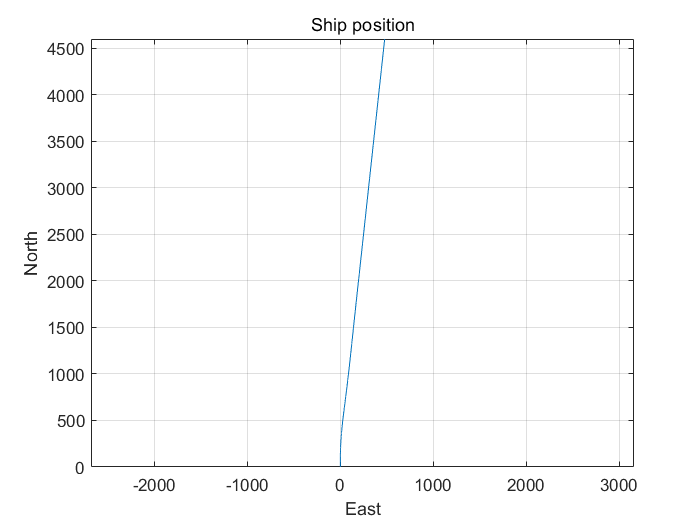
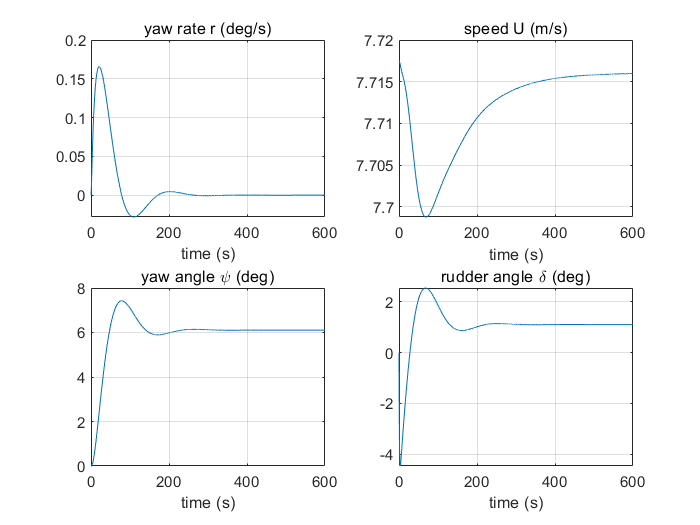
由图可看出,设计的控制器能够使船舶偏航角达到的指定角,控制器是有效的。
参考文献
[1] 施梨.MATLAB工程仿真与应用30例[M].北京:电子工业出版社,2015.5.


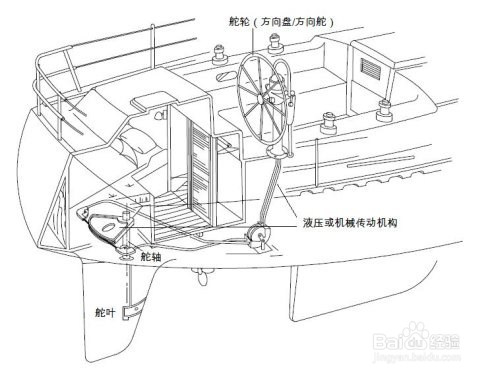 在广州出土的东汉陶船,据今已近两千年,在其尾部正中位置上已经有了舵,这个舵比操纵桨桨叶的面积宽展很多,还残留着以桨代舵的痕迹。但从世界范围来说,它是最早的舵,到了12世纪末,相当于我国南宋时期,在西方教堂的雕刻上才出现了欧洲最早的舵。
在广州出土的东汉陶船,据今已近两千年,在其尾部正中位置上已经有了舵,这个舵比操纵桨桨叶的面积宽展很多,还残留着以桨代舵的痕迹。但从世界范围来说,它是最早的舵,到了12世纪末,相当于我国南宋时期,在西方教堂的雕刻上才出现了欧洲最早的舵。

