离散傅里叶变换（OpenCV4）
图像变换是许多图像处理技术的基础，为了有效和快速地对图像进行处理和分析，常常需要将原定义在图像空间的图像以某种形式转换到另外一个空间，并利用这些空间的特有性质更方便地进行一些处理，最后再变换为图像空间以得到所需效果。近年来，众多的图像变换方法不断涌现，从古老的傅里叶变换到余弦变换，直至小波变换，这些数学模型都对图像处理技术的发展有着不可磨灭的贡献。本篇随笔主要介绍离散傅里叶变换（关于傅里叶变换原理的更加详尽的介绍请看《傅里叶变换与图像处理》）。
图像变换是许多图像处理技术的基础，为了有效和快速地对图像进行处理和分析，常常需要将原定义在图像空间的图像以某种形式转换到另外一个空间，并利用这些空间的特有性质更方便地进行一些处理，最后再变换为图像空间以得到所需效果。近年来，众多的图像变换方法不断涌现，从古老的傅里叶变换到余弦变换，直至小波变换，这些数学模型都对图像处理技术的发展有着不可磨灭的贡献。本篇随笔主要介绍离散傅里叶变换（关于傅里叶变换原理的更加详尽的介绍请看《傅里叶变换与图像处理》）。
离散傅里叶变换的原理
对一张图像使用傅里叶变换就是将它分解成正弦和余弦两部分，也就是将图像从空间域（spatial domain）转换到频率域（frequency domain）。二维图像的傅里叶变换的数学公式：
其中的f是空间域值，F是频率域值。转换后频率域值是复数。显示傅里叶变换之后的结果需要使用实数图像（real image）加虚数图像（complex image），或者幅度图像（magitude image）加相位图像（phase image）的形式。在实际的图像处理过程中，仅仅使用了幅度图像，因为幅度图像包含了原图像的几乎所有处理所需的集合信息。在频域里面，对于一幅图像，高频部分代表了图像的细节、纹理信息；低频部分代表了图像的轮廓信息。如果对一幅精细图像使用低通滤波器，那么滤波后的结果就只剩下轮廓了。这与信号处理的基本思想是相通的。如果图像受到的噪声恰好位于某个特定的“频率”范围内，则可以通过滤波器来恢复原来的图像。傅里叶变换在图像处理中可以做到图像增强与图像去噪、图像分割之边缘检测、图像的特征提取、图像压缩等。
OpenCV傅里叶变换所用函数
dft()函数的作用是对一维或二维浮点数数组进行正向或反向离散傅里叶变换。关于这个函数的更详尽的介绍请看OpenCV的官方文档。
C++ : void dft(InputArray src, OutputArray dst, int flags = 0, int nonzeroRows = 0);
getOptimalDFTSize()函数返回给定向量尺寸的傅里叶最优尺寸大小。为了提高离散傅里叶变换的运行速度，需要扩充退选哪个，而具体扩充多少，就由这个函数计算得到。
C++ : int getOptimalDFTSize(int vecsize);
copyMakeBorder()函数的作用是扩充图像边界。
C++ : void copyMakeBorder(InputArray src, OutputArray dst,
int top, int bottom, int left, int right,
int borderType, const Scalar& value = Scalar() );
magnitude()函数用于计算二维矢量的幅值。
C++ : void magnitude(InputArray x, InputArray y, OutputArray magnitude);
log()函数用于计算每个数组元素绝对值的自然对数。
C++ : void log(InputArray src, OutputArray dst);
其原理：dst(I)={x|log|src(I)| if src(I)≠0, C otherwise}；
normalize()函数用于矩阵的归一化。
C++ : void normalize( InputArray src, InputOutputArray dst, double alpha = 1, double beta = 0,
int norm_type = NORM_L2, int dtype = -1, InputArray mask = noArray());
演示示例：
#include "opencv2/core/core.hpp" #include "opencv2/imgproc/imgproc.hpp" #include "opencv2/highgui/highgui.hpp" #include <iostream> using namespace cv; int main() { //【1】以灰度模式读取原始图像并显示 Mat srcImage = imread("1.png",0); if (!srcImage.data) { printf("读取图片错误，请确定目录下是否有imread函数指定图片存在~！ \n"); return false; } imshow("原始图像", srcImage); //【2】将输入图像延扩到最佳的尺寸，边界用0补充 int m = getOptimalDFTSize(srcImage.rows); int n = getOptimalDFTSize(srcImage.cols); //将添加的像素初始化为0. Mat padded; copyMakeBorder(srcImage, padded, 0, m - srcImage.rows, 0, n - srcImage.cols, BORDER_CONSTANT, Scalar::all(0)); //【3】为傅立叶变换的结果(实部和虚部)分配存储空间。 //将planes数组组合合并成一个多通道的数组complexI Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F) }; Mat complexI; merge(planes, 2, complexI); //【4】进行就地离散傅里叶变换 dft(complexI, complexI); //【5】将复数转换为幅值，即=> log(1 + sqrt(Re(DFT(I))^2 + Im(DFT(I))^2)) split(complexI, planes); // 将多通道数组complexI分离成几个单通道数组，planes[0] = Re(DFT(I), planes[1] = Im(DFT(I)) magnitude(planes[0], planes[1], planes[0]);// planes[0] = magnitude Mat magnitudeImage = planes[0]; //【6】进行对数尺度(logarithmic scale)缩放 magnitudeImage += Scalar::all(1); log(magnitudeImage, magnitudeImage);//求自然对数 //【8】归一化，用0到1之间的浮点值将矩阵变换为可视的图像格式 //此句代码的OpenCV2版为： //normalize(magnitudeImage, magnitudeImage, 0, 1, CV_MINMAX); //此句代码的OpenCV3版为: normalize(magnitudeImage, magnitudeImage, 0, 1, NORM_MINMAX); // 是这里的问题吗？ //【9】显示效果图 imshow("频谱幅值", magnitudeImage); //【7】剪切和重分布幅度图象限 //若有奇数行或奇数列，进行频谱裁剪 magnitudeImage = magnitudeImage(Rect(0, 0, magnitudeImage.cols & -2, magnitudeImage.rows & -2)); //重新排列傅立叶图像中的象限，使得原点位于图像中心 int cx = magnitudeImage.cols / 2; int cy = magnitudeImage.rows / 2; Mat q0(magnitudeImage, Rect(0, 0, cx, cy)); // ROI区域的左上 Mat q1(magnitudeImage, Rect(cx, 0, cx, cy)); // ROI区域的右上 Mat q2(magnitudeImage, Rect(0, cy, cx, cy)); // ROI区域的左下 Mat q3(magnitudeImage, Rect(cx, cy, cx, cy)); // ROI区域的右下 //交换象限（左上与右下进行交换） Mat tmp; q0.copyTo(tmp); q3.copyTo(q0); tmp.copyTo(q3); //交换象限（右上与左下进行交换） q1.copyTo(tmp); q2.copyTo(q1); tmp.copyTo(q2); //【9】显示效果图 imshow("原点频谱幅值", magnitudeImage); waitKey(); return 0; }
运行示例：
二维离散傅里叶变换的性质
离散傅里叶变换建立了函数在空间域到频率域之间的转换关系。这里简单地介绍一下二维离散傅里叶变换的基本性质：
1. 可分离性：一个二维离散傅里叶变换可以通过先后两次运用一维傅里叶变换来实现，即先沿f(x,y)的列方向求一维离散傅里叶变换得到F(x,v)，再对F(x,v)沿行的方向求一维离散傅里叶变换得到F(u,v)：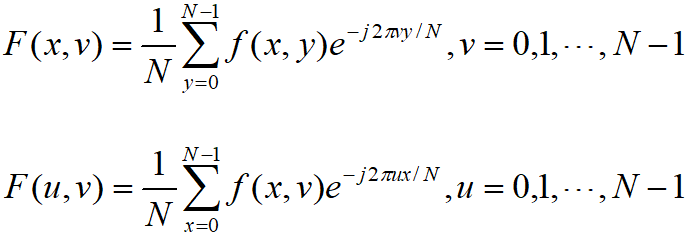
其中的过程如图示：
二维离散傅里叶反变换的分离过程和正变换的过程相似。
2. 平移性：傅里叶变换的平移性是指将f(x,y)乘以一个指数项相当于将其二维离散傅里叶变换F(u,v)的频域中心移动到新的位置。这个性质可以表示为：
从上式可知，对f(x,y)的平移不影响其傅里叶变换的幅值，只是在频域中发生了相移而已。反之，当频域中的F(u,v)产生相移时，相应的f(x,y)在空域中也只是发生了相移而幅值不变。那么如果要把图像的频谱原点从起始点(0,0)移到图像的中心点(N/2,N/2)，需要乘上一个什么因子呢？其简单的运算过程如下：
这个因子就是(-1)x+y。
3. 周期性：傅里叶正变换和反变换均以N为周期，即F(u,v)=F(u+N,v)=F(u,v+N)=F(u+N,v+N)。
4. 共轭对称性：如果f(x,y)是实函数，则它的傅里叶变换具有共轭对称性——F(u,v)=F*(-u,-v)，|F(u,v)|=|F(-u,-v)|。式中F*(u,v)是F(u,v)的复共轭。
5. 旋转不变形：对于旋转的描述，使用极坐标是非常方便的。所以这里引入极坐标使，
则f(x,y)和F(u,v)分别表示f(r,θ)和F(ω,φ)。容易得到公式，f(r,θ+θ0)↔F(ω,φ+θ0)。公式表明这样一个结论——如果f(x,y)在空域旋转θ0角度，则相应的傅里叶变换F(u,v)在频域上也旋转同一角度θ0。
6. 分配性和比例性：傅里叶变换的分配性表明它对于加法可以分配，而乘法则不行，如下式所示，
而傅里叶变换的比例性则表明对于两个标量a和b，有，
上式表明，在空间比例尺度的展宽，对应于在频域比例尺度的压缩，其幅值也减少为原来的1/|ab|。
实验一 实现二维傅里叶变换和逆变换
【实验目的】
通过实验，深入理解和掌握图像处理的基本技术，提高动手实践能力。
【实验环境】
MATLAB 和 VC++ 任选其一。（博主可能在某些地方使用 Python 进行实验）
【实验内容】
1）观察离散傅里叶频谱，并演示二维离散傅里叶变换的的主要性质（如平移性、旋转不变性、比例性、中心化）。
2）给出快速FFT变换与傅里叶变换的时间比较，并对图像进行反变换。
【实验步骤】
实验思路：原先博主想通过修改 OpenCV4 的 dft() 函数来演示傅里叶变换的主要性质的，但是博主在看了一下该函数的实现之后，觉得修改的代价比较大因此此篇博文不采用这种方法。下面请欣赏一下dft()函数的实现，由于 Intel 公司在该源文件的开头有相关的许可声明并且该函数的实现也调用了其他函数，所有本文将包含该函数的一个源文件给展示出来（注：安装了OpenCV的同学们，可以在***\opencv\sources\modules\core\src路径下，找到dxt.cpp。dft()函数的声明从3315行开始）。
1 /*M/////////////////////////////////////////////////////////////////////////////////////// 2 // 3 // IMPORTANT: READ BEFORE DOWNLOADING, COPYING, INSTALLING OR USING. 4 // 5 // By downloading, copying, installing or using the software you agree to this license. 6 // If you do not agree to this license, do not download, install, 7 // copy or use the software. 8 // 9 // 10 // Intel License Agreement 11 // For Open Source Computer Vision Library 12 // 13 // Copyright (C) 2000, Intel Corporation, all rights reserved. 14 // Third party copyrights are property of their respective owners. 15 // 16 // Redistribution and use in source and binary forms, with or without modification, 17 // are permitted provided that the following conditions are met: 18 // 19 // * Redistribution's of source code must retain the above copyright notice, 20 // this list of conditions and the following disclaimer. 21 // 22 // * Redistribution's in binary form must reproduce the above copyright notice, 23 // this list of conditions and the following disclaimer in the documentation 24 // and/or other materials provided with the distribution. 25 // 26 // * The name of Intel Corporation may not be used to endorse or promote products 27 // derived from this software without specific prior written permission. 28 // 29 // This software is provided by the copyright holders and contributors "as is" and 30 // any express or implied warranties, including, but not limited to, the implied 31 // warranties of merchantability and fitness for a particular purpose are disclaimed. 32 // In no event shall the Intel Corporation or contributors be liable for any direct, 33 // indirect, incidental, special, exemplary, or consequential damages 34 // (including, but not limited to, procurement of substitute goods or services; 35 // loss of use, data, or profits; or business interruption) however caused 36 // and on any theory of liability, whether in contract, strict liability, 37 // or tort (including negligence or otherwise) arising in any way out of 38 // the use of this software, even if advised of the possibility of such damage. 39 // 40 //M*/ 41 42 #include "precomp.hpp" 43 #include "opencv2/core/opencl/runtime/opencl_clamdfft.hpp" 44 #include "opencv2/core/opencl/runtime/opencl_core.hpp" 45 #include "opencl_kernels_core.hpp" 46 #include <map> 47 48 namespace cv 49 { 50 51 // On Win64 optimized versions of DFT and DCT fail the tests (fixed in VS2010) 52 #if defined _MSC_VER && !defined CV_ICC && defined _M_X64 && _MSC_VER < 1600 53 # pragma optimize("", off) 54 # pragma warning(disable: 4748) 55 #endif 56 57 #if IPP_VERSION_X100 >= 710 58 #define USE_IPP_DFT 1 59 #else 60 #undef USE_IPP_DFT 61 #endif 62 63 /****************************************************************************************\ 64 Discrete Fourier Transform 65 \****************************************************************************************/ 66 67 #define CV_MAX_LOCAL_DFT_SIZE (1 << 15) 68 69 static unsigned char bitrevTab[] = 70 { 71 0x00,0x80,0x40,0xc0,0x20,0xa0,0x60,0xe0,0x10,0x90,0x50,0xd0,0x30,0xb0,0x70,0xf0, 72 0x08,0x88,0x48,0xc8,0x28,0xa8,0x68,0xe8,0x18,0x98,0x58,0xd8,0x38,0xb8,0x78,0xf8, 73 0x04,0x84,0x44,0xc4,0x24,0xa4,0x64,0xe4,0x14,0x94,0x54,0xd4,0x34,0xb4,0x74,0xf4, 74 0x0c,0x8c,0x4c,0xcc,0x2c,0xac,0x6c,0xec,0x1c,0x9c,0x5c,0xdc,0x3c,0xbc,0x7c,0xfc, 75 0x02,0x82,0x42,0xc2,0x22,0xa2,0x62,0xe2,0x12,0x92,0x52,0xd2,0x32,0xb2,0x72,0xf2, 76 0x0a,0x8a,0x4a,0xca,0x2a,0xaa,0x6a,0xea,0x1a,0x9a,0x5a,0xda,0x3a,0xba,0x7a,0xfa, 77 0x06,0x86,0x46,0xc6,0x26,0xa6,0x66,0xe6,0x16,0x96,0x56,0xd6,0x36,0xb6,0x76,0xf6, 78 0x0e,0x8e,0x4e,0xce,0x2e,0xae,0x6e,0xee,0x1e,0x9e,0x5e,0xde,0x3e,0xbe,0x7e,0xfe, 79 0x01,0x81,0x41,0xc1,0x21,0xa1,0x61,0xe1,0x11,0x91,0x51,0xd1,0x31,0xb1,0x71,0xf1, 80 0x09,0x89,0x49,0xc9,0x29,0xa9,0x69,0xe9,0x19,0x99,0x59,0xd9,0x39,0xb9,0x79,0xf9, 81 0x05,0x85,0x45,0xc5,0x25,0xa5,0x65,0xe5,0x15,0x95,0x55,0xd5,0x35,0xb5,0x75,0xf5, 82 0x0d,0x8d,0x4d,0xcd,0x2d,0xad,0x6d,0xed,0x1d,0x9d,0x5d,0xdd,0x3d,0xbd,0x7d,0xfd, 83 0x03,0x83,0x43,0xc3,0x23,0xa3,0x63,0xe3,0x13,0x93,0x53,0xd3,0x33,0xb3,0x73,0xf3, 84 0x0b,0x8b,0x4b,0xcb,0x2b,0xab,0x6b,0xeb,0x1b,0x9b,0x5b,0xdb,0x3b,0xbb,0x7b,0xfb, 85 0x07,0x87,0x47,0xc7,0x27,0xa7,0x67,0xe7,0x17,0x97,0x57,0xd7,0x37,0xb7,0x77,0xf7, 86 0x0f,0x8f,0x4f,0xcf,0x2f,0xaf,0x6f,0xef,0x1f,0x9f,0x5f,0xdf,0x3f,0xbf,0x7f,0xff 87 }; 88 89 static const double DFTTab[][2] = 90 { 91 { 1.00000000000000000, 0.00000000000000000 }, 92 {-1.00000000000000000, 0.00000000000000000 }, 93 { 0.00000000000000000, 1.00000000000000000 }, 94 { 0.70710678118654757, 0.70710678118654746 }, 95 { 0.92387953251128674, 0.38268343236508978 }, 96 { 0.98078528040323043, 0.19509032201612825 }, 97 { 0.99518472667219693, 0.09801714032956060 }, 98 { 0.99879545620517241, 0.04906767432741802 }, 99 { 0.99969881869620425, 0.02454122852291229 }, 100 { 0.99992470183914450, 0.01227153828571993 }, 101 { 0.99998117528260111, 0.00613588464915448 }, 102 { 0.99999529380957619, 0.00306795676296598 }, 103 { 0.99999882345170188, 0.00153398018628477 }, 104 { 0.99999970586288223, 0.00076699031874270 }, 105 { 0.99999992646571789, 0.00038349518757140 }, 106 { 0.99999998161642933, 0.00019174759731070 }, 107 { 0.99999999540410733, 0.00009587379909598 }, 108 { 0.99999999885102686, 0.00004793689960307 }, 109 { 0.99999999971275666, 0.00002396844980842 }, 110 { 0.99999999992818922, 0.00001198422490507 }, 111 { 0.99999999998204725, 0.00000599211245264 }, 112 { 0.99999999999551181, 0.00000299605622633 }, 113 { 0.99999999999887801, 0.00000149802811317 }, 114 { 0.99999999999971945, 0.00000074901405658 }, 115 { 0.99999999999992983, 0.00000037450702829 }, 116 { 0.99999999999998246, 0.00000018725351415 }, 117 { 0.99999999999999567, 0.00000009362675707 }, 118 { 0.99999999999999889, 0.00000004681337854 }, 119 { 0.99999999999999978, 0.00000002340668927 }, 120 { 0.99999999999999989, 0.00000001170334463 }, 121 { 1.00000000000000000, 0.00000000585167232 }, 122 { 1.00000000000000000, 0.00000000292583616 } 123 }; 124 125 #define BitRev(i,shift) \ 126 ((int)((((unsigned)bitrevTab[(i)&255] << 24)+ \ 127 ((unsigned)bitrevTab[((i)>> 8)&255] << 16)+ \ 128 ((unsigned)bitrevTab[((i)>>16)&255] << 8)+ \ 129 ((unsigned)bitrevTab[((i)>>24)])) >> (shift))) 130 131 static int 132 DFTFactorize( int n, int* factors ) 133 { 134 int nf = 0, f, i, j; 135 136 if( n <= 5 ) 137 { 138 factors[0] = n; 139 return 1; 140 } 141 142 f = (((n - 1)^n)+1) >> 1; 143 if( f > 1 ) 144 { 145 factors[nf++] = f; 146 n = f == n ? 1 : n/f; 147 } 148 149 for( f = 3; n > 1; ) 150 { 151 int d = n/f; 152 if( d*f == n ) 153 { 154 factors[nf++] = f; 155 n = d; 156 } 157 else 158 { 159 f += 2; 160 if( f*f > n ) 161 break; 162 } 163 } 164 165 if( n > 1 ) 166 factors[nf++] = n; 167 168 f = (factors[0] & 1) == 0; 169 for( i = f; i < (nf+f)/2; i++ ) 170 CV_SWAP( factors[i], factors[nf-i-1+f], j ); 171 172 return nf; 173 } 174 175 static void 176 DFTInit( int n0, int nf, const int* factors, int* itab, int elem_size, void* _wave, int inv_itab ) 177 { 178 int digits[34], radix[34]; 179 int n = factors[0], m = 0; 180 int* itab0 = itab; 181 int i, j, k; 182 Complex<double> w, w1; 183 double t; 184 185 if( n0 <= 5 ) 186 { 187 itab[0] = 0; 188 itab[n0-1] = n0-1; 189 190 if( n0 != 4 ) 191 { 192 for( i = 1; i < n0-1; i++ ) 193 itab[i] = i; 194 } 195 else 196 { 197 itab[1] = 2; 198 itab[2] = 1; 199 } 200 if( n0 == 5 ) 201 { 202 if( elem_size == sizeof(Complex<double>) ) 203 ((Complex<double>*)_wave)[0] = Complex<double>(1.,0.); 204 else 205 ((Complex<float>*)_wave)[0] = Complex<float>(1.f,0.f); 206 } 207 if( n0 != 4 ) 208 return; 209 m = 2; 210 } 211 else 212 { 213 // radix[] is initialized from index 'nf' down to zero 214 assert (nf < 34); 215 radix[nf] = 1; 216 digits[nf] = 0; 217 for( i = 0; i < nf; i++ ) 218 { 219 digits[i] = 0; 220 radix[nf-i-1] = radix[nf-i]*factors[nf-i-1]; 221 } 222 223 if( inv_itab && factors[0] != factors[nf-1] ) 224 itab = (int*)_wave; 225 226 if( (n & 1) == 0 ) 227 { 228 int a = radix[1], na2 = n*a>>1, na4 = na2 >> 1; 229 for( m = 0; (unsigned)(1 << m) < (unsigned)n; m++ ) 230 ; 231 if( n <= 2 ) 232 { 233 itab[0] = 0; 234 itab[1] = na2; 235 } 236 else if( n <= 256 ) 237 { 238 int shift = 10 - m; 239 for( i = 0; i <= n - 4; i += 4 ) 240 { 241 j = (bitrevTab[i>>2]>>shift)*a; 242 itab[i] = j; 243 itab[i+1] = j + na2; 244 itab[i+2] = j + na4; 245 itab[i+3] = j + na2 + na4; 246 } 247 } 248 else 249 { 250 int shift = 34 - m; 251 for( i = 0; i < n; i += 4 ) 252 { 253 int i4 = i >> 2; 254 j = BitRev(i4,shift)*a; 255 itab[i] = j; 256 itab[i+1] = j + na2; 257 itab[i+2] = j + na4; 258 itab[i+3] = j + na2 + na4; 259 } 260 } 261 262 digits[1]++; 263 264 if( nf >= 2 ) 265 { 266 for( i = n, j = radix[2]; i < n0; ) 267 { 268 for( k = 0; k < n; k++ ) 269 itab[i+k] = itab[k] + j; 270 if( (i += n) >= n0 ) 271 break; 272 j += radix[2]; 273 for( k = 1; ++digits[k] >= factors[k]; k++ ) 274 { 275 digits[k] = 0; 276 j += radix[k+2] - radix[k]; 277 } 278 } 279 } 280 } 281 else 282 { 283 for( i = 0, j = 0;; ) 284 { 285 itab[i] = j; 286 if( ++i >= n0 ) 287 break; 288 j += radix[1]; 289 for( k = 0; ++digits[k] >= factors[k]; k++ ) 290 { 291 digits[k] = 0; 292 j += radix[k+2] - radix[k]; 293 } 294 } 295 } 296 297 if( itab != itab0 ) 298 { 299 itab0[0] = 0; 300 for( i = n0 & 1; i < n0; i += 2 ) 301 { 302 int k0 = itab[i]; 303 int k1 = itab[i+1]; 304 itab0[k0] = i; 305 itab0[k1] = i+1; 306 } 307 } 308 } 309 310 if( (n0 & (n0-1)) == 0 ) 311 { 312 w.re = w1.re = DFTTab[m][0]; 313 w.im = w1.im = -DFTTab[m][1]; 314 } 315 else 316 { 317 t = -CV_PI*2/n0; 318 w.im = w1.im = sin(t); 319 w.re = w1.re = std::sqrt(1. - w1.im*w1.im); 320 } 321 n = (n0+1)/2; 322 323 if( elem_size == sizeof(Complex<double>) ) 324 { 325 Complex<double>* wave = (Complex<double>*)_wave; 326 327 wave[0].re = 1.; 328 wave[0].im = 0.; 329 330 if( (n0 & 1) == 0 ) 331 { 332 wave[n].re = -1.; 333 wave[n].im = 0; 334 } 335 336 for( i = 1; i < n; i++ ) 337 { 338 wave[i] = w; 339 wave[n0-i].re = w.re; 340 wave[n0-i].im = -w.im; 341 342 t = w.re*w1.re - w.im*w1.im; 343 w.im = w.re*w1.im + w.im*w1.re; 344 w.re = t; 345 } 346 } 347 else 348 { 349 Complex<float>* wave = (Complex<float>*)_wave; 350 assert( elem_size == sizeof(Complex<float>) ); 351 352 wave[0].re = 1.f; 353 wave[0].im = 0.f; 354 355 if( (n0 & 1) == 0 ) 356 { 357 wave[n].re = -1.f; 358 wave[n].im = 0.f; 359 } 360 361 for( i = 1; i < n; i++ ) 362 { 363 wave[i].re = (float)w.re; 364 wave[i].im = (float)w.im; 365 wave[n0-i].re = (float)w.re; 366 wave[n0-i].im = (float)-w.im; 367 368 t = w.re*w1.re - w.im*w1.im; 369 w.im = w.re*w1.im + w.im*w1.re; 370 w.re = t; 371 } 372 } 373 } 374 375 template<typename T> struct DFT_VecR4 376 { 377 int operator()(Complex<T>*, int, int, int&, const Complex<T>*) const { return 1; } 378 }; 379 380 #if CV_SSE3 381 382 // optimized radix-4 transform 383 template<> struct DFT_VecR4<float> 384 { 385 int operator()(Complex<float>* dst, int N, int n0, int& _dw0, const Complex<float>* wave) const 386 { 387 int n = 1, i, j, nx, dw, dw0 = _dw0; 388 __m128 z = _mm_setzero_ps(), x02=z, x13=z, w01=z, w23=z, y01, y23, t0, t1; 389 Cv32suf t; t.i = 0x80000000; 390 __m128 neg0_mask = _mm_load_ss(&t.f); 391 __m128 neg3_mask = _mm_shuffle_ps(neg0_mask, neg0_mask, _MM_SHUFFLE(0,1,2,3)); 392 393 for( ; n*4 <= N; ) 394 { 395 nx = n; 396 n *= 4; 397 dw0 /= 4; 398 399 for( i = 0; i < n0; i += n ) 400 { 401 Complexf *v0, *v1; 402 403 v0 = dst + i; 404 v1 = v0 + nx*2; 405 406 x02 = _mm_loadl_pi(x02, (const __m64*)&v0[0]); 407 x13 = _mm_loadl_pi(x13, (const __m64*)&v0[nx]); 408 x02 = _mm_loadh_pi(x02, (const __m64*)&v1[0]); 409 x13 = _mm_loadh_pi(x13, (const __m64*)&v1[nx]); 410 411 y01 = _mm_add_ps(x02, x13); 412 y23 = _mm_sub_ps(x02, x13); 413 t1 = _mm_xor_ps(_mm_shuffle_ps(y01, y23, _MM_SHUFFLE(2,3,3,2)), neg3_mask); 414 t0 = _mm_movelh_ps(y01, y23); 415 y01 = _mm_add_ps(t0, t1); 416 y23 = _mm_sub_ps(t0, t1); 417 418 _mm_storel_pi((__m64*)&v0[0], y01); 419 _mm_storeh_pi((__m64*)&v0[nx], y01); 420 _mm_storel_pi((__m64*)&v1[0], y23); 421 _mm_storeh_pi((__m64*)&v1[nx], y23); 422 423 for( j = 1, dw = dw0; j < nx; j++, dw += dw0 ) 424 { 425 v0 = dst + i + j; 426 v1 = v0 + nx*2; 427 428 x13 = _mm_loadl_pi(x13, (const __m64*)&v0[nx]); 429 w23 = _mm_loadl_pi(w23, (const __m64*)&wave[dw*2]); 430 x13 = _mm_loadh_pi(x13, (const __m64*)&v1[nx]); // x1, x3 = r1 i1 r3 i3 431 w23 = _mm_loadh_pi(w23, (const __m64*)&wave[dw*3]); // w2, w3 = wr2 wi2 wr3 wi3 432 433 t0 = _mm_mul_ps(_mm_moveldup_ps(x13), w23); 434 t1 = _mm_mul_ps(_mm_movehdup_ps(x13), _mm_shuffle_ps(w23, w23, _MM_SHUFFLE(2,3,0,1))); 435 x13 = _mm_addsub_ps(t0, t1); 436 // re(x1*w2), im(x1*w2), re(x3*w3), im(x3*w3) 437 x02 = _mm_loadl_pi(x02, (const __m64*)&v1[0]); // x2 = r2 i2 438 w01 = _mm_loadl_pi(w01, (const __m64*)&wave[dw]); // w1 = wr1 wi1 439 x02 = _mm_shuffle_ps(x02, x02, _MM_SHUFFLE(0,0,1,1)); 440 w01 = _mm_shuffle_ps(w01, w01, _MM_SHUFFLE(1,0,0,1)); 441 x02 = _mm_mul_ps(x02, w01); 442 x02 = _mm_addsub_ps(x02, _mm_movelh_ps(x02, x02)); 443 // re(x0) im(x0) re(x2*w1), im(x2*w1) 444 x02 = _mm_loadl_pi(x02, (const __m64*)&v0[0]); 445 446 y01 = _mm_add_ps(x02, x13); 447 y23 = _mm_sub_ps(x02, x13); 448 t1 = _mm_xor_ps(_mm_shuffle_ps(y01, y23, _MM_SHUFFLE(2,3,3,2)), neg3_mask); 449 t0 = _mm_movelh_ps(y01, y23); 450 y01 = _mm_add_ps(t0, t1); 451 y23 = _mm_sub_ps(t0, t1); 452 453 _mm_storel_pi((__m64*)&v0[0], y01); 454 _mm_storeh_pi((__m64*)&v0[nx], y01); 455 _mm_storel_pi((__m64*)&v1[0], y23); 456 _mm_storeh_pi((__m64*)&v1[nx], y23); 457 } 458 } 459 } 460 461 _dw0 = dw0; 462 return n; 463 } 464 }; 465 466 #endif 467 468 #ifdef USE_IPP_DFT 469 static IppStatus ippsDFTFwd_CToC( const Complex<float>* src, Complex<float>* dst, 470 const void* spec, uchar* buf) 471 { 472 return CV_INSTRUMENT_FUN_IPP(ippsDFTFwd_CToC_32fc, (const Ipp32fc*)src, (Ipp32fc*)dst, 473 (const IppsDFTSpec_C_32fc*)spec, buf); 474 } 475 476 static IppStatus ippsDFTFwd_CToC( const Complex<double>* src, Complex<double>* dst, 477 const void* spec, uchar* buf) 478 { 479 return CV_INSTRUMENT_FUN_IPP(ippsDFTFwd_CToC_64fc, (const Ipp64fc*)src, (Ipp64fc*)dst, 480 (const IppsDFTSpec_C_64fc*)spec, buf); 481 } 482 483 static IppStatus ippsDFTInv_CToC( const Complex<float>* src, Complex<float>* dst, 484 const void* spec, uchar* buf) 485 { 486 return CV_INSTRUMENT_FUN_IPP(ippsDFTInv_CToC_32fc, (const Ipp32fc*)src, (Ipp32fc*)dst, 487 (const IppsDFTSpec_C_32fc*)spec, buf); 488 } 489 490 static IppStatus ippsDFTInv_CToC( const Complex<double>* src, Complex<double>* dst, 491 const void* spec, uchar* buf) 492 { 493 return CV_INSTRUMENT_FUN_IPP(ippsDFTInv_CToC_64fc, (const Ipp64fc*)src, (Ipp64fc*)dst, 494 (const IppsDFTSpec_C_64fc*)spec, buf); 495 } 496 497 static IppStatus ippsDFTFwd_RToPack( const float* src, float* dst, 498 const void* spec, uchar* buf) 499 { 500 return CV_INSTRUMENT_FUN_IPP(ippsDFTFwd_RToPack_32f, src, dst, (const IppsDFTSpec_R_32f*)spec, buf); 501 } 502 503 static IppStatus ippsDFTFwd_RToPack( const double* src, double* dst, 504 const void* spec, uchar* buf) 505 { 506 return CV_INSTRUMENT_FUN_IPP(ippsDFTFwd_RToPack_64f, src, dst, (const IppsDFTSpec_R_64f*)spec, buf); 507 } 508 509 static IppStatus ippsDFTInv_PackToR( const float* src, float* dst, 510 const void* spec, uchar* buf) 511 { 512 return CV_INSTRUMENT_FUN_IPP(ippsDFTInv_PackToR_32f, src, dst, (const IppsDFTSpec_R_32f*)spec, buf); 513 } 514 515 static IppStatus ippsDFTInv_PackToR( const double* src, double* dst, 516 const void* spec, uchar* buf) 517 { 518 return CV_INSTRUMENT_FUN_IPP(ippsDFTInv_PackToR_64f, src, dst, (const IppsDFTSpec_R_64f*)spec, buf); 519 } 520 #endif 521 522 struct OcvDftOptions; 523 524 typedef void (*DFTFunc)(const OcvDftOptions & c, const void* src, void* dst); 525 526 struct OcvDftOptions { 527 int nf; 528 int *factors; 529 double scale; 530 531 int* itab; 532 void* wave; 533 int tab_size; 534 int n; 535 536 bool isInverse; 537 bool noPermute; 538 bool isComplex; 539 540 bool haveSSE3; 541 542 DFTFunc dft_func; 543 bool useIpp; 544 545 #ifdef USE_IPP_DFT 546 uchar* ipp_spec; 547 uchar* ipp_work; 548 #endif 549 550 OcvDftOptions() 551 { 552 nf = 0; 553 factors = 0; 554 scale = 0; 555 itab = 0; 556 wave = 0; 557 tab_size = 0; 558 n = 0; 559 isInverse = false; 560 noPermute = false; 561 isComplex = false; 562 useIpp = false; 563 #ifdef USE_IPP_DFT 564 ipp_spec = 0; 565 ipp_work = 0; 566 #endif 567 dft_func = 0; 568 haveSSE3 = checkHardwareSupport(CV_CPU_SSE3); 569 } 570 }; 571 572 // mixed-radix complex discrete Fourier transform: double-precision version 573 template<typename T> static void 574 DFT(const OcvDftOptions & c, const Complex<T>* src, Complex<T>* dst) 575 { 576 static const T sin_120 = (T)0.86602540378443864676372317075294; 577 static const T fft5_2 = (T)0.559016994374947424102293417182819; 578 static const T fft5_3 = (T)-0.951056516295153572116439333379382; 579 static const T fft5_4 = (T)-1.538841768587626701285145288018455; 580 static const T fft5_5 = (T)0.363271264002680442947733378740309; 581 582 const Complex<T>* wave = (Complex<T>*)c.wave; 583 const int * itab = c.itab; 584 585 int n = c.n; 586 int f_idx, nx; 587 int inv = c.isInverse; 588 int dw0 = c.tab_size, dw; 589 int i, j, k; 590 Complex<T> t; 591 T scale = (T)c.scale; 592 593 if( c.useIpp ) 594 { 595 #ifdef USE_IPP_DFT 596 if( !inv ) 597 { 598 if (ippsDFTFwd_CToC( src, dst, c.ipp_spec, c.ipp_work ) >= 0) 599 { 600 CV_IMPL_ADD(CV_IMPL_IPP); 601 return; 602 } 603 } 604 else 605 { 606 if (ippsDFTInv_CToC( src, dst, c.ipp_spec, c.ipp_work ) >= 0) 607 { 608 CV_IMPL_ADD(CV_IMPL_IPP); 609 return; 610 } 611 } 612 setIppErrorStatus(); 613 #endif 614 } 615 616 int tab_step = c.tab_size == n ? 1 : c.tab_size == n*2 ? 2 : c.tab_size/n; 617 618 // 0. shuffle data 619 if( dst != src ) 620 { 621 assert( !c.noPermute ); 622 if( !inv ) 623 { 624 for( i = 0; i <= n - 2; i += 2, itab += 2*tab_step ) 625 { 626 int k0 = itab[0], k1 = itab[tab_step]; 627 assert( (unsigned)k0 < (unsigned)n && (unsigned)k1 < (unsigned)n ); 628 dst[i] = src[k0]; dst[i+1] = src[k1]; 629 } 630 631 if( i < n ) 632 dst[n-1] = src[n-1]; 633 } 634 else 635 { 636 for( i = 0; i <= n - 2; i += 2, itab += 2*tab_step ) 637 { 638 int k0 = itab[0], k1 = itab[tab_step]; 639 assert( (unsigned)k0 < (unsigned)n && (unsigned)k1 < (unsigned)n ); 640 t.re = src[k0].re; t.im = -src[k0].im; 641 dst[i] = t; 642 t.re = src[k1].re; t.im = -src[k1].im; 643 dst[i+1] = t; 644 } 645 646 if( i < n ) 647 { 648 t.re = src[n-1].re; t.im = -src[n-1].im; 649 dst[i] = t; 650 } 651 } 652 } 653 else 654 { 655 if( !c.noPermute ) 656 { 657 CV_Assert( c.factors[0] == c.factors[c.nf-1] ); 658 if( c.nf == 1 ) 659 { 660 if( (n & 3) == 0 ) 661 { 662 int n2 = n/2; 663 Complex<T>* dsth = dst + n2; 664 665 for( i = 0; i < n2; i += 2, itab += tab_step*2 ) 666 { 667 j = itab[0]; 668 assert( (unsigned)j < (unsigned)n2 ); 669 670 CV_SWAP(dst[i+1], dsth[j], t); 671 if( j > i ) 672 { 673 CV_SWAP(dst[i], dst[j], t); 674 CV_SWAP(dsth[i+1], dsth[j+1], t); 675 } 676 } 677 } 678 // else do nothing 679 } 680 else 681 { 682 for( i = 0; i < n; i++, itab += tab_step ) 683 { 684 j = itab[0]; 685 assert( (unsigned)j < (unsigned)n ); 686 if( j > i ) 687 CV_SWAP(dst[i], dst[j], t); 688 } 689 } 690 } 691 692 if( inv ) 693 { 694 for( i = 0; i <= n - 2; i += 2 ) 695 { 696 T t0 = -dst[i].im; 697 T t1 = -dst[i+1].im; 698 dst[i].im = t0; dst[i+1].im = t1; 699 } 700 701 if( i < n ) 702 dst[n-1].im = -dst[n-1].im; 703 } 704 } 705 706 n = 1; 707 // 1. power-2 transforms 708 if( (c.factors[0] & 1) == 0 ) 709 { 710 if( c.factors[0] >= 4 && c.haveSSE3) 711 { 712 DFT_VecR4<T> vr4; 713 n = vr4(dst, c.factors[0], c.n, dw0, wave); 714 } 715 716 // radix-4 transform 717 for( ; n*4 <= c.factors[0]; ) 718 { 719 nx = n; 720 n *= 4; 721 dw0 /= 4; 722 723 for( i = 0; i < c.n; i += n ) 724 { 725 Complex<T> *v0, *v1; 726 T r0, i0, r1, i1, r2, i2, r3, i3, r4, i4; 727 728 v0 = dst + i; 729 v1 = v0 + nx*2; 730 731 r0 = v1[0].re; i0 = v1[0].im; 732 r4 = v1[nx].re; i4 = v1[nx].im; 733 734 r1 = r0 + r4; i1 = i0 + i4; 735 r3 = i0 - i4; i3 = r4 - r0; 736 737 r2 = v0[0].re; i2 = v0[0].im; 738 r4 = v0[nx].re; i4 = v0[nx].im; 739 740 r0 = r2 + r4; i0 = i2 + i4; 741 r2 -= r4; i2 -= i4; 742 743 v0[0].re = r0 + r1; v0[0].im = i0 + i1; 744 v1[0].re = r0 - r1; v1[0].im = i0 - i1; 745 v0[nx].re = r2 + r3; v0[nx].im = i2 + i3; 746 v1[nx].re = r2 - r3; v1[nx].im = i2 - i3; 747 748 for( j = 1, dw = dw0; j < nx; j++, dw += dw0 ) 749 { 750 v0 = dst + i + j; 751 v1 = v0 + nx*2; 752 753 r2 = v0[nx].re*wave[dw*2].re - v0[nx].im*wave[dw*2].im; 754 i2 = v0[nx].re*wave[dw*2].im + v0[nx].im*wave[dw*2].re; 755 r0 = v1[0].re*wave[dw].im + v1[0].im*wave[dw].re; 756 i0 = v1[0].re*wave[dw].re - v1[0].im*wave[dw].im; 757 r3 = v1[nx].re*wave[dw*3].im + v1[nx].im*wave[dw*3].re; 758 i3 = v1[nx].re*wave[dw*3].re - v1[nx].im*wave[dw*3].im; 759 760 r1 = i0 + i3; i1 = r0 + r3; 761 r3 = r0 - r3; i3 = i3 - i0; 762 r4 = v0[0].re; i4 = v0[0].im; 763 764 r0 = r4 + r2; i0 = i4 + i2; 765 r2 = r4 - r2; i2 = i4 - i2; 766 767 v0[0].re = r0 + r1; v0[0].im = i0 + i1; 768 v1[0].re = r0 - r1; v1[0].im = i0 - i1; 769 v0[nx].re = r2 + r3; v0[nx].im = i2 + i3; 770 v1[nx].re = r2 - r3; v1[nx].im = i2 - i3; 771 } 772 } 773 } 774 775 for( ; n < c.factors[0]; ) 776 { 777 // do the remaining radix-2 transform 778 nx = n; 779 n *= 2; 780 dw0 /= 2; 781 782 for( i = 0; i < c.n; i += n ) 783 { 784 Complex<T>* v = dst + i; 785 T r0 = v[0].re + v[nx].re; 786 T i0 = v[0].im + v[nx].im; 787 T r1 = v[0].re - v[nx].re; 788 T i1 = v[0].im - v[nx].im; 789 v[0].re = r0; v[0].im = i0; 790 v[nx].re = r1; v[nx].im = i1; 791 792 for( j = 1, dw = dw0; j < nx; j++, dw += dw0 ) 793 { 794 v = dst + i + j; 795 r1 = v[nx].re*wave[dw].re - v[nx].im*wave[dw].im; 796 i1 = v[nx].im*wave[dw].re + v[nx].re*wave[dw].im; 797 r0 = v[0].re; i0 = v[0].im; 798 799 v[0].re = r0 + r1; v[0].im = i0 + i1; 800 v[nx].re = r0 - r1; v[nx].im = i0 - i1; 801 } 802 } 803 } 804 } 805 806 // 2. all the other transforms 807 for( f_idx = (c.factors[0]&1) ? 0 : 1; f_idx < c.nf; f_idx++ ) 808 { 809 int factor = c.factors[f_idx]; 810 nx = n; 811 n *= factor; 812 dw0 /= factor; 813 814 if( factor == 3 ) 815 { 816 // radix-3 817 for( i = 0; i < c.n; i += n ) 818 { 819 Complex<T>* v = dst + i; 820 821 T r1 = v[nx].re + v[nx*2].re; 822 T i1 = v[nx].im + v[nx*2].im; 823 T r0 = v[0].re; 824 T i0 = v[0].im; 825 T r2 = sin_120*(v[nx].im - v[nx*2].im); 826 T i2 = sin_120*(v[nx*2].re - v[nx].re); 827 v[0].re = r0 + r1; v[0].im = i0 + i1; 828 r0 -= (T)0.5*r1; i0 -= (T)0.5*i1; 829 v[nx].re = r0 + r2; v[nx].im = i0 + i2; 830 v[nx*2].re = r0 - r2; v[nx*2].im = i0 - i2; 831 832 for( j = 1, dw = dw0; j < nx; j++, dw += dw0 ) 833 { 834 v = dst + i + j; 835 r0 = v[nx].re*wave[dw].re - v[nx].im*wave[dw].im; 836 i0 = v[nx].re*wave[dw].im + v[nx].im*wave[dw].re; 837 i2 = v[nx*2].re*wave[dw*2].re - v[nx*2].im*wave[dw*2].im; 838 r2 = v[nx*2].re*wave[dw*2].im + v[nx*2].im*wave[dw*2].re; 839 r1 = r0 + i2; i1 = i0 + r2; 840 841 r2 = sin_120*(i0 - r2); i2 = sin_120*(i2 - r0); 842 r0 = v[0].re; i0 = v[0].im; 843 v[0].re = r0 + r1; v[0].im = i0 + i1; 844 r0 -= (T)0.5*r1; i0 -= (T)0.5*i1; 845 v[nx].re = r0 + r2; v[nx].im = i0 + i2; 846 v[nx*2].re = r0 - r2; v[nx*2].im = i0 - i2; 847 } 848 } 849 } 850 else if( factor == 5 ) 851 { 852 // radix-5 853 for( i = 0; i < c.n; i += n ) 854 { 855 for( j = 0, dw = 0; j < nx; j++, dw += dw0 ) 856 { 857 Complex<T>* v0 = dst + i + j; 858 Complex<T>* v1 = v0 + nx*2; 859 Complex<T>* v2 = v1 + nx*2; 860 861 T r0, i0, r1, i1, r2, i2, r3, i3, r4, i4, r5, i5; 862 863 r3 = v0[nx].re*wave[dw].re - v0[nx].im*wave[dw].im; 864 i3 = v0[nx].re*wave[dw].im + v0[nx].im*wave[dw].re; 865 r2 = v2[0].re*wave[dw*4].re - v2[0].im*wave[dw*4].im; 866 i2 = v2[0].re*wave[dw*4].im + v2[0].im*wave[dw*4].re; 867 868 r1 = r3 + r2; i1 = i3 + i2; 869 r3 -= r2; i3 -= i2; 870 871 r4 = v1[nx].re*wave[dw*3].re - v1[nx].im*wave[dw*3].im; 872 i4 = v1[nx].re*wave[dw*3].im + v1[nx].im*wave[dw*3].re; 873 r0 = v1[0].re*wave[dw*2].re - v1[0].im*wave[dw*2].im; 874 i0 = v1[0].re*wave[dw*2].im + v1[0].im*wave[dw*2].re; 875 876 r2 = r4 + r0; i2 = i4 + i0; 877 r4 -= r0; i4 -= i0; 878 879 r0 = v0[0].re; i0 = v0[0].im; 880 r5 = r1 + r2; i5 = i1 + i2; 881 882 v0[0].re = r0 + r5; v0[0].im = i0 + i5; 883 884 r0 -= (T)0.25*r5; i0 -= (T)0.25*i5; 885 r1 = fft5_2*(r1 - r2); i1 = fft5_2*(i1 - i2); 886 r2 = -fft5_3*(i3 + i4); i2 = fft5_3*(r3 + r4); 887 888 i3 *= -fft5_5; r3 *= fft5_5; 889 i4 *= -fft5_4; r4 *= fft5_4; 890 891 r5 = r2 + i3; i5 = i2 + r3; 892 r2 -= i4; i2 -= r4; 893 894 r3 = r0 + r1; i3 = i0 + i1; 895 r0 -= r1; i0 -= i1; 896 897 v0[nx].re = r3 + r2; v0[nx].im = i3 + i2; 898 v2[0].re = r3 - r2; v2[0].im = i3 - i2; 899 900 v1[0].re = r0 + r5; v1[0].im = i0 + i5; 901 v1[nx].re = r0 - r5; v1[nx].im = i0 - i5; 902 } 903 } 904 } 905 else 906 { 907 // radix-"factor" - an odd number 908 int p, q, factor2 = (factor - 1)/2; 909 int d, dd, dw_f = c.tab_size/factor; 910 AutoBuffer<Complex<T> > buf(factor2 * 2); 911 Complex<T>* a = buf.data(); 912 Complex<T>* b = a + factor2; 913 914 for( i = 0; i < c.n; i += n ) 915 { 916 for( j = 0, dw = 0; j < nx; j++, dw += dw0 ) 917 { 918 Complex<T>* v = dst + i + j; 919 Complex<T> v_0 = v[0]; 920 Complex<T> vn_0 = v_0; 921 922 if( j == 0 ) 923 { 924 for( p = 1, k = nx; p <= factor2; p++, k += nx ) 925 { 926 T r0 = v[k].re + v[n-k].re; 927 T i0 = v[k].im - v[n-k].im; 928 T r1 = v[k].re - v[n-k].re; 929 T i1 = v[k].im + v[n-k].im; 930 931 vn_0.re += r0; vn_0.im += i1; 932 a[p-1].re = r0; a[p-1].im = i0; 933 b[p-1].re = r1; b[p-1].im = i1; 934 } 935 } 936 else 937 { 938 const Complex<T>* wave_ = wave + dw*factor; 939 d = dw; 940 941 for( p = 1, k = nx; p <= factor2; p++, k += nx, d += dw ) 942 { 943 T r2 = v[k].re*wave[d].re - v[k].im*wave[d].im; 944 T i2 = v[k].re*wave[d].im + v[k].im*wave[d].re; 945 946 T r1 = v[n-k].re*wave_[-d].re - v[n-k].im*wave_[-d].im; 947 T i1 = v[n-k].re*wave_[-d].im + v[n-k].im*wave_[-d].re; 948 949 T r0 = r2 + r1; 950 T i0 = i2 - i1; 951 r1 = r2 - r1; 952 i1 = i2 + i1; 953 954 vn_0.re += r0; vn_0.im += i1; 955 a[p-1].re = r0; a[p-1].im = i0; 956 b[p-1].re = r1; b[p-1].im = i1; 957 } 958 } 959 960 v[0] = vn_0; 961 962 for( p = 1, k = nx; p <= factor2; p++, k += nx ) 963 { 964 Complex<T> s0 = v_0, s1 = v_0; 965 d = dd = dw_f*p; 966 967 for( q = 0; q < factor2; q++ ) 968 { 969 T r0 = wave[d].re * a[q].re; 970 T i0 = wave[d].im * a[q].im; 971 T r1 = wave[d].re * b[q].im; 972 T i1 = wave[d].im * b[q].re; 973 974 s1.re += r0 + i0; s0.re += r0 - i0; 975 s1.im += r1 - i1; s0.im += r1 + i1; 976 977 d += dd; 978 d -= -(d >= c.tab_size) & c.tab_size; 979 } 980 981 v[k] = s0; 982 v[n-k] = s1; 983 } 984 } 985 } 986 } 987 } 988 989 if( scale != 1 ) 990 { 991 T re_scale = scale, im_scale = scale; 992 if( inv ) 993 im_scale = -im_scale; 994 995 for( i = 0; i < c.n; i++ ) 996 { 997 T t0 = dst[i].re*re_scale; 998 T t1 = dst[i].im*im_scale; 999 dst[i].re = t0; 1000 dst[i].im = t1; 1001 } 1002 } 1003 else if( inv ) 1004 { 1005 for( i = 0; i <= c.n - 2; i += 2 ) 1006 { 1007 T t0 = -dst[i].im; 1008 T t1 = -dst[i+1].im; 1009 dst[i].im = t0; 1010 dst[i+1].im = t1; 1011 } 1012 1013 if( i < c.n ) 1014 dst[c.n-1].im = -dst[c.n-1].im; 1015 } 1016 } 1017 1018 1019 /* FFT of real vector 1020 output vector format: 1021 re(0), re(1), im(1), ... , re(n/2-1), im((n+1)/2-1) [, re((n+1)/2)] OR ... 1022 re(0), 0, re(1), im(1), ..., re(n/2-1), im((n+1)/2-1) [, re((n+1)/2), 0] */ 1023 template<typename T> static void 1024 RealDFT(const OcvDftOptions & c, const T* src, T* dst) 1025 { 1026 int n = c.n; 1027 int complex_output = c.isComplex; 1028 T scale = (T)c.scale; 1029 int j; 1030 dst += complex_output; 1031 1032 if( c.useIpp ) 1033 { 1034 #ifdef USE_IPP_DFT 1035 if (ippsDFTFwd_RToPack( src, dst, c.ipp_spec, c.ipp_work ) >=0) 1036 { 1037 if( complex_output ) 1038 { 1039 dst[-1] = dst[0]; 1040 dst[0] = 0; 1041 if( (n & 1) == 0 ) 1042 dst[n] = 0; 1043 } 1044 CV_IMPL_ADD(CV_IMPL_IPP); 1045 return; 1046 } 1047 setIppErrorStatus(); 1048 #endif 1049 } 1050 assert( c.tab_size == n ); 1051 1052 if( n == 1 ) 1053 { 1054 dst[0] = src[0]*scale; 1055 } 1056 else if( n == 2 ) 1057 { 1058 T t = (src[0] + src[1])*scale; 1059 dst[1] = (src[0] - src[1])*scale; 1060 dst[0] = t; 1061 } 1062 else if( n & 1 ) 1063 { 1064 dst -= complex_output; 1065 Complex<T>* _dst = (Complex<T>*)dst; 1066 _dst[0].re = src[0]*scale; 1067 _dst[0].im = 0; 1068 for( j = 1; j < n; j += 2 ) 1069 { 1070 T t0 = src[c.itab[j]]*scale; 1071 T t1 = src[c.itab[j+1]]*scale; 1072 _dst[j].re = t0; 1073 _dst[j].im = 0; 1074 _dst[j+1].re = t1; 1075 _dst[j+1].im = 0; 1076 } 1077 OcvDftOptions sub_c = c; 1078 sub_c.isComplex = false; 1079 sub_c.isInverse = false; 1080 sub_c.noPermute = true; 1081 sub_c.scale = 1.; 1082 DFT(sub_c, _dst, _dst); 1083 if( !complex_output ) 1084 dst[1] = dst[0]; 1085 } 1086 else 1087 { 1088 T t0, t; 1089 T h1_re, h1_im, h2_re, h2_im; 1090 T scale2 = scale*(T)0.5; 1091 int n2 = n >> 1; 1092 1093 c.factors[0] >>= 1; 1094 1095 OcvDftOptions sub_c = c; 1096 sub_c.factors += (c.factors[0] == 1); 1097 sub_c.nf -= (c.factors[0] == 1); 1098 sub_c.isComplex = false; 1099 sub_c.isInverse = false; 1100 sub_c.noPermute = false; 1101 sub_c.scale = 1.; 1102 sub_c.n = n2; 1103 1104 DFT(sub_c, (Complex<T>*)src, (Complex<T>*)dst); 1105 1106 c.factors[0] <<= 1; 1107 1108 t = dst[0] - dst[1]; 1109 dst[0] = (dst[0] + dst[1])*scale; 1110 dst[1] = t*scale; 1111 1112 t0 = dst[n2]; 1113 t = dst[n-1]; 1114 dst[n-1] = dst[1]; 1115 1116 const Complex<T> *wave = (const Complex<T>*)c.wave; 1117 1118 for( j = 2, wave++; j < n2; j += 2, wave++ ) 1119 { 1120 /* calc odd */ 1121 h2_re = scale2*(dst[j+1] + t); 1122 h2_im = scale2*(dst[n-j] - dst[j]); 1123 1124 /* calc even */ 1125 h1_re = scale2*(dst[j] + dst[n-j]); 1126 h1_im = scale2*(dst[j+1] - t); 1127 1128 /* rotate */ 1129 t = h2_re*wave->re - h2_im*wave->im; 1130 h2_im = h2_re*wave->im + h2_im*wave->re; 1131 h2_re = t; 1132 t = dst[n-j-1]; 1133 1134 dst[j-1] = h1_re + h2_re; 1135 dst[n-j-1] = h1_re - h2_re; 1136 dst[j] = h1_im + h2_im; 1137 dst[n-j] = h2_im - h1_im; 1138 } 1139 1140 if( j <= n2 ) 1141 { 1142 dst[n2-1] = t0*scale; 1143 dst[n2] = -t*scale; 1144 } 1145 } 1146 1147 if( complex_output && ((n & 1) == 0 || n == 1)) 1148 { 1149 dst[-1] = dst[0]; 1150 dst[0] = 0; 1151 if( n > 1 ) 1152 dst[n] = 0; 1153 } 1154 } 1155 1156 /* Inverse FFT of complex conjugate-symmetric vector 1157 input vector format: 1158 re[0], re[1], im[1], ... , re[n/2-1], im[n/2-1], re[n/2] OR 1159 re(0), 0, re(1), im(1), ..., re(n/2-1), im((n+1)/2-1) [, re((n+1)/2), 0] */ 1160 template<typename T> static void 1161 CCSIDFT(const OcvDftOptions & c, const T* src, T* dst) 1162 { 1163 int n = c.n; 1164 int complex_input = c.isComplex; 1165 int j, k; 1166 T scale = (T)c.scale; 1167 T save_s1 = 0.; 1168 T t0, t1, t2, t3, t; 1169 1170 assert( c.tab_size == n ); 1171 1172 if( complex_input ) 1173 { 1174 assert( src != dst ); 1175 save_s1 = src[1]; 1176 ((T*)src)[1] = src[0]; 1177 src++; 1178 } 1179 if( c.useIpp ) 1180 { 1181 #ifdef USE_IPP_DFT 1182 if (ippsDFTInv_PackToR( src, dst, c.ipp_spec, c.ipp_work ) >=0) 1183 { 1184 if( complex_input ) 1185 ((T*)src)[0] = (T)save_s1; 1186 CV_IMPL_ADD(CV_IMPL_IPP); 1187 return; 1188 } 1189 1190 setIppErrorStatus(); 1191 #endif 1192 } 1193 if( n == 1 ) 1194 { 1195 dst[0] = (T)(src[0]*scale); 1196 } 1197 else if( n == 2 ) 1198 { 1199 t = (src[0] + src[1])*scale; 1200 dst[1] = (src[0] - src[1])*scale; 1201 dst[0] = t; 1202 } 1203 else if( n & 1 ) 1204 { 1205 Complex<T>* _src = (Complex<T>*)(src-1); 1206 Complex<T>* _dst = (Complex<T>*)dst; 1207 1208 _dst[0].re = src[0]; 1209 _dst[0].im = 0; 1210 1211 int n2 = (n+1) >> 1; 1212 1213 for( j = 1; j < n2; j++ ) 1214 { 1215 int k0 = c.itab[j], k1 = c.itab[n-j]; 1216 t0 = _src[j].re; t1 = _src[j].im; 1217 _dst[k0].re = t0; _dst[k0].im = -t1; 1218 _dst[k1].re = t0; _dst[k1].im = t1; 1219 } 1220 1221 OcvDftOptions sub_c = c; 1222 sub_c.isComplex = false; 1223 sub_c.isInverse = false; 1224 sub_c.noPermute = true; 1225 sub_c.scale = 1.; 1226 sub_c.n = n; 1227 1228 DFT(sub_c, _dst, _dst); 1229 dst[0] *= scale; 1230 for( j = 1; j < n; j += 2 ) 1231 { 1232 t0 = dst[j*2]*scale; 1233 t1 = dst[j*2+2]*scale; 1234 dst[j] = t0; 1235 dst[j+1] = t1; 1236 } 1237 } 1238 else 1239 { 1240 int inplace = src == dst; 1241 const Complex<T>* w = (const Complex<T>*)c.wave; 1242 1243 t = src[1]; 1244 t0 = (src[0] + src[n-1]); 1245 t1 = (src[n-1] - src[0]); 1246 dst[0] = t0; 1247 dst[1] = t1; 1248 1249 int n2 = (n+1) >> 1; 1250 1251 for( j = 2, w++; j < n2; j += 2, w++ ) 1252 { 1253 T h1_re, h1_im, h2_re, h2_im; 1254 1255 h1_re = (t + src[n-j-1]); 1256 h1_im = (src[j] - src[n-j]); 1257 1258 h2_re = (t - src[n-j-1]); 1259 h2_im = (src[j] + src[n-j]); 1260 1261 t = h2_re*w->re + h2_im*w->im; 1262 h2_im = h2_im*w->re - h2_re*w->im; 1263 h2_re = t; 1264 1265 t = src[j+1]; 1266 t0 = h1_re - h2_im; 1267 t1 = -h1_im - h2_re; 1268 t2 = h1_re + h2_im; 1269 t3 = h1_im - h2_re; 1270 1271 if( inplace ) 1272 { 1273 dst[j] = t0; 1274 dst[j+1] = t1; 1275 dst[n-j] = t2; 1276 dst[n-j+1]= t3; 1277 } 1278 else 1279 { 1280 int j2 = j >> 1; 1281 k = c.itab[j2]; 1282 dst[k] = t0; 1283 dst[k+1] = t1; 1284 k = c.itab[n2-j2]; 1285 dst[k] = t2; 1286 dst[k+1]= t3; 1287 } 1288 } 1289 1290 if( j <= n2 ) 1291 { 1292 t0 = t*2; 1293 t1 = src[n2]*2; 1294 1295 if( inplace ) 1296 { 1297 dst[n2] = t0; 1298 dst[n2+1] = t1; 1299 } 1300 else 1301 { 1302 k = c.itab[n2]; 1303 dst[k*2] = t0; 1304 dst[k*2+1] = t1; 1305 } 1306 } 1307 1308 c.factors[0] >>= 1; 1309 1310 OcvDftOptions sub_c = c; 1311 sub_c.factors += (c.factors[0] == 1); 1312 sub_c.nf -= (c.factors[0] == 1); 1313 sub_c.isComplex = false; 1314 sub_c.isInverse = false; 1315 sub_c.noPermute = !inplace; 1316 sub_c.scale = 1.; 1317 sub_c.n = n2; 1318 1319 DFT(sub_c, (Complex<T>*)dst, (Complex<T>*)dst); 1320 1321 c.factors[0] <<= 1; 1322 1323 for( j = 0; j < n; j += 2 ) 1324 { 1325 t0 = dst[j]*scale; 1326 t1 = dst[j+1]*(-scale); 1327 dst[j] = t0; 1328 dst[j+1] = t1; 1329 } 1330 } 1331 if( complex_input ) 1332 ((T*)src)[0] = (T)save_s1; 1333 } 1334 1335 static void 1336 CopyColumn( const uchar* _src, size_t src_step, 1337 uchar* _dst, size_t dst_step, 1338 int len, size_t elem_size ) 1339 { 1340 int i, t0, t1; 1341 const int* src = (const int*)_src; 1342 int* dst = (int*)_dst; 1343 src_step /= sizeof(src[0]); 1344 dst_step /= sizeof(dst[0]); 1345 1346 if( elem_size == sizeof(int) ) 1347 { 1348 for( i = 0; i < len; i++, src += src_step, dst += dst_step ) 1349 dst[0] = src[0]; 1350 } 1351 else if( elem_size == sizeof(int)*2 ) 1352 { 1353 for( i = 0; i < len; i++, src += src_step, dst += dst_step ) 1354 { 1355 t0 = src[0]; t1 = src[1]; 1356 dst[0] = t0; dst[1] = t1; 1357 } 1358 } 1359 else if( elem_size == sizeof(int)*4 ) 1360 { 1361 for( i = 0; i < len; i++, src += src_step, dst += dst_step ) 1362 { 1363 t0 = src[0]; t1 = src[1]; 1364 dst[0] = t0; dst[1] = t1; 1365 t0 = src[2]; t1 = src[3]; 1366 dst[2] = t0; dst[3] = t1; 1367 } 1368 } 1369 } 1370 1371 1372 static void 1373 CopyFrom2Columns( const uchar* _src, size_t src_step, 1374 uchar* _dst0, uchar* _dst1, 1375 int len, size_t elem_size ) 1376 { 1377 int i, t0, t1; 1378 const int* src = (const int*)_src; 1379 int* dst0 = (int*)_dst0; 1380 int* dst1 = (int*)_dst1; 1381 src_step /= sizeof(src[0]); 1382 1383 if( elem_size == sizeof(int) ) 1384 { 1385 for( i = 0; i < len; i++, src += src_step ) 1386 { 1387 t0 = src[0]; t1 = src[1]; 1388 dst0[i] = t0; dst1[i] = t1; 1389 } 1390 } 1391 else if( elem_size == sizeof(int)*2 ) 1392 { 1393 for( i = 0; i < len*2; i += 2, src += src_step ) 1394 { 1395 t0 = src[0]; t1 = src[1]; 1396 dst0[i] = t0; dst0[i+1] = t1; 1397 t0 = src[2]; t1 = src[3]; 1398 dst1[i] = t0; dst1[i+1] = t1; 1399 } 1400 } 1401 else if( elem_size == sizeof(int)*4 ) 1402 { 1403 for( i = 0; i < len*4; i += 4, src += src_step ) 1404 { 1405 t0 = src[0]; t1 = src[1]; 1406 dst0[i] = t0; dst0[i+1] = t1; 1407 t0 = src[2]; t1 = src[3]; 1408 dst0[i+2] = t0; dst0[i+3] = t1; 1409 t0 = src[4]; t1 = src[5]; 1410 dst1[i] = t0; dst1[i+1] = t1; 1411 t0 = src[6]; t1 = src[7]; 1412 dst1[i+2] = t0; dst1[i+3] = t1; 1413 } 1414 } 1415 } 1416 1417 1418 static void 1419 CopyTo2Columns( const uchar* _src0, const uchar* _src1, 1420 uchar* _dst, size_t dst_step, 1421 int len, size_t elem_size ) 1422 { 1423 int i, t0, t1; 1424 const int* src0 = (const int*)_src0; 1425 const int* src1 = (const int*)_src1; 1426 int* dst = (int*)_dst; 1427 dst_step /= sizeof(dst[0]); 1428 1429 if( elem_size == sizeof(int) ) 1430 { 1431 for( i = 0; i < len; i++, dst += dst_step ) 1432 { 1433 t0 = src0[i]; t1 = src1[i]; 1434 dst[0] = t0; dst[1] = t1; 1435 } 1436 } 1437 else if( elem_size == sizeof(int)*2 ) 1438 { 1439 for( i = 0; i < len*2; i += 2, dst += dst_step ) 1440 { 1441 t0 = src0[i]; t1 = src0[i+1]; 1442 dst[0] = t0; dst[1] = t1; 1443 t0 = src1[i]; t1 = src1[i+1]; 1444 dst[2] = t0; dst[3] = t1; 1445 } 1446 } 1447 else if( elem_size == sizeof(int)*4 ) 1448 { 1449 for( i = 0; i < len*4; i += 4, dst += dst_step ) 1450 { 1451 t0 = src0[i]; t1 = src0[i+1]; 1452 dst[0] = t0; dst[1] = t1; 1453 t0 = src0[i+2]; t1 = src0[i+3]; 1454 dst[2] = t0; dst[3] = t1; 1455 t0 = src1[i]; t1 = src1[i+1]; 1456 dst[4] = t0; dst[5] = t1; 1457 t0 = src1[i+2]; t1 = src1[i+3]; 1458 dst[6] = t0; dst[7] = t1; 1459 } 1460 } 1461 } 1462 1463 1464 static void 1465 ExpandCCS( uchar* _ptr, int n, int elem_size ) 1466 { 1467 int i; 1468 if( elem_size == (int)sizeof(float) ) 1469 { 1470 float* p = (float*)_ptr; 1471 for( i = 1; i < (n+1)/2; i++ ) 1472 { 1473 p[(n-i)*2] = p[i*2-1]; 1474 p[(n-i)*2+1] = -p[i*2]; 1475 } 1476 if( (n & 1) == 0 ) 1477 { 1478 p[n] = p[n-1]; 1479 p[n+1] = 0.f; 1480 n--; 1481 } 1482 for( i = n-1; i > 0; i-- ) 1483 p[i+1] = p[i]; 1484 p[1] = 0.f; 1485 } 1486 else 1487 { 1488 double* p = (double*)_ptr; 1489 for( i = 1; i < (n+1)/2; i++ ) 1490 { 1491 p[(n-i)*2] = p[i*2-1]; 1492 p[(n-i)*2+1] = -p[i*2]; 1493 } 1494 if( (n & 1) == 0 ) 1495 { 1496 p[n] = p[n-1]; 1497 p[n+1] = 0.f; 1498 n--; 1499 } 1500 for( i = n-1; i > 0; i-- ) 1501 p[i+1] = p[i]; 1502 p[1] = 0.f; 1503 } 1504 } 1505 1506 static void DFT_32f(const OcvDftOptions & c, const Complexf* src, Complexf* dst) 1507 { 1508 DFT(c, src, dst); 1509 } 1510 1511 static void DFT_64f(const OcvDftOptions & c, const Complexd* src, Complexd* dst) 1512 { 1513 DFT(c, src, dst); 1514 } 1515 1516 1517 static void RealDFT_32f(const OcvDftOptions & c, const float* src, float* dst) 1518 { 1519 RealDFT(c, src, dst); 1520 } 1521 1522 static void RealDFT_64f(const OcvDftOptions & c, const double* src, double* dst) 1523 { 1524 RealDFT(c, src, dst); 1525 } 1526 1527 static void CCSIDFT_32f(const OcvDftOptions & c, const float* src, float* dst) 1528 { 1529 CCSIDFT(c, src, dst); 1530 } 1531 1532 static void CCSIDFT_64f(const OcvDftOptions & c, const double* src, double* dst) 1533 { 1534 CCSIDFT(c, src, dst); 1535 } 1536 1537 } 1538 1539 #ifdef USE_IPP_DFT 1540 typedef IppStatus (CV_STDCALL* IppDFTGetSizeFunc)(int, int, IppHintAlgorithm, int*, int*, int*); 1541 typedef IppStatus (CV_STDCALL* IppDFTInitFunc)(int, int, IppHintAlgorithm, void*, uchar*); 1542 #endif 1543 1544 namespace cv 1545 { 1546 #if defined USE_IPP_DFT 1547 1548 typedef IppStatus (CV_STDCALL* ippiDFT_C_Func)(const Ipp32fc*, int, Ipp32fc*, int, const IppiDFTSpec_C_32fc*, Ipp8u*); 1549 typedef IppStatus (CV_STDCALL* ippiDFT_R_Func)(const Ipp32f* , int, Ipp32f* , int, const IppiDFTSpec_R_32f* , Ipp8u*); 1550 1551 template <typename Dft> 1552 class Dft_C_IPPLoop_Invoker : public ParallelLoopBody 1553 { 1554 public: 1555 1556 Dft_C_IPPLoop_Invoker(const uchar * _src, size_t _src_step, uchar * _dst, size_t _dst_step, int _width, 1557 const Dft& _ippidft, int _norm_flag, bool *_ok) : 1558 ParallelLoopBody(), 1559 src(_src), src_step(_src_step), dst(_dst), dst_step(_dst_step), width(_width), 1560 ippidft(_ippidft), norm_flag(_norm_flag), ok(_ok) 1561 { 1562 *ok = true; 1563 } 1564 1565 virtual void operator()(const Range& range) const CV_OVERRIDE 1566 { 1567 IppStatus status; 1568 Ipp8u* pBuffer = 0; 1569 Ipp8u* pMemInit= 0; 1570 int sizeBuffer=0; 1571 int sizeSpec=0; 1572 int sizeInit=0; 1573 1574 IppiSize srcRoiSize = {width, 1}; 1575 1576 status = ippiDFTGetSize_C_32fc(srcRoiSize, norm_flag, ippAlgHintNone, &sizeSpec, &sizeInit, &sizeBuffer ); 1577 if ( status < 0 ) 1578 { 1579 *ok = false; 1580 return; 1581 } 1582 1583 IppiDFTSpec_C_32fc* pDFTSpec = (IppiDFTSpec_C_32fc*)CV_IPP_MALLOC( sizeSpec ); 1584 1585 if ( sizeInit > 0 ) 1586 pMemInit = (Ipp8u*)CV_IPP_MALLOC( sizeInit ); 1587 1588 if ( sizeBuffer > 0 ) 1589 pBuffer = (Ipp8u*)CV_IPP_MALLOC( sizeBuffer ); 1590 1591 status = ippiDFTInit_C_32fc( srcRoiSize, norm_flag, ippAlgHintNone, pDFTSpec, pMemInit ); 1592 1593 if ( sizeInit > 0 ) 1594 ippFree( pMemInit ); 1595 1596 if ( status < 0 ) 1597 { 1598 ippFree( pDFTSpec ); 1599 if ( sizeBuffer > 0 ) 1600 ippFree( pBuffer ); 1601 *ok = false; 1602 return; 1603 } 1604 1605 for( int i = range.start; i < range.end; ++i) 1606 if(!ippidft((Ipp32fc*)(src + src_step * i), src_step, (Ipp32fc*)(dst + dst_step * i), dst_step, 1607 pDFTSpec, (Ipp8u*)pBuffer)) 1608 { 1609 *ok = false; 1610 } 1611 1612 if ( sizeBuffer > 0 ) 1613 ippFree( pBuffer ); 1614 1615 ippFree( pDFTSpec ); 1616 CV_IMPL_ADD(CV_IMPL_IPP|CV_IMPL_MT); 1617 } 1618 1619 private: 1620 const uchar * src; 1621 size_t src_step; 1622 uchar * dst; 1623 size_t dst_step; 1624 int width; 1625 const Dft& ippidft; 1626 int norm_flag; 1627 bool *ok; 1628 1629 const Dft_C_IPPLoop_Invoker& operator= (const Dft_C_IPPLoop_Invoker&); 1630 }; 1631 1632 template <typename Dft> 1633 class Dft_R_IPPLoop_Invoker : public ParallelLoopBody 1634 { 1635 public: 1636 1637 Dft_R_IPPLoop_Invoker(const uchar * _src, size_t _src_step, uchar * _dst, size_t _dst_step, int _width, 1638 const Dft& _ippidft, int _norm_flag, bool *_ok) : 1639 ParallelLoopBody(), 1640 src(_src), src_step(_src_step), dst(_dst), dst_step(_dst_step), width(_width), 1641 ippidft(_ippidft), norm_flag(_norm_flag), ok(_ok) 1642 { 1643 *ok = true; 1644 } 1645 1646 virtual void operator()(const Range& range) const CV_OVERRIDE 1647 { 1648 IppStatus status; 1649 Ipp8u* pBuffer = 0; 1650 Ipp8u* pMemInit= 0; 1651 int sizeBuffer=0; 1652 int sizeSpec=0; 1653 int sizeInit=0; 1654 1655 IppiSize srcRoiSize = {width, 1}; 1656 1657 status = ippiDFTGetSize_R_32f(srcRoiSize, norm_flag, ippAlgHintNone, &sizeSpec, &sizeInit, &sizeBuffer ); 1658 if ( status < 0 ) 1659 { 1660 *ok = false; 1661 return; 1662 } 1663 1664 IppiDFTSpec_R_32f* pDFTSpec = (IppiDFTSpec_R_32f*)CV_IPP_MALLOC( sizeSpec ); 1665 1666 if ( sizeInit > 0 ) 1667 pMemInit = (Ipp8u*)CV_IPP_MALLOC( sizeInit ); 1668 1669 if ( sizeBuffer > 0 ) 1670 pBuffer = (Ipp8u*)CV_IPP_MALLOC( sizeBuffer ); 1671 1672 status = ippiDFTInit_R_32f( srcRoiSize, norm_flag, ippAlgHintNone, pDFTSpec, pMemInit ); 1673 1674 if ( sizeInit > 0 ) 1675 ippFree( pMemInit ); 1676 1677 if ( status < 0 ) 1678 { 1679 ippFree( pDFTSpec ); 1680 if ( sizeBuffer > 0 ) 1681 ippFree( pBuffer ); 1682 *ok = false; 1683 return; 1684 } 1685 1686 for( int i = range.start; i < range.end; ++i) 1687 if(!ippidft((float*)(src + src_step * i), src_step, (float*)(dst + dst_step * i), dst_step, 1688 pDFTSpec, (Ipp8u*)pBuffer)) 1689 { 1690 *ok = false; 1691 } 1692 1693 if ( sizeBuffer > 0 ) 1694 ippFree( pBuffer ); 1695 1696 ippFree( pDFTSpec ); 1697 CV_IMPL_ADD(CV_IMPL_IPP|CV_IMPL_MT); 1698 } 1699 1700 private: 1701 const uchar * src; 1702 size_t src_step; 1703 uchar * dst; 1704 size_t dst_step; 1705 int width; 1706 const Dft& ippidft; 1707 int norm_flag; 1708 bool *ok; 1709 1710 const Dft_R_IPPLoop_Invoker& operator= (const Dft_R_IPPLoop_Invoker&); 1711 }; 1712 1713 template <typename Dft> 1714 bool Dft_C_IPPLoop(const uchar * src, size_t src_step, uchar * dst, size_t dst_step, int width, int height, const Dft& ippidft, int norm_flag) 1715 { 1716 bool ok; 1717 parallel_for_(Range(0, height), Dft_C_IPPLoop_Invoker<Dft>(src, src_step, dst, dst_step, width, ippidft, norm_flag, &ok), (width * height)/(double)(1<<16) ); 1718 return ok; 1719 } 1720 1721 template <typename Dft> 1722 bool Dft_R_IPPLoop(const uchar * src, size_t src_step, uchar * dst, size_t dst_step, int width, int height, const Dft& ippidft, int norm_flag) 1723 { 1724 bool ok; 1725 parallel_for_(Range(0, height), Dft_R_IPPLoop_Invoker<Dft>(src, src_step, dst, dst_step, width, ippidft, norm_flag, &ok), (width * height)/(double)(1<<16) ); 1726 return ok; 1727 } 1728 1729 struct IPPDFT_C_Functor 1730 { 1731 IPPDFT_C_Functor(ippiDFT_C_Func _func) : ippiDFT_CToC_32fc_C1R(_func){} 1732 1733 bool operator()(const Ipp32fc* src, size_t srcStep, Ipp32fc* dst, size_t dstStep, const IppiDFTSpec_C_32fc* pDFTSpec, Ipp8u* pBuffer) const 1734 { 1735 return ippiDFT_CToC_32fc_C1R ? CV_INSTRUMENT_FUN_IPP(ippiDFT_CToC_32fc_C1R, src, static_cast<int>(srcStep), dst, static_cast<int>(dstStep), pDFTSpec, pBuffer) >= 0 : false; 1736 } 1737 private: 1738 ippiDFT_C_Func ippiDFT_CToC_32fc_C1R; 1739 }; 1740 1741 struct IPPDFT_R_Functor 1742 { 1743 IPPDFT_R_Functor(ippiDFT_R_Func _func) : ippiDFT_PackToR_32f_C1R(_func){} 1744 1745 bool operator()(const Ipp32f* src, size_t srcStep, Ipp32f* dst, size_t dstStep, const IppiDFTSpec_R_32f* pDFTSpec, Ipp8u* pBuffer) const 1746 { 1747 return ippiDFT_PackToR_32f_C1R ? CV_INSTRUMENT_FUN_IPP(ippiDFT_PackToR_32f_C1R, src, static_cast<int>(srcStep), dst, static_cast<int>(dstStep), pDFTSpec, pBuffer) >= 0 : false; 1748 } 1749 private: 1750 ippiDFT_R_Func ippiDFT_PackToR_32f_C1R; 1751 }; 1752 1753 static bool ippi_DFT_C_32F(const uchar * src, size_t src_step, uchar * dst, size_t dst_step, int width, int height, bool inv, int norm_flag) 1754 { 1755 CV_INSTRUMENT_REGION_IPP(); 1756 1757 IppStatus status; 1758 Ipp8u* pBuffer = 0; 1759 Ipp8u* pMemInit= 0; 1760 int sizeBuffer=0; 1761 int sizeSpec=0; 1762 int sizeInit=0; 1763 1764 IppiSize srcRoiSize = {width, height}; 1765 1766 status = ippiDFTGetSize_C_32fc(srcRoiSize, norm_flag, ippAlgHintNone, &sizeSpec, &sizeInit, &sizeBuffer ); 1767 if ( status < 0 ) 1768 return false; 1769 1770 IppiDFTSpec_C_32fc* pDFTSpec = (IppiDFTSpec_C_32fc*)CV_IPP_MALLOC( sizeSpec ); 1771 1772 if ( sizeInit > 0 ) 1773 pMemInit = (Ipp8u*)CV_IPP_MALLOC( sizeInit ); 1774 1775 if ( sizeBuffer > 0 ) 1776 pBuffer = (Ipp8u*)CV_IPP_MALLOC( sizeBuffer ); 1777 1778 status = ippiDFTInit_C_32fc( srcRoiSize, norm_flag, ippAlgHintNone, pDFTSpec, pMemInit ); 1779 1780 if ( sizeInit > 0 ) 1781 ippFree( pMemInit ); 1782 1783 if ( status < 0 ) 1784 { 1785 ippFree( pDFTSpec ); 1786 if ( sizeBuffer > 0 ) 1787 ippFree( pBuffer ); 1788 return false; 1789 } 1790 1791 if (!inv) 1792 status = CV_INSTRUMENT_FUN_IPP(ippiDFTFwd_CToC_32fc_C1R, (Ipp32fc*)src, static_cast<int>(src_step), (Ipp32fc*)dst, static_cast<int>(dst_step), pDFTSpec, pBuffer); 1793 else 1794 status = CV_INSTRUMENT_FUN_IPP(ippiDFTInv_CToC_32fc_C1R, (Ipp32fc*)src, static_cast<int>(src_step), (Ipp32fc*)dst, static_cast<int>(dst_step), pDFTSpec, pBuffer); 1795 1796 if ( sizeBuffer > 0 ) 1797 ippFree( pBuffer ); 1798 1799 ippFree( pDFTSpec ); 1800 1801 if(status >= 0) 1802 { 1803 CV_IMPL_ADD(CV_IMPL_IPP); 1804 return true; 1805 } 1806 return false; 1807 } 1808 1809 static bool ippi_DFT_R_32F(const uchar * src, size_t src_step, uchar * dst, size_t dst_step, int width, int height, bool inv, int norm_flag) 1810 { 1811 CV_INSTRUMENT_REGION_IPP(); 1812 1813 IppStatus status; 1814 Ipp8u* pBuffer = 0; 1815 Ipp8u* pMemInit= 0; 1816 int sizeBuffer=0; 1817 int sizeSpec=0; 1818 int sizeInit=0; 1819 1820 IppiSize srcRoiSize = {width, height}; 1821 1822 status = ippiDFTGetSize_R_32f(srcRoiSize, norm_flag, ippAlgHintNone, &sizeSpec, &sizeInit, &sizeBuffer ); 1823 if ( status < 0 ) 1824 return false; 1825 1826 IppiDFTSpec_R_32f* pDFTSpec = (IppiDFTSpec_R_32f*)CV_IPP_MALLOC( sizeSpec ); 1827 1828 if ( sizeInit > 0 ) 1829 pMemInit = (Ipp8u*)CV_IPP_MALLOC( sizeInit ); 1830 1831 if ( sizeBuffer > 0 ) 1832 pBuffer = (Ipp8u*)CV_IPP_MALLOC( sizeBuffer ); 1833 1834 status = ippiDFTInit_R_32f( srcRoiSize, norm_flag, ippAlgHintNone, pDFTSpec, pMemInit ); 1835 1836 if ( sizeInit > 0 ) 1837 ippFree( pMemInit ); 1838 1839 if ( status < 0 ) 1840 { 1841 ippFree( pDFTSpec ); 1842 if ( sizeBuffer > 0 ) 1843 ippFree( pBuffer ); 1844 return false; 1845 } 1846 1847 if (!inv) 1848 status = CV_INSTRUMENT_FUN_IPP(ippiDFTFwd_RToPack_32f_C1R, (float*)src, static_cast<int>(src_step), (float*)dst, static_cast<int>(dst_step), pDFTSpec, pBuffer); 1849 else 1850 status = CV_INSTRUMENT_FUN_IPP(ippiDFTInv_PackToR_32f_C1R, (float*)src, static_cast<int>(src_step), (float*)dst, static_cast<int>(dst_step), pDFTSpec, pBuffer); 1851 1852 if ( sizeBuffer > 0 ) 1853 ippFree( pBuffer ); 1854 1855 ippFree( pDFTSpec ); 1856 1857 if(status >= 0) 1858 { 1859 CV_IMPL_ADD(CV_IMPL_IPP); 1860 return true; 1861 } 1862 return false; 1863 } 1864 1865 #endif 1866 } 1867 1868 #ifdef HAVE_OPENCL 1869 1870 namespace cv 1871 { 1872 1873 enum FftType 1874 { 1875 R2R = 0, // real to CCS in case forward transform, CCS to real otherwise 1876 C2R = 1, // complex to real in case inverse transform 1877 R2C = 2, // real to complex in case forward transform 1878 C2C = 3 // complex to complex 1879 }; 1880 1881 struct OCL_FftPlan 1882 { 1883 private: 1884 UMat twiddles; 1885 String buildOptions; 1886 int thread_count; 1887 int dft_size; 1888 int dft_depth; 1889 bool status; 1890 1891 public: 1892 OCL_FftPlan(int _size, int _depth) : dft_size(_size), dft_depth(_depth), status(true) 1893 { 1894 CV_Assert( dft_depth == CV_32F || dft_depth == CV_64F ); 1895 1896 int min_radix; 1897 std::vector<int> radixes, blocks; 1898 ocl_getRadixes(dft_size, radixes, blocks, min_radix); 1899 thread_count = dft_size / min_radix; 1900 1901 if (thread_count > (int) ocl::Device::getDefault().maxWorkGroupSize()) 1902 { 1903 status = false; 1904 return; 1905 } 1906 1907 // generate string with radix calls 1908 String radix_processing; 1909 int n = 1, twiddle_size = 0; 1910 for (size_t i=0; i<radixes.size(); i++) 1911 { 1912 int radix = radixes[i], block = blocks[i]; 1913 if (block > 1) 1914 radix_processing += format("fft_radix%d_B%d(smem,twiddles+%d,ind,%d,%d);", radix, block, twiddle_size, n, dft_size/radix); 1915 else 1916 radix_processing += format("fft_radix%d(smem,twiddles+%d,ind,%d,%d);", radix, twiddle_size, n, dft_size/radix); 1917 twiddle_size += (radix-1)*n; 1918 n *= radix; 1919 } 1920 1921 twiddles.create(1, twiddle_size, CV_MAKE_TYPE(dft_depth, 2)); 1922 if (dft_depth == CV_32F) 1923 fillRadixTable<float>(twiddles, radixes); 1924 else 1925 fillRadixTable<double>(twiddles, radixes); 1926 1927 buildOptions = format("-D LOCAL_SIZE=%d -D kercn=%d -D FT=%s -D CT=%s%s -D RADIX_PROCESS=%s", 1928 dft_size, min_radix, ocl::typeToStr(dft_depth), ocl::typeToStr(CV_MAKE_TYPE(dft_depth, 2)), 1929 dft_depth == CV_64F ? " -D DOUBLE_SUPPORT" : "", radix_processing.c_str()); 1930 } 1931 1932 bool enqueueTransform(InputArray _src, OutputArray _dst, int num_dfts, int flags, int fftType, bool rows = true) const 1933 { 1934 if (!status) 1935 return false; 1936 1937 UMat src = _src.getUMat(); 1938 UMat dst = _dst.getUMat(); 1939 1940 size_t globalsize[2]; 1941 size_t localsize[2]; 1942 String kernel_name; 1943 1944 bool is1d = (flags & DFT_ROWS) != 0 || num_dfts == 1; 1945 bool inv = (flags & DFT_INVERSE) != 0; 1946 String options = buildOptions; 1947 1948 if (rows) 1949 { 1950 globalsize[0] = thread_count; globalsize[1] = src.rows; 1951 localsize[0] = thread_count; localsize[1] = 1; 1952 kernel_name = !inv ? "fft_multi_radix_rows" : "ifft_multi_radix_rows"; 1953 if ((is1d || inv) && (flags & DFT_SCALE)) 1954 options += " -D DFT_SCALE"; 1955 } 1956 else 1957 { 1958 globalsize[0] = num_dfts; globalsize[1] = thread_count; 1959 localsize[0] = 1; localsize[1] = thread_count; 1960 kernel_name = !inv ? "fft_multi_radix_cols" : "ifft_multi_radix_cols"; 1961 if (flags & DFT_SCALE) 1962 options += " -D DFT_SCALE"; 1963 } 1964 1965 options += src.channels() == 1 ? " -D REAL_INPUT" : " -D COMPLEX_INPUT"; 1966 options += dst.channels() == 1 ? " -D REAL_OUTPUT" : " -D COMPLEX_OUTPUT"; 1967 options += is1d ? " -D IS_1D" : ""; 1968 1969 if (!inv) 1970 { 1971 if ((is1d && src.channels() == 1) || (rows && (fftType == R2R))) 1972 options += " -D NO_CONJUGATE"; 1973 } 1974 else 1975 { 1976 if (rows && (fftType == C2R || fftType == R2R)) 1977 options += " -D NO_CONJUGATE"; 1978 if (dst.cols % 2 == 0) 1979 options += " -D EVEN"; 1980 } 1981 1982 ocl::Kernel k(kernel_name.c_str(), ocl::core::fft_oclsrc, options); 1983 if (k.empty()) 1984 return false; 1985 1986 k.args(ocl::KernelArg::ReadOnly(src), ocl::KernelArg::WriteOnly(dst), ocl::KernelArg::ReadOnlyNoSize(twiddles), thread_count, num_dfts); 1987 return k.run(2, globalsize, localsize, false); 1988 } 1989 1990 private: 1991 static void ocl_getRadixes(int cols, std::vector<int>& radixes, std::vector<int>& blocks, int& min_radix) 1992 { 1993 int factors[34]; 1994 int nf = DFTFactorize(cols, factors); 1995 1996 int n = 1; 1997 int factor_index = 0; 1998 min_radix = INT_MAX; 1999 2000 // 2^n transforms 2001 if ((factors[factor_index] & 1) == 0) 2002 { 2003 for( ; n < factors[factor_index];) 2004 { 2005 int radix = 2, block = 1; 2006 if (8*n <= factors[0]) 2007 radix = 8; 2008 else if (4*n <= factors[0]) 2009 { 2010 radix = 4; 2011 if (cols % 12 == 0) 2012 block = 3; 2013 else if (cols % 8 == 0) 2014 block = 2; 2015 } 2016 else 2017 { 2018 if (cols % 10 == 0) 2019 block = 5; 2020 else if (cols % 8 == 0) 2021 block = 4; 2022 else if (cols % 6 == 0) 2023 block = 3; 2024 else if (cols % 4 == 0) 2025 block = 2; 2026 } 2027 2028 radixes.push_back(radix); 2029 blocks.push_back(block); 2030 min_radix = min(min_radix, block*radix); 2031 n *= radix; 2032 } 2033 factor_index++; 2034 } 2035 2036 // all the other transforms 2037 for( ; factor_index < nf; factor_index++) 2038 { 2039 int radix = factors[factor_index], block = 1; 2040 if (radix == 3) 2041 { 2042 if (cols % 12 == 0) 2043 block = 4; 2044 else if (cols % 9 == 0) 2045 block = 3; 2046 else if (cols % 6 == 0) 2047 block = 2; 2048 } 2049 else if (radix == 5) 2050 { 2051 if (cols % 10 == 0) 2052 block = 2; 2053 } 2054 radixes.push_back(radix); 2055 blocks.push_back(block); 2056 min_radix = min(min_radix, block*radix); 2057 } 2058 } 2059 2060 template <typename T> 2061 static void fillRadixTable(UMat twiddles, const std::vector<int>& radixes) 2062 { 2063 Mat tw = twiddles.getMat(ACCESS_WRITE); 2064 T* ptr = tw.ptr<T>(); 2065 int ptr_index = 0; 2066 2067 int n = 1; 2068 for (size_t i=0; i<radixes.size(); i++) 2069 { 2070 int radix = radixes[i]; 2071 n *= radix; 2072 2073 for (int j=1; j<radix; j++) 2074 { 2075 double theta = -CV_2PI*j/n; 2076 2077 for (int k=0; k<(n/radix); k++) 2078 { 2079 ptr[ptr_index++] = (T) cos(k*theta); 2080 ptr[ptr_index++] = (T) sin(k*theta); 2081 } 2082 } 2083 } 2084 } 2085 }; 2086 2087 class OCL_FftPlanCache 2088 { 2089 public: 2090 static OCL_FftPlanCache & getInstance() 2091 { 2092 CV_SINGLETON_LAZY_INIT_REF(OCL_FftPlanCache, new OCL_FftPlanCache()) 2093 } 2094 2095 Ptr<OCL_FftPlan> getFftPlan(int dft_size, int depth) 2096 { 2097 int key = (dft_size << 16) | (depth & 0xFFFF); 2098 std::map<int, Ptr<OCL_FftPlan> >::iterator f = planStorage.find(key); 2099 if (f != planStorage.end()) 2100 { 2101 return f->second; 2102 } 2103 else 2104 { 2105 Ptr<OCL_FftPlan> newPlan = Ptr<OCL_FftPlan>(new OCL_FftPlan(dft_size, depth)); 2106 planStorage[key] = newPlan; 2107 return newPlan; 2108 } 2109 } 2110 2111 ~OCL_FftPlanCache() 2112 { 2113 planStorage.clear(); 2114 } 2115 2116 protected: 2117 OCL_FftPlanCache() : 2118 planStorage() 2119 { 2120 } 2121 std::map<int, Ptr<OCL_FftPlan> > planStorage; 2122 }; 2123 2124 static bool ocl_dft_rows(InputArray _src, OutputArray _dst, int nonzero_rows, int flags, int fftType) 2125 { 2126 int type = _src.type(), depth = CV_MAT_DEPTH(type); 2127 Ptr<OCL_FftPlan> plan = OCL_FftPlanCache::getInstance().getFftPlan(_src.cols(), depth); 2128 return plan->enqueueTransform(_src, _dst, nonzero_rows, flags, fftType, true); 2129 } 2130 2131 static bool ocl_dft_cols(InputArray _src, OutputArray _dst, int nonzero_cols, int flags, int fftType) 2132 { 2133 int type = _src.type(), depth = CV_MAT_DEPTH(type); 2134 Ptr<OCL_FftPlan> plan = OCL_FftPlanCache::getInstance().getFftPlan(_src.rows(), depth); 2135 return plan->enqueueTransform(_src, _dst, nonzero_cols, flags, fftType, false); 2136 } 2137 2138 inline FftType determineFFTType(bool real_input, bool complex_input, bool real_output, bool complex_output, bool inv) 2139 { 2140 // output format is not specified 2141 if (!real_output && !complex_output) 2142 complex_output = true; 2143 2144 // input or output format is ambiguous 2145 if (real_input == complex_input || real_output == complex_output) 2146 CV_Error(Error::StsBadArg, "Invalid FFT input or output format"); 2147 2148 FftType result = real_input ? (real_output ? R2R : R2C) : (real_output ? C2R : C2C); 2149 2150 // Forward Complex to CCS not supported 2151 if (result == C2R && !inv) 2152 result = C2C; 2153 2154 // Inverse CCS to Complex not supported 2155 if (result == R2C && inv) 2156 result = R2R; 2157 2158 return result; 2159 } 2160 2161 static bool ocl_dft(InputArray _src, OutputArray _dst, int flags, int nonzero_rows) 2162 { 2163 int type = _src.type(), cn = CV_MAT_CN(type), depth = CV_MAT_DEPTH(type); 2164 Size ssize = _src.size(); 2165 bool doubleSupport = ocl::Device::getDefault().doubleFPConfig() > 0; 2166 2167 if (!(cn == 1 || cn == 2) 2168 || !(depth == CV_32F || (depth == CV_64F && doubleSupport)) 2169 || ((flags & DFT_REAL_OUTPUT) && (flags & DFT_COMPLEX_OUTPUT))) 2170 return false; 2171 2172 // if is not a multiplication of prime numbers { 2, 3, 5 } 2173 if (ssize.area() != getOptimalDFTSize(ssize.area())) 2174 return false; 2175 2176 UMat src = _src.getUMat(); 2177 bool inv = (flags & DFT_INVERSE) != 0 ? 1 : 0; 2178 2179 if( nonzero_rows <= 0 || nonzero_rows > _src.rows() ) 2180 nonzero_rows = _src.rows(); 2181 bool is1d = (flags & DFT_ROWS) != 0 || nonzero_rows == 1; 2182 2183 FftType fftType = determineFFTType(cn == 1, cn == 2, 2184 (flags & DFT_REAL_OUTPUT) != 0, (flags & DFT_COMPLEX_OUTPUT) != 0, inv); 2185 2186 UMat output; 2187 if (fftType == C2C || fftType == R2C) 2188 { 2189 // complex output 2190 _dst.create(src.size(), CV_MAKETYPE(depth, 2)); 2191 output = _dst.getUMat(); 2192 } 2193 else 2194 { 2195 // real output 2196 if (is1d) 2197 { 2198 _dst.create(src.size(), CV_MAKETYPE(depth, 1)); 2199 output = _dst.getUMat(); 2200 } 2201 else 2202 { 2203 _dst.create(src.size(), CV_MAKETYPE(depth, 1)); 2204 output.create(src.size(), CV_MAKETYPE(depth, 2)); 2205 } 2206 } 2207 2208 bool result = false; 2209 if (!inv) 2210 { 2211 int nonzero_cols = fftType == R2R ? output.cols/2 + 1 : output.cols; 2212 result = ocl_dft_rows(src, output, nonzero_rows, flags, fftType); 2213 if (!is1d) 2214 result = result && ocl_dft_cols(output, _dst, nonzero_cols, flags, fftType); 2215 } 2216 else 2217 { 2218 if (fftType == C2C) 2219 { 2220 // complex output 2221 result = ocl_dft_rows(src, output, nonzero_rows, flags, fftType); 2222 if (!is1d) 2223 result = result && ocl_dft_cols(output, output, output.cols, flags, fftType); 2224 } 2225 else 2226 { 2227 if (is1d) 2228 { 2229 result = ocl_dft_rows(src, output, nonzero_rows, flags, fftType); 2230 } 2231 else 2232 { 2233 int nonzero_cols = src.cols/2 + 1; 2234 result = ocl_dft_cols(src, output, nonzero_cols, flags, fftType); 2235 result = result && ocl_dft_rows(output, _dst, nonzero_rows, flags, fftType); 2236 } 2237 } 2238 } 2239 return result; 2240 } 2241 2242 } // namespace cv; 2243 2244 #endif 2245 2246 #ifdef HAVE_CLAMDFFT 2247 2248 namespace cv { 2249 2250 #define CLAMDDFT_Assert(func) \ 2251 { \ 2252 clAmdFftStatus s = (func); \ 2253 CV_Assert(s == CLFFT_SUCCESS); \ 2254 } 2255 2256 class PlanCache 2257 { 2258 struct FftPlan 2259 { 2260 FftPlan(const Size & _dft_size, int _src_step, int _dst_step, bool _doubleFP, bool _inplace, int _flags, FftType _fftType) : 2261 dft_size(_dft_size), src_step(_src_step), dst_step(_dst_step), 2262 doubleFP(_doubleFP), inplace(_inplace), flags(_flags), fftType(_fftType), 2263 context((cl_context)ocl::Context::getDefault().ptr()), plHandle(0) 2264 { 2265 bool dft_inverse = (flags & DFT_INVERSE) != 0; 2266 bool dft_scale = (flags & DFT_SCALE) != 0; 2267 bool dft_rows = (flags & DFT_ROWS) != 0; 2268 2269 clAmdFftLayout inLayout = CLFFT_REAL, outLayout = CLFFT_REAL; 2270 clAmdFftDim dim = dft_size.height == 1 || dft_rows ? CLFFT_1D : CLFFT_2D; 2271 2272 size_t batchSize = dft_rows ? dft_size.height : 1; 2273 size_t clLengthsIn[3] = { (size_t)dft_size.width, dft_rows ? 1 : (size_t)dft_size.height, 1 }; 2274 size_t clStridesIn[3] = { 1, 1, 1 }; 2275 size_t clStridesOut[3] = { 1, 1, 1 }; 2276 int elemSize = doubleFP ? sizeof(double) : sizeof(float); 2277 2278 switch (fftType) 2279 { 2280 case C2C: 2281 inLayout = CLFFT_COMPLEX_INTERLEAVED; 2282 outLayout = CLFFT_COMPLEX_INTERLEAVED; 2283 clStridesIn[1] = src_step / (elemSize << 1); 2284 clStridesOut[1] = dst_step / (elemSize << 1); 2285 break; 2286 case R2C: 2287 inLayout = CLFFT_REAL; 2288 outLayout = CLFFT_HERMITIAN_INTERLEAVED; 2289 clStridesIn[1] = src_step / elemSize; 2290 clStridesOut[1] = dst_step / (elemSize << 1); 2291 break; 2292 case C2R: 2293 inLayout = CLFFT_HERMITIAN_INTERLEAVED; 2294 outLayout = CLFFT_REAL; 2295 clStridesIn[1] = src_step / (elemSize << 1); 2296 clStridesOut[1] = dst_step / elemSize; 2297 break; 2298 case R2R: 2299 default: 2300 CV_Error(Error::StsNotImplemented, "AMD Fft does not support this type"); 2301 break; 2302 } 2303 2304 clStridesIn[2] = dft_rows ? clStridesIn[1] : dft_size.width * clStridesIn[1]; 2305 clStridesOut[2] = dft_rows ? clStridesOut[1] : dft_size.width * clStridesOut[1]; 2306 2307 CLAMDDFT_Assert(clAmdFftCreateDefaultPlan(&plHandle, (cl_context)ocl::Context::getDefault().ptr(), dim, clLengthsIn)) 2308 2309 // setting plan properties 2310 CLAMDDFT_Assert(clAmdFftSetPlanPrecision(plHandle, doubleFP ? CLFFT_DOUBLE : CLFFT_SINGLE)); 2311 CLAMDDFT_Assert(clAmdFftSetResultLocation(plHandle, inplace ? CLFFT_INPLACE : CLFFT_OUTOFPLACE)) 2312 CLAMDDFT_Assert(clAmdFftSetLayout(plHandle, inLayout, outLayout)) 2313 CLAMDDFT_Assert(clAmdFftSetPlanBatchSize(plHandle, batchSize)) 2314 CLAMDDFT_Assert(clAmdFftSetPlanInStride(plHandle, dim, clStridesIn)) 2315 CLAMDDFT_Assert(clAmdFftSetPlanOutStride(plHandle, dim, clStridesOut)) 2316 CLAMDDFT_Assert(clAmdFftSetPlanDistance(plHandle, clStridesIn[dim], clStridesOut[dim])) 2317 2318 float scale = dft_scale ? 1.0f / (dft_rows ? dft_size.width : dft_size.area()) : 1.0f; 2319 CLAMDDFT_Assert(clAmdFftSetPlanScale(plHandle, dft_inverse ? CLFFT_BACKWARD : CLFFT_FORWARD, scale)) 2320 2321 // ready to bake 2322 cl_command_queue queue = (cl_command_queue)ocl::Queue::getDefault().ptr(); 2323 CLAMDDFT_Assert(clAmdFftBakePlan(plHandle, 1, &queue, NULL, NULL)) 2324 } 2325 2326 ~FftPlan() 2327 { 2328 // clAmdFftDestroyPlan(&plHandle); 2329 } 2330 2331 friend class PlanCache; 2332 2333 private: 2334 Size dft_size; 2335 int src_step, dst_step; 2336 bool doubleFP; 2337 bool inplace; 2338 int flags; 2339 FftType fftType; 2340 2341 cl_context context; 2342 clAmdFftPlanHandle plHandle; 2343 }; 2344 2345 public: 2346 static PlanCache & getInstance() 2347 { 2348 CV_SINGLETON_LAZY_INIT_REF(PlanCache, new PlanCache()) 2349 } 2350 2351 clAmdFftPlanHandle getPlanHandle(const Size & dft_size, int src_step, int dst_step, bool doubleFP, 2352 bool inplace, int flags, FftType fftType) 2353 { 2354 cl_context currentContext = (cl_context)ocl::Context::getDefault().ptr(); 2355 2356 for (size_t i = 0, size = planStorage.size(); i < size; ++i) 2357 { 2358 const FftPlan * const plan = planStorage[i]; 2359 2360 if (plan->dft_size == dft_size && 2361 plan->flags == flags && 2362 plan->src_step == src_step && 2363 plan->dst_step == dst_step && 2364 plan->doubleFP == doubleFP && 2365 plan->fftType == fftType && 2366 plan->inplace == inplace) 2367 { 2368 if (plan->context != currentContext) 2369 { 2370 planStorage.erase(planStorage.begin() + i); 2371 break; 2372 } 2373 2374 return plan->plHandle; 2375 } 2376 } 2377 2378 // no baked plan is found, so let's create a new one 2379 Ptr<FftPlan> newPlan = Ptr<FftPlan>(new FftPlan(dft_size, src_step, dst_step, doubleFP, inplace, flags, fftType)); 2380 planStorage.push_back(newPlan); 2381 2382 return newPlan->plHandle; 2383 } 2384 2385 ~PlanCache() 2386 { 2387 planStorage.clear(); 2388 } 2389 2390 protected: 2391 PlanCache() : 2392 planStorage() 2393 { 2394 } 2395 2396 std::vector<Ptr<FftPlan> > planStorage; 2397 }; 2398 2399 extern "C" { 2400 2401 static void CL_CALLBACK oclCleanupCallback(cl_event e, cl_int, void *p) 2402 { 2403 UMatData * u = (UMatData *)p; 2404 2405 if( u && CV_XADD(&u->urefcount, -1) == 1 ) 2406 u->currAllocator->deallocate(u); 2407 u = 0; 2408 2409 clReleaseEvent(e), e = 0; 2410 } 2411 2412 } 2413 2414 static bool ocl_dft_amdfft(InputArray _src, OutputArray _dst, int flags) 2415 { 2416 int type = _src.type(), depth = CV_MAT_DEPTH(type), cn = CV_MAT_CN(type); 2417 Size ssize = _src.size(); 2418 2419 bool doubleSupport = ocl::Device::getDefault().doubleFPConfig() > 0; 2420 if ( (!doubleSupport && depth == CV_64F) || 2421 !(type == CV_32FC1 || type == CV_32FC2 || type == CV_64FC1 || type == CV_64FC2) || 2422 _src.offset() != 0) 2423 return false; 2424 2425 // if is not a multiplication of prime numbers { 2, 3, 5 } 2426 if (ssize.area() != getOptimalDFTSize(ssize.area())) 2427 return false; 2428 2429 int dst_complex_input = cn == 2 ? 1 : 0; 2430 bool dft_inverse = (flags & DFT_INVERSE) != 0 ? 1 : 0; 2431 int dft_complex_output = (flags & DFT_COMPLEX_OUTPUT) != 0; 2432 bool dft_real_output = (flags & DFT_REAL_OUTPUT) != 0; 2433 2434 CV_Assert(dft_complex_output + dft_real_output < 2); 2435 FftType fftType = (FftType)(dst_complex_input << 0 | dft_complex_output << 1); 2436 2437 switch (fftType) 2438 { 2439 case C2C: 2440 _dst.create(ssize.height, ssize.width, CV_MAKE_TYPE(depth, 2)); 2441 break; 2442 case R2C: // TODO implement it if possible 2443 case C2R: // TODO implement it if possible 2444 case R2R: // AMD Fft does not support this type 2445 default: 2446 return false; 2447 } 2448 2449 UMat src = _src.getUMat(), dst = _dst.getUMat(); 2450 bool inplace = src.u == dst.u; 2451 2452 clAmdFftPlanHandle plHandle = PlanCache::getInstance(). 2453 getPlanHandle(ssize, (int)src.step, (int)dst.step, 2454 depth == CV_64F, inplace, flags, fftType); 2455 2456 // get the bufferSize 2457 size_t bufferSize = 0; 2458 CLAMDDFT_Assert(clAmdFftGetTmpBufSize(plHandle, &bufferSize)) 2459 UMat tmpBuffer(1, (int)bufferSize, CV_8UC1); 2460 2461 cl_mem srcarg = (cl_mem)src.handle(ACCESS_READ); 2462 cl_mem dstarg = (cl_mem)dst.handle(ACCESS_RW); 2463 2464 cl_command_queue queue = (cl_command_queue)ocl::Queue::getDefault().ptr(); 2465 cl_event e = 0; 2466 2467 CLAMDDFT_Assert(clAmdFftEnqueueTransform(plHandle, dft_inverse ? CLFFT_BACKWARD : CLFFT_FORWARD, 2468 1, &queue, 0, NULL, &e, 2469 &srcarg, &dstarg, (cl_mem)tmpBuffer.handle(ACCESS_RW))) 2470 2471 tmpBuffer.addref(); 2472 clSetEventCallback(e, CL_COMPLETE, oclCleanupCallback, tmpBuffer.u); 2473 return true; 2474 } 2475 2476 #undef DFT_ASSERT 2477 2478 } 2479 2480 #endif // HAVE_CLAMDFFT 2481 2482 namespace cv 2483 { 2484 2485 template <typename T> 2486 static void complementComplex(T * ptr, size_t step, int n, int len, int dft_dims) 2487 { 2488 T* p0 = (T*)ptr; 2489 size_t dstep = step/sizeof(p0[0]); 2490 for(int i = 0; i < len; i++ ) 2491 { 2492 T* p = p0 + dstep*i; 2493 T* q = dft_dims == 1 || i == 0 || i*2 == len ? p : p0 + dstep*(len-i); 2494 2495 for( int j = 1; j < (n+1)/2; j++ ) 2496 { 2497 p[(n-j)*2] = q[j*2]; 2498 p[(n-j)*2+1] = -q[j*2+1]; 2499 } 2500 } 2501 } 2502 2503 static void complementComplexOutput(int depth, uchar * ptr, size_t step, int count, int len, int dft_dims) 2504 { 2505 if( depth == CV_32F ) 2506 complementComplex((float*)ptr, step, count, len, dft_dims); 2507 else 2508 complementComplex((double*)ptr, step, count, len, dft_dims); 2509 } 2510 2511 enum DftMode { 2512 InvalidDft = 0, 2513 FwdRealToCCS, 2514 FwdRealToComplex, 2515 FwdComplexToComplex, 2516 InvCCSToReal, 2517 InvComplexToReal, 2518 InvComplexToComplex, 2519 }; 2520 2521 enum DftDims { 2522 InvalidDim = 0, 2523 OneDim, 2524 OneDimColWise, 2525 TwoDims 2526 }; 2527 2528 inline const char * modeName(DftMode m) 2529 { 2530 switch (m) 2531 { 2532 case InvalidDft: return "InvalidDft"; 2533 case FwdRealToCCS: return "FwdRealToCCS"; 2534 case FwdRealToComplex: return "FwdRealToComplex"; 2535 case FwdComplexToComplex: return "FwdComplexToComplex"; 2536 case InvCCSToReal: return "InvCCSToReal"; 2537 case InvComplexToReal: return "InvComplexToReal"; 2538 case InvComplexToComplex: return "InvComplexToComplex"; 2539 } 2540 return 0; 2541 } 2542 2543 inline const char * dimsName(DftDims d) 2544 { 2545 switch (d) 2546 { 2547 case InvalidDim: return "InvalidDim"; 2548 case OneDim: return "OneDim"; 2549 case OneDimColWise: return "OneDimColWise"; 2550 case TwoDims: return "TwoDims"; 2551 }; 2552 return 0; 2553 } 2554 2555 template <typename T> 2556 inline bool isInv(T mode) 2557 { 2558 switch ((DftMode)mode) 2559 { 2560 case InvCCSToReal: 2561 case InvComplexToReal: 2562 case InvComplexToComplex: return true; 2563 default: return false; 2564 } 2565 } 2566 2567 inline DftMode determineMode(bool inv, int cn1, int cn2) 2568 { 2569 if (!inv) 2570 { 2571 if (cn1 == 1 && cn2 == 1) 2572 return FwdRealToCCS; 2573 else if (cn1 == 1 && cn2 == 2) 2574 return FwdRealToComplex; 2575 else if (cn1 == 2 && cn2 == 2) 2576 return FwdComplexToComplex; 2577 } 2578 else 2579 { 2580 if (cn1 == 1 && cn2 == 1) 2581 return InvCCSToReal; 2582 else if (cn1 == 2 && cn2 == 1) 2583 return InvComplexToReal; 2584 else if (cn1 == 2 && cn2 == 2) 2585 return InvComplexToComplex; 2586 } 2587 return InvalidDft; 2588 } 2589 2590 2591 inline DftDims determineDims(int rows, int cols, bool isRowWise, bool isContinuous) 2592 { 2593 // printf("%d x %d (%d, %d)\n", rows, cols, isRowWise, isContinuous); 2594 if (isRowWise) 2595 return OneDim; 2596 if (cols == 1 && rows > 1) // one-column-shaped input 2597 { 2598 if (isContinuous) 2599 return OneDim; 2600 else 2601 return OneDimColWise; 2602 } 2603 if (rows == 1) 2604 return OneDim; 2605 if (cols > 1 && rows > 1) 2606 return TwoDims; 2607 return InvalidDim; 2608 } 2609 2610 class OcvDftImpl CV_FINAL : public hal::DFT2D 2611 { 2612 protected: 2613 Ptr<hal::DFT1D> contextA; 2614 Ptr<hal::DFT1D> contextB; 2615 bool needBufferA; 2616 bool needBufferB; 2617 bool inv; 2618 int width; 2619 int height; 2620 DftMode mode; 2621 int elem_size; 2622 int complex_elem_size; 2623 int depth; 2624 bool real_transform; 2625 int nonzero_rows; 2626 bool isRowTransform; 2627 bool isScaled; 2628 std::vector<int> stages; 2629 bool useIpp; 2630 int src_channels; 2631 int dst_channels; 2632 2633 AutoBuffer<uchar> tmp_bufA; 2634 AutoBuffer<uchar> tmp_bufB; 2635 AutoBuffer<uchar> buf0; 2636 AutoBuffer<uchar> buf1; 2637 2638 public: 2639 OcvDftImpl() 2640 { 2641 needBufferA = false; 2642 needBufferB = false; 2643 inv = false; 2644 width = 0; 2645 height = 0; 2646 mode = InvalidDft; 2647 elem_size = 0; 2648 complex_elem_size = 0; 2649 depth = 0; 2650 real_transform = false; 2651 nonzero_rows = 0; 2652 isRowTransform = false; 2653 isScaled = false; 2654 useIpp = false; 2655 src_channels = 0; 2656 dst_channels = 0; 2657 } 2658 2659 void init(int _width, int _height, int _depth, int _src_channels, int _dst_channels, int flags, int _nonzero_rows) 2660 { 2661 bool isComplex = _src_channels != _dst_channels; 2662 nonzero_rows = _nonzero_rows; 2663 width = _width; 2664 height = _height; 2665 depth = _depth; 2666 src_channels = _src_channels; 2667 dst_channels = _dst_channels; 2668 bool isInverse = (flags & CV_HAL_DFT_INVERSE) != 0; 2669 bool isInplace = (flags & CV_HAL_DFT_IS_INPLACE) != 0; 2670 bool isContinuous = (flags & CV_HAL_DFT_IS_CONTINUOUS) != 0; 2671 mode = determineMode(isInverse, _src_channels, _dst_channels); 2672 inv = isInverse; 2673 isRowTransform = (flags & CV_HAL_DFT_ROWS) != 0; 2674 isScaled = (flags & CV_HAL_DFT_SCALE) != 0; 2675 needBufferA = false; 2676 needBufferB = false; 2677 real_transform = (mode != FwdComplexToComplex && mode != InvComplexToComplex); 2678 2679 elem_size = (depth == CV_32F) ? sizeof(float) : sizeof(double); 2680 complex_elem_size = elem_size * 2; 2681 if( !real_transform ) 2682 elem_size = complex_elem_size; 2683 2684 #if defined USE_IPP_DFT 2685 CV_IPP_CHECK() 2686 { 2687 if (nonzero_rows == 0 && depth == CV_32F && ((width * height)>(int)(1<<6))) 2688 { 2689 if (mode == FwdComplexToComplex || mode == InvComplexToComplex || mode == FwdRealToCCS || mode == InvCCSToReal) 2690 { 2691 useIpp = true; 2692 return; 2693 } 2694 } 2695 } 2696 #endif 2697 2698 DftDims dims = determineDims(height, width, isRowTransform, isContinuous); 2699 if (dims == TwoDims) 2700 { 2701 stages.resize(2); 2702 if (mode == InvCCSToReal || mode == InvComplexToReal) 2703 { 2704 stages[0] = 1; 2705 stages[1] = 0; 2706 } 2707 else 2708 { 2709 stages[0] = 0; 2710 stages[1] = 1; 2711 } 2712 } 2713 else 2714 { 2715 stages.resize(1); 2716 if (dims == OneDimColWise) 2717 stages[0] = 1; 2718 else 2719 stages[0] = 0; 2720 } 2721 2722 for(uint stageIndex = 0; stageIndex < stages.size(); ++stageIndex) 2723 { 2724 if (stageIndex == 1) 2725 { 2726 isInplace = true; 2727 isComplex = false; 2728 } 2729 2730 int stage = stages[stageIndex]; 2731 bool isLastStage = (stageIndex + 1 == stages.size()); 2732 2733 int len, count; 2734 2735 int f = 0; 2736 if (inv) 2737 f |= CV_HAL_DFT_INVERSE; 2738 if (isScaled) 2739 f |= CV_HAL_DFT_SCALE; 2740 if (isRowTransform) 2741 f |= CV_HAL_DFT_ROWS; 2742 if (isComplex) 2743 f |= CV_HAL_DFT_COMPLEX_OUTPUT; 2744 if (real_transform) 2745 f |= CV_HAL_DFT_REAL_OUTPUT; 2746 if (!isLastStage) 2747 f |= CV_HAL_DFT_TWO_STAGE; 2748 2749 if( stage == 0 ) // row-wise transform 2750 { 2751 if (width == 1 && !isRowTransform ) 2752 { 2753 len = height; 2754 count = width; 2755 } 2756 else 2757 { 2758 len = width; 2759 count = height; 2760 } 2761 needBufferA = isInplace; 2762 contextA = hal::DFT1D::create(len, count, depth, f, &needBufferA); 2763 if (needBufferA) 2764 tmp_bufA.allocate(len * complex_elem_size); 2765 } 2766 else 2767 { 2768 len = height; 2769 count = width; 2770 f |= CV_HAL_DFT_STAGE_COLS; 2771 needBufferB = isInplace; 2772 contextB = hal::DFT1D::create(len, count, depth, f, &needBufferB); 2773 if (needBufferB) 2774 tmp_bufB.allocate(len * complex_elem_size); 2775 2776 buf0.allocate(len * complex_elem_size); 2777 buf1.allocate(len * complex_elem_size); 2778 } 2779 } 2780 } 2781 2782 void apply(const uchar * src, size_t src_step, uchar * dst, size_t dst_step) CV_OVERRIDE 2783 { 2784 #if defined USE_IPP_DFT 2785 if (useIpp) 2786 { 2787 int ipp_norm_flag = !isScaled ? 8 : inv ? 2 : 1; 2788 if (!isRowTransform) 2789 { 2790 if (mode == FwdComplexToComplex || mode == InvComplexToComplex) 2791 { 2792 if (ippi_DFT_C_32F(src, src_step, dst, dst_step, width, height, inv, ipp_norm_flag)) 2793 { 2794 CV_IMPL_ADD(CV_IMPL_IPP); 2795 return; 2796 } 2797 setIppErrorStatus(); 2798 } 2799 else if (mode == FwdRealToCCS || mode == InvCCSToReal) 2800 { 2801 if (ippi_DFT_R_32F(src, src_step, dst, dst_step, width, height, inv, ipp_norm_flag)) 2802 { 2803 CV_IMPL_ADD(CV_IMPL_IPP); 2804 return; 2805 } 2806 setIppErrorStatus(); 2807 } 2808 } 2809 else 2810 { 2811 if (mode == FwdComplexToComplex || mode == InvComplexToComplex) 2812 { 2813 ippiDFT_C_Func ippiFunc = inv ? (ippiDFT_C_Func)ippiDFTInv_CToC_32fc_C1R : (ippiDFT_C_Func)ippiDFTFwd_CToC_32fc_C1R; 2814 if (Dft_C_IPPLoop(src, src_step, dst, dst_step, width, height, IPPDFT_C_Functor(ippiFunc),ipp_norm_flag)) 2815 { 2816 CV_IMPL_ADD(CV_IMPL_IPP|CV_IMPL_MT); 2817 return; 2818 } 2819 setIppErrorStatus(); 2820 } 2821 else if (mode == FwdRealToCCS || mode == InvCCSToReal) 2822 { 2823 ippiDFT_R_Func ippiFunc = inv ? (ippiDFT_R_Func)ippiDFTInv_PackToR_32f_C1R : (ippiDFT_R_Func)ippiDFTFwd_RToPack_32f_C1R; 2824 if (Dft_R_IPPLoop(src, src_step, dst, dst_step, width, height, IPPDFT_R_Functor(ippiFunc),ipp_norm_flag)) 2825 { 2826 CV_IMPL_ADD(CV_IMPL_IPP|CV_IMPL_MT); 2827 return; 2828 } 2829 setIppErrorStatus(); 2830 } 2831 } 2832 return; 2833 } 2834 #endif 2835 2836 for(uint stageIndex = 0; stageIndex < stages.size(); ++stageIndex) 2837 { 2838 int stage_src_channels = src_channels; 2839 int stage_dst_channels = dst_channels; 2840 2841 if (stageIndex == 1) 2842 { 2843 src = dst; 2844 src_step = dst_step; 2845 stage_src_channels = stage_dst_channels; 2846 } 2847 2848 int stage = stages[stageIndex]; 2849 bool isLastStage = (stageIndex + 1 == stages.size()); 2850 bool isComplex = stage_src_channels != stage_dst_channels; 2851 2852 if( stage == 0 ) 2853 rowDft(src, src_step, dst, dst_step, isComplex, isLastStage); 2854 else 2855 colDft(src, src_step, dst, dst_step, stage_src_channels, stage_dst_channels, isLastStage); 2856 } 2857 } 2858 2859 protected: 2860 2861 void rowDft(const uchar* src_data, size_t src_step, uchar* dst_data, size_t dst_step, bool isComplex, bool isLastStage) 2862 { 2863 int len, count; 2864 if (width == 1 && !isRowTransform ) 2865 { 2866 len = height; 2867 count = width; 2868 } 2869 else 2870 { 2871 len = width; 2872 count = height; 2873 } 2874 int dptr_offset = 0; 2875 int dst_full_len = len*elem_size; 2876 2877 if( needBufferA ) 2878 { 2879 if (mode == FwdRealToCCS && (len & 1) && len > 1) 2880 dptr_offset = elem_size; 2881 } 2882 2883 if( !inv && isComplex ) 2884 dst_full_len += (len & 1) ? elem_size : complex_elem_size; 2885 2886 int nz = nonzero_rows; 2887 if( nz <= 0 || nz > count ) 2888 nz = count; 2889 2890 int i; 2891 for( i = 0; i < nz; i++ ) 2892 { 2893 const uchar* sptr = src_data + src_step * i; 2894 uchar* dptr0 = dst_data + dst_step * i; 2895 uchar* dptr = dptr0; 2896 2897 if( needBufferA ) 2898 dptr = tmp_bufA.data(); 2899 2900 contextA->apply(sptr, dptr); 2901 2902 if( needBufferA ) 2903 memcpy( dptr0, dptr + dptr_offset, dst_full_len ); 2904 } 2905 2906 for( ; i < count; i++ ) 2907 { 2908 uchar* dptr0 = dst_data + dst_step * i; 2909 memset( dptr0, 0, dst_full_len ); 2910 } 2911 if(isLastStage && mode == FwdRealToComplex) 2912 complementComplexOutput(depth, dst_data, dst_step, len, nz, 1); 2913 } 2914 2915 void colDft(const uchar* src_data, size_t src_step, uchar* dst_data, size_t dst_step, int stage_src_channels, int stage_dst_channels, bool isLastStage) 2916 { 2917 int len = height; 2918 int count = width; 2919 int a = 0, b = count; 2920 uchar *dbuf0, *dbuf1; 2921 const uchar* sptr0 = src_data; 2922 uchar* dptr0 = dst_data; 2923 2924 dbuf0 = buf0.data(), dbuf1 = buf1.data(); 2925 2926 if( needBufferB ) 2927 { 2928 dbuf1 = tmp_bufB.data(); 2929 dbuf0 = buf1.data(); 2930 } 2931 2932 if( real_transform ) 2933 { 2934 int even; 2935 a = 1; 2936 even = (count & 1) == 0; 2937 b = (count+1)/2; 2938 if( !inv ) 2939 { 2940 memset( buf0.data(), 0, len*complex_elem_size ); 2941 CopyColumn( sptr0, src_step, buf0.data(), complex_elem_size, len, elem_size ); 2942 sptr0 += stage_dst_channels*elem_size; 2943 if( even ) 2944 { 2945 memset( buf1.data(), 0, len*complex_elem_size ); 2946 CopyColumn( sptr0 + (count-2)*elem_size, src_step, 2947 buf1.data(), complex_elem_size, len, elem_size ); 2948 } 2949 } 2950 else if( stage_src_channels == 1 ) 2951 { 2952 CopyColumn( sptr0, src_step, buf0.data(), elem_size, len, elem_size ); 2953 ExpandCCS( buf0.data(), len, elem_size ); 2954 if( even ) 2955 { 2956 CopyColumn( sptr0 + (count-1)*elem_size, src_step, 2957 buf1.data(), elem_size, len, elem_size ); 2958 ExpandCCS( buf1.data(), len, elem_size ); 2959 } 2960 sptr0 += elem_size; 2961 } 2962 else 2963 { 2964 CopyColumn( sptr0, src_step, buf0.data(), complex_elem_size, len, complex_elem_size ); 2965 if( even ) 2966 { 2967 CopyColumn( sptr0 + b*complex_elem_size, src_step, 2968 buf1.data(), complex_elem_size, len, complex_elem_size ); 2969 } 2970 sptr0 += complex_elem_size; 2971 } 2972 2973 if( even ) 2974 contextB->apply(buf1.data(), dbuf1); 2975 contextB->apply(buf0.data(), dbuf0); 2976 2977 if( stage_dst_channels == 1 ) 2978 { 2979 if( !inv ) 2980 { 2981 // copy the half of output vector to the first/last column. 2982 // before doing that, defgragment the vector 2983 memcpy( dbuf0 + elem_size, dbuf0, elem_size ); 2984 CopyColumn( dbuf0 + elem_size, elem_size, dptr0, 2985 dst_step, len, elem_size ); 2986 if( even ) 2987 { 2988 memcpy( dbuf1 + elem_size, dbuf1, elem_size ); 2989 CopyColumn( dbuf1 + elem_size, elem_size, 2990 dptr0 + (count-1)*elem_size, 2991 dst_step, len, elem_size ); 2992 } 2993 dptr0 += elem_size; 2994 } 2995 else 2996 { 2997 // copy the real part of the complex vector to the first/last column 2998 CopyColumn( dbuf0, complex_elem_size, dptr0, dst_step, len, elem_size ); 2999 if( even ) 3000 CopyColumn( dbuf1, complex_elem_size, dptr0 + (count-1)*elem_size, 3001 dst_step, len, elem_size ); 3002 dptr0 += elem_size; 3003 } 3004 } 3005 else 3006 { 3007 assert( !inv ); 3008 CopyColumn( dbuf0, complex_elem_size, dptr0, 3009 dst_step, len, complex_elem_size ); 3010 if( even ) 3011 CopyColumn( dbuf1, complex_elem_size, 3012 dptr0 + b*complex_elem_size, 3013 dst_step, len, complex_elem_size ); 3014 dptr0 += complex_elem_size; 3015 } 3016 } 3017 3018 for(int i = a; i < b; i += 2 ) 3019 { 3020 if( i+1 < b ) 3021 { 3022 CopyFrom2Columns( sptr0, src_step, buf0.data(), buf1.data(), len, complex_elem_size ); 3023 contextB->apply(buf1.data(), dbuf1); 3024 } 3025 else 3026 CopyColumn( sptr0, src_step, buf0.data(), complex_elem_size, len, complex_elem_size ); 3027 3028 contextB->apply(buf0.data(), dbuf0); 3029 3030 if( i+1 < b ) 3031 CopyTo2Columns( dbuf0, dbuf1, dptr0, dst_step, len, complex_elem_size ); 3032 else 3033 CopyColumn( dbuf0, complex_elem_size, dptr0, dst_step, len, complex_elem_size ); 3034 sptr0 += 2*complex_elem_size; 3035 dptr0 += 2*complex_elem_size; 3036 } 3037 if(isLastStage && mode == FwdRealToComplex) 3038 complementComplexOutput(depth, dst_data, dst_step, count, len, 2); 3039 } 3040 }; 3041 3042 class OcvDftBasicImpl CV_FINAL : public hal::DFT1D 3043 { 3044 public: 3045 OcvDftOptions opt; 3046 int _factors[34]; 3047 AutoBuffer<uchar> wave_buf; 3048 AutoBuffer<int> itab_buf; 3049 #ifdef USE_IPP_DFT 3050 AutoBuffer<uchar> ippbuf; 3051 AutoBuffer<uchar> ippworkbuf; 3052 #endif 3053 3054 public: 3055 OcvDftBasicImpl() 3056 { 3057 opt.factors = _factors; 3058 } 3059 void init(int len, int count, int depth, int flags, bool *needBuffer) 3060 { 3061 int prev_len = opt.n; 3062 3063 int stage = (flags & CV_HAL_DFT_STAGE_COLS) != 0 ? 1 : 0; 3064 int complex_elem_size = depth == CV_32F ? sizeof(Complex<float>) : sizeof(Complex<double>); 3065 opt.isInverse = (flags & CV_HAL_DFT_INVERSE) != 0; 3066 bool real_transform = (flags & CV_HAL_DFT_REAL_OUTPUT) != 0; 3067 opt.isComplex = (stage == 0) && (flags & CV_HAL_DFT_COMPLEX_OUTPUT) != 0; 3068 bool needAnotherStage = (flags & CV_HAL_DFT_TWO_STAGE) != 0; 3069 3070 opt.scale = 1; 3071 opt.tab_size = len; 3072 opt.n = len; 3073 3074 opt.useIpp = false; 3075 #ifdef USE_IPP_DFT 3076 opt.ipp_spec = 0; 3077 opt.ipp_work = 0; 3078 3079 if( CV_IPP_CHECK_COND && (opt.n*count >= 64) ) // use IPP DFT if available 3080 { 3081 int ipp_norm_flag = (flags & CV_HAL_DFT_SCALE) == 0 ? 8 : opt.isInverse ? 2 : 1; 3082 int specsize=0, initsize=0, worksize=0; 3083 IppDFTGetSizeFunc getSizeFunc = 0; 3084 IppDFTInitFunc initFunc = 0; 3085 3086 if( real_transform && stage == 0 ) 3087 { 3088 if( depth == CV_32F ) 3089 { 3090 getSizeFunc = ippsDFTGetSize_R_32f; 3091 initFunc = (IppDFTInitFunc)ippsDFTInit_R_32f; 3092 } 3093 else 3094 { 3095 getSizeFunc = ippsDFTGetSize_R_64f; 3096 initFunc = (IppDFTInitFunc)ippsDFTInit_R_64f; 3097 } 3098 } 3099 else 3100 { 3101 if( depth == CV_32F ) 3102 { 3103 getSizeFunc = ippsDFTGetSize_C_32fc; 3104 initFunc = (IppDFTInitFunc)ippsDFTInit_C_32fc; 3105 } 3106 else 3107 { 3108 getSizeFunc = ippsDFTGetSize_C_64fc; 3109 initFunc = (IppDFTInitFunc)ippsDFTInit_C_64fc; 3110 } 3111 } 3112 if( getSizeFunc(opt.n, ipp_norm_flag, ippAlgHintNone, &specsize, &initsize, &worksize) >= 0 ) 3113 { 3114 ippbuf.allocate(specsize + initsize + 64); 3115 opt.ipp_spec = alignPtr(&ippbuf[0], 32); 3116 ippworkbuf.allocate(worksize + 32); 3117 opt.ipp_work = alignPtr(&ippworkbuf[0], 32); 3118 uchar* initbuf = alignPtr((uchar*)opt.ipp_spec + specsize, 32); 3119 if( initFunc(opt.n, ipp_norm_flag, ippAlgHintNone, opt.ipp_spec, initbuf) >= 0 ) 3120 opt.useIpp = true; 3121 } 3122 else 3123 setIppErrorStatus(); 3124 } 3125 #endif 3126 3127 if (!opt.useIpp) 3128 { 3129 if (len != prev_len) 3130 { 3131 opt.nf = DFTFactorize( opt.n, opt.factors ); 3132 } 3133 bool inplace_transform = opt.factors[0] == opt.factors[opt.nf-1]; 3134 if (len != prev_len || (!inplace_transform && opt.isInverse && real_transform)) 3135 { 3136 wave_buf.allocate(opt.n*complex_elem_size); 3137 opt.wave = wave_buf.data(); 3138 itab_buf.allocate(opt.n); 3139 opt.itab = itab_buf.data(); 3140 DFTInit( opt.n, opt.nf, opt.factors, opt.itab, complex_elem_size, 3141 opt.wave, stage == 0 && opt.isInverse && real_transform ); 3142 } 3143 // otherwise reuse the tables calculated on the previous stage 3144 if (needBuffer) 3145 { 3146 if( (stage == 0 && ((*needBuffer && !inplace_transform) || (real_transform && (len & 1)))) || 3147 (stage == 1 && !inplace_transform) ) 3148 { 3149 *needBuffer = true; 3150 } 3151 } 3152 } 3153 else 3154 { 3155 if (needBuffer) 3156 { 3157 *needBuffer = false; 3158 } 3159 } 3160 3161 { 3162 static DFTFunc dft_tbl[6] = 3163 { 3164 (DFTFunc)DFT_32f, 3165 (DFTFunc)RealDFT_32f, 3166 (DFTFunc)CCSIDFT_32f, 3167 (DFTFunc)DFT_64f, 3168 (DFTFunc)RealDFT_64f, 3169 (DFTFunc)CCSIDFT_64f 3170 }; 3171 int idx = 0; 3172 if (stage == 0) 3173 { 3174 if (real_transform) 3175 { 3176 if (!opt.isInverse) 3177 idx = 1; 3178 else 3179 idx = 2; 3180 } 3181 } 3182 if (depth == CV_64F) 3183 idx += 3; 3184 3185 opt.dft_func = dft_tbl[idx]; 3186 } 3187 3188 if(!needAnotherStage && (flags & CV_HAL_DFT_SCALE) != 0) 3189 { 3190 int rowCount = count; 3191 if (stage == 0 && (flags & CV_HAL_DFT_ROWS) != 0) 3192 rowCount = 1; 3193 opt.scale = 1./(len * rowCount); 3194 } 3195 } 3196 3197 void apply(const uchar *src, uchar *dst) CV_OVERRIDE 3198 { 3199 opt.dft_func(opt, src, dst); 3200 } 3201 3202 void free() {} 3203 }; 3204 3205 struct ReplacementDFT1D : public hal::DFT1D 3206 { 3207 cvhalDFT *context; 3208 bool isInitialized; 3209 3210 ReplacementDFT1D() : context(0), isInitialized(false) {} 3211 bool init(int len, int count, int depth, int flags, bool *needBuffer) 3212 { 3213 int res = cv_hal_dftInit1D(&context, len, count, depth, flags, needBuffer); 3214 isInitialized = (res == CV_HAL_ERROR_OK); 3215 return isInitialized; 3216 } 3217 void apply(const uchar *src, uchar *dst) CV_OVERRIDE 3218 { 3219 if (isInitialized) 3220 { 3221 CALL_HAL(dft1D, cv_hal_dft1D, context, src, dst); 3222 } 3223 } 3224 ~ReplacementDFT1D() 3225 { 3226 if (isInitialized) 3227 { 3228 CALL_HAL(dftFree1D, cv_hal_dftFree1D, context); 3229 } 3230 } 3231 }; 3232 3233 struct ReplacementDFT2D : public hal::DFT2D 3234 { 3235 cvhalDFT *context; 3236 bool isInitialized; 3237 3238 ReplacementDFT2D() : context(0), isInitialized(false) {} 3239 bool init(int width, int height, int depth, 3240 int src_channels, int dst_channels, 3241 int flags, int nonzero_rows) 3242 { 3243 int res = cv_hal_dftInit2D(&context, width, height, depth, src_channels, dst_channels, flags, nonzero_rows); 3244 isInitialized = (res == CV_HAL_ERROR_OK); 3245 return isInitialized; 3246 } 3247 void apply(const uchar *src, size_t src_step, uchar *dst, size_t dst_step) CV_OVERRIDE 3248 { 3249 if (isInitialized) 3250 { 3251 CALL_HAL(dft2D, cv_hal_dft2D, context, src, src_step, dst, dst_step); 3252 } 3253 } 3254 ~ReplacementDFT2D() 3255 { 3256 if (isInitialized) 3257 { 3258 CALL_HAL(dftFree2D, cv_hal_dftFree1D, context); 3259 } 3260 } 3261 }; 3262 3263 namespace hal { 3264 3265 //================== 1D ====================== 3266 3267 Ptr<DFT1D> DFT1D::create(int len, int count, int depth, int flags, bool *needBuffer) 3268 { 3269 { 3270 ReplacementDFT1D *impl = new ReplacementDFT1D(); 3271 if (impl->init(len, count, depth, flags, needBuffer)) 3272 { 3273 return Ptr<DFT1D>(impl); 3274 } 3275 delete impl; 3276 } 3277 { 3278 OcvDftBasicImpl *impl = new OcvDftBasicImpl(); 3279 impl->init(len, count, depth, flags, needBuffer); 3280 return Ptr<DFT1D>(impl); 3281 } 3282 } 3283 3284 //================== 2D ====================== 3285 3286 Ptr<DFT2D> DFT2D::create(int width, int height, int depth, 3287 int src_channels, int dst_channels, 3288 int flags, int nonzero_rows) 3289 { 3290 { 3291 ReplacementDFT2D *impl = new ReplacementDFT2D(); 3292 if (impl->init(width, height, depth, src_channels, dst_channels, flags, nonzero_rows)) 3293 { 3294 return Ptr<DFT2D>(impl); 3295 } 3296 delete impl; 3297 } 3298 { 3299 if(width == 1 && nonzero_rows > 0 ) 3300 { 3301 CV_Error( CV_StsNotImplemented, 3302 "This mode (using nonzero_rows with a single-column matrix) breaks the function's logic, so it is prohibited.\n" 3303 "For fast convolution/correlation use 2-column matrix or single-row matrix instead" ); 3304 } 3305 OcvDftImpl *impl = new OcvDftImpl(); 3306 impl->init(width, height, depth, src_channels, dst_channels, flags, nonzero_rows); 3307 return Ptr<DFT2D>(impl); 3308 } 3309 } 3310 3311 } // cv::hal:: 3312 } // cv:: 3313 3314 3315 void cv::dft( InputArray _src0, OutputArray _dst, int flags, int nonzero_rows ) 3316 { 3317 CV_INSTRUMENT_REGION(); 3318 3319 #ifdef HAVE_CLAMDFFT 3320 CV_OCL_RUN(ocl::haveAmdFft() && ocl::Device::getDefault().type() != ocl::Device::TYPE_CPU && 3321 _dst.isUMat() && _src0.dims() <= 2 && nonzero_rows == 0, 3322 ocl_dft_amdfft(_src0, _dst, flags)) 3323 #endif 3324 3325 #ifdef HAVE_OPENCL 3326 CV_OCL_RUN(_dst.isUMat() && _src0.dims() <= 2, 3327 ocl_dft(_src0, _dst, flags, nonzero_rows)) 3328 #endif 3329 3330 Mat src0 = _src0.getMat(), src = src0; 3331 bool inv = (flags & DFT_INVERSE) != 0; 3332 int type = src.type(); 3333 int depth = src.depth(); 3334 3335 CV_Assert( type == CV_32FC1 || type == CV_32FC2 || type == CV_64FC1 || type == CV_64FC2 ); 3336 3337 // Fail if DFT_COMPLEX_INPUT is specified, but src is not 2 channels. 3338 CV_Assert( !((flags & DFT_COMPLEX_INPUT) && src.channels() != 2) ); 3339 3340 if( !inv && src.channels() == 1 && (flags & DFT_COMPLEX_OUTPUT) ) 3341 _dst.create( src.size(), CV_MAKETYPE(depth, 2) ); 3342 else if( inv && src.channels() == 2 && (flags & DFT_REAL_OUTPUT) ) 3343 _dst.create( src.size(), depth ); 3344 else 3345 _dst.create( src.size(), type ); 3346 3347 Mat dst = _dst.getMat(); 3348 3349 int f = 0; 3350 if (src.isContinuous() && dst.isContinuous()) 3351 f |= CV_HAL_DFT_IS_CONTINUOUS; 3352 if (inv) 3353 f |= CV_HAL_DFT_INVERSE; 3354 if (flags & DFT_ROWS) 3355 f |= CV_HAL_DFT_ROWS; 3356 if (flags & DFT_SCALE) 3357 f |= CV_HAL_DFT_SCALE; 3358 if (src.data == dst.data) 3359 f |= CV_HAL_DFT_IS_INPLACE; 3360 Ptr<hal::DFT2D> c = hal::DFT2D::create(src.cols, src.rows, depth, src.channels(), dst.channels(), f, nonzero_rows); 3361 c->apply(src.data, src.step, dst.data, dst.step); 3362 } 3363 3364 3365 void cv::idft( InputArray src, OutputArray dst, int flags, int nonzero_rows ) 3366 { 3367 CV_INSTRUMENT_REGION(); 3368 3369 dft( src, dst, flags | DFT_INVERSE, nonzero_rows ); 3370 } 3371 3372 #ifdef HAVE_OPENCL 3373 3374 namespace cv { 3375 3376 static bool ocl_mulSpectrums( InputArray _srcA, InputArray _srcB, 3377 OutputArray _dst, int flags, bool conjB ) 3378 { 3379 int atype = _srcA.type(), btype = _srcB.type(), 3380 rowsPerWI = ocl::Device::getDefault().isIntel() ? 4 : 1; 3381 Size asize = _srcA.size(), bsize = _srcB.size(); 3382 CV_Assert(asize == bsize); 3383 3384 if ( !(atype == CV_32FC2 && btype == CV_32FC2) || flags != 0 ) 3385 return false; 3386 3387 UMat A = _srcA.getUMat(), B = _srcB.getUMat(); 3388 CV_Assert(A.size() == B.size()); 3389 3390 _dst.create(A.size(), atype); 3391 UMat dst = _dst.getUMat(); 3392 3393 ocl::Kernel k("mulAndScaleSpectrums", 3394 ocl::core::mulspectrums_oclsrc, 3395 format("%s", conjB ? "-D CONJ" : "")); 3396 if (k.empty()) 3397 return false; 3398 3399 k.args(ocl::KernelArg::ReadOnlyNoSize(A), ocl::KernelArg::ReadOnlyNoSize(B), 3400 ocl::KernelArg::WriteOnly(dst), rowsPerWI); 3401 3402 size_t globalsize[2] = { (size_t)asize.width, ((size_t)asize.height + rowsPerWI - 1) / rowsPerWI }; 3403 return k.run(2, globalsize, NULL, false); 3404 } 3405 3406 } 3407 3408 #endif 3409 3410 namespace { 3411 3412 #define VAL(buf, elem) (((T*)((char*)data ## buf + (step ## buf * (elem))))[0]) 3413 #define MUL_SPECTRUMS_COL(A, B, C) \ 3414 VAL(C, 0) = VAL(A, 0) * VAL(B, 0); \ 3415 for (size_t j = 1; j <= rows - 2; j += 2) \ 3416 { \ 3417 double a_re = VAL(A, j), a_im = VAL(A, j + 1); \ 3418 double b_re = VAL(B, j), b_im = VAL(B, j + 1); \ 3419 if (conjB) b_im = -b_im; \ 3420 double c_re = a_re * b_re - a_im * b_im; \ 3421 double c_im = a_re * b_im + a_im * b_re; \ 3422 VAL(C, j) = (T)c_re; VAL(C, j + 1) = (T)c_im; \ 3423 } \ 3424 if ((rows & 1) == 0) \ 3425 VAL(C, rows-1) = VAL(A, rows-1) * VAL(B, rows-1) 3426 3427 template <typename T, bool conjB> static inline 3428 void mulSpectrums_processCol_noinplace(const T* dataA, const T* dataB, T* dataC, size_t stepA, size_t stepB, size_t stepC, size_t rows) 3429 { 3430 MUL_SPECTRUMS_COL(A, B, C); 3431 } 3432 3433 template <typename T, bool conjB> static inline 3434 void mulSpectrums_processCol_inplaceA(const T* dataB, T* dataAC, size_t stepB, size_t stepAC, size_t rows) 3435 { 3436 MUL_SPECTRUMS_COL(AC, B, AC); 3437 } 3438 template <typename T, bool conjB, bool inplaceA> static inline 3439 void mulSpectrums_processCol(const T* dataA, const T* dataB, T* dataC, size_t stepA, size_t stepB, size_t stepC, size_t rows) 3440 { 3441 if (inplaceA) 3442 mulSpectrums_processCol_inplaceA<T, conjB>(dataB, dataC, stepB, stepC, rows); 3443 else 3444 mulSpectrums_processCol_noinplace<T, conjB>(dataA, dataB, dataC, stepA, stepB, stepC, rows); 3445 } 3446 #undef MUL_SPECTRUMS_COL 3447 #undef VAL 3448 3449 template <typename T, bool conjB, bool inplaceA> static inline 3450 void mulSpectrums_processCols(const T* dataA, const T* dataB, T* dataC, size_t stepA, size_t stepB, size_t stepC, size_t rows, size_t cols) 3451 { 3452 mulSpectrums_processCol<T, conjB, inplaceA>(dataA, dataB, dataC, stepA, stepB, stepC, rows); 3453 if ((cols & 1) == 0) 3454 { 3455 mulSpectrums_processCol<T, conjB, inplaceA>(dataA + cols - 1, dataB + cols - 1, dataC + cols - 1, stepA, stepB, stepC, rows); 3456 } 3457 } 3458 3459 #define VAL(buf, elem) (data ## buf[(elem)]) 3460 #define MUL_SPECTRUMS_ROW(A, B, C) \ 3461 for (size_t j = j0; j < j1; j += 2) \ 3462 { \ 3463 double a_re = VAL(A, j), a_im = VAL(A, j + 1); \ 3464 double b_re = VAL(B, j), b_im = VAL(B, j + 1); \ 3465 if (conjB) b_im = -b_im; \ 3466 double c_re = a_re * b_re - a_im * b_im; \ 3467 double c_im = a_re * b_im + a_im * b_re; \ 3468 VAL(C, j) = (T)c_re; VAL(C, j + 1) = (T)c_im; \ 3469 } 3470 template <typename T, bool conjB> static inline 3471 void mulSpectrums_processRow_noinplace(const T* dataA, const T* dataB, T* dataC, size_t j0, size_t j1) 3472 { 3473 MUL_SPECTRUMS_ROW(A, B, C); 3474 } 3475 template <typename T, bool conjB> static inline 3476 void mulSpectrums_processRow_inplaceA(const T* dataB, T* dataAC, size_t j0, size_t j1) 3477 { 3478 MUL_SPECTRUMS_ROW(AC, B, AC); 3479 } 3480 template <typename T, bool conjB, bool inplaceA> static inline 3481 void mulSpectrums_processRow(const T* dataA, const T* dataB, T* dataC, size_t j0, size_t j1) 3482 { 3483 if (inplaceA) 3484 mulSpectrums_processRow_inplaceA<T, conjB>(dataB, dataC, j0, j1); 3485 else 3486 mulSpectrums_processRow_noinplace<T, conjB>(dataA, dataB, dataC, j0, j1); 3487 } 3488 #undef MUL_SPECTRUMS_ROW 3489 #undef VAL 3490 3491 template <typename T, bool conjB, bool inplaceA> static inline 3492 void mulSpectrums_processRows(const T* dataA, const T* dataB, T* dataC, size_t stepA, size_t stepB, size_t stepC, size_t rows, size_t cols, size_t j0, size_t j1, bool is_1d_CN1) 3493 { 3494 while (rows-- > 0) 3495 { 3496 if (is_1d_CN1) 3497 dataC[0] = dataA[0]*dataB[0]; 3498 mulSpectrums_processRow<T, conjB, inplaceA>(dataA, dataB, dataC, j0, j1); 3499 if (is_1d_CN1 && (cols & 1) == 0) 3500 dataC[j1] = dataA[j1]*dataB[j1]; 3501 3502 dataA = (const T*)(((char*)dataA) + stepA); 3503 dataB = (const T*)(((char*)dataB) + stepB); 3504 dataC = (T*)(((char*)dataC) + stepC); 3505 } 3506 } 3507 3508 3509 template <typename T, bool conjB, bool inplaceA> static inline 3510 void mulSpectrums_Impl_(const T* dataA, const T* dataB, T* dataC, size_t stepA, size_t stepB, size_t stepC, size_t rows, size_t cols, size_t j0, size_t j1, bool is_1d, bool isCN1) 3511 { 3512 if (!is_1d && isCN1) 3513 { 3514 mulSpectrums_processCols<T, conjB, inplaceA>(dataA, dataB, dataC, stepA, stepB, stepC, rows, cols); 3515 } 3516 mulSpectrums_processRows<T, conjB, inplaceA>(dataA, dataB, dataC, stepA, stepB, stepC, rows, cols, j0, j1, is_1d && isCN1); 3517 } 3518 template <typename T, bool conjB> static inline 3519 void mulSpectrums_Impl(const T* dataA, const T* dataB, T* dataC, size_t stepA, size_t stepB, size_t stepC, size_t rows, size_t cols, size_t j0, size_t j1, bool is_1d, bool isCN1) 3520 { 3521 if (dataA == dataC) 3522 mulSpectrums_Impl_<T, conjB, true>(dataA, dataB, dataC, stepA, stepB, stepC, rows, cols, j0, j1, is_1d, isCN1); 3523 else 3524 mulSpectrums_Impl_<T, conjB, false>(dataA, dataB, dataC, stepA, stepB, stepC, rows, cols, j0, j1, is_1d, isCN1); 3525 } 3526 3527 } // namespace 3528 3529 void cv::mulSpectrums( InputArray _srcA, InputArray _srcB, 3530 OutputArray _dst, int flags, bool conjB ) 3531 { 3532 CV_INSTRUMENT_REGION(); 3533 3534 CV_OCL_RUN(_dst.isUMat() && _srcA.dims() <= 2 && _srcB.dims() <= 2, 3535 ocl_mulSpectrums(_srcA, _srcB, _dst, flags, conjB)) 3536 3537 Mat srcA = _srcA.getMat(), srcB = _srcB.getMat(); 3538 int depth = srcA.depth(), cn = srcA.channels(), type = srcA.type(); 3539 size_t rows = srcA.rows, cols = srcA.cols; 3540 3541 CV_Assert( type == srcB.type() && srcA.size() == srcB.size() ); 3542 CV_Assert( type == CV_32FC1 || type == CV_32FC2 || type == CV_64FC1 || type == CV_64FC2 ); 3543 3544 _dst.create( srcA.rows, srcA.cols, type ); 3545 Mat dst = _dst.getMat(); 3546 3547 // correct inplace support 3548 // Case 'dst.data == srcA.data' is handled by implementation, 3549 // because it is used frequently (filter2D, matchTemplate) 3550 if (dst.data == srcB.data) 3551 srcB = srcB.clone(); // workaround for B only 3552 3553 bool is_1d = (flags & DFT_ROWS) 3554 || (rows == 1) 3555 || (cols == 1 && srcA.isContinuous() && srcB.isContinuous() && dst.isContinuous()); 3556 3557 if( is_1d && !(flags & DFT_ROWS) ) 3558 cols = cols + rows - 1, rows = 1; 3559 3560 bool isCN1 = cn == 1; 3561 size_t j0 = isCN1 ? 1 : 0; 3562 size_t j1 = cols*cn - (((cols & 1) == 0 && cn == 1) ? 1 : 0); 3563 3564 if (depth == CV_32F) 3565 { 3566 const float* dataA = srcA.ptr<float>(); 3567 const float* dataB = srcB.ptr<float>(); 3568 float* dataC = dst.ptr<float>(); 3569 if (!conjB) 3570 mulSpectrums_Impl<float, false>(dataA, dataB, dataC, srcA.step, srcB.step, dst.step, rows, cols, j0, j1, is_1d, isCN1); 3571 else 3572 mulSpectrums_Impl<float, true>(dataA, dataB, dataC, srcA.step, srcB.step, dst.step, rows, cols, j0, j1, is_1d, isCN1); 3573 } 3574 else 3575 { 3576 const double* dataA = srcA.ptr<double>(); 3577 const double* dataB = srcB.ptr<double>(); 3578 double* dataC = dst.ptr<double>(); 3579 if (!conjB) 3580 mulSpectrums_Impl<double, false>(dataA, dataB, dataC, srcA.step, srcB.step, dst.step, rows, cols, j0, j1, is_1d, isCN1); 3581 else 3582 mulSpectrums_Impl<double, true>(dataA, dataB, dataC, srcA.step, srcB.step, dst.step, rows, cols, j0, j1, is_1d, isCN1); 3583 } 3584 } 3585 3586 3587 /****************************************************************************************\ 3588 Discrete Cosine Transform 3589 \****************************************************************************************/ 3590 3591 namespace cv 3592 { 3593 3594 /* DCT is calculated using DFT, as described here: 3595 http://www.ece.utexas.edu/~bevans/courses/ee381k/lectures/09_DCT/lecture9/: 3596 */ 3597 template<typename T> static void 3598 DCT( const OcvDftOptions & c, const T* src, size_t src_step, T* dft_src, T* dft_dst, T* dst, size_t dst_step, 3599 const Complex<T>* dct_wave ) 3600 { 3601 static const T sin_45 = (T)0.70710678118654752440084436210485; 3602 3603 int n = c.n; 3604 int j, n2 = n >> 1; 3605 3606 src_step /= sizeof(src[0]); 3607 dst_step /= sizeof(dst[0]); 3608 T* dst1 = dst + (n-1)*dst_step; 3609 3610 if( n == 1 ) 3611 { 3612 dst[0] = src[0]; 3613 return; 3614 } 3615 3616 for( j = 0; j < n2; j++, src += src_step*2 ) 3617 { 3618 dft_src[j] = src[0]; 3619 dft_src[n-j-1] = src[src_step]; 3620 } 3621 3622 RealDFT(c, dft_src, dft_dst); 3623 src = dft_dst; 3624 3625 dst[0] = (T)(src[0]*dct_wave->re*sin_45); 3626 dst += dst_step; 3627 for( j = 1, dct_wave++; j < n2; j++, dct_wave++, 3628 dst += dst_step, dst1 -= dst_step ) 3629 { 3630 T t0 = dct_wave->re*src[j*2-1] - dct_wave->im*src[j*2]; 3631 T t1 = -dct_wave->im*src[j*2-1] - dct_wave->re*src[j*2]; 3632 dst[0] = t0; 3633 dst1[0] = t1; 3634 } 3635 3636 dst[0] = src[n-1]*dct_wave->re; 3637 } 3638 3639 3640 template<typename T> static void 3641 IDCT( const OcvDftOptions & c, const T* src, size_t src_step, T* dft_src, T* dft_dst, T* dst, size_t dst_step, 3642 const Complex<T>* dct_wave) 3643 { 3644 static const T sin_45 = (T)0.70710678118654752440084436210485; 3645 int n = c.n; 3646 int j, n2 = n >> 1; 3647 3648 src_step /= sizeof(src[0]); 3649 dst_step /= sizeof(dst[0]); 3650 const T* src1 = src + (n-1)*src_step; 3651 3652 if( n == 1 ) 3653 { 3654 dst[0] = src[0]; 3655 return; 3656 } 3657 3658 dft_src[0] = (T)(src[0]*2*dct_wave->re*sin_45); 3659 src += src_step; 3660 for( j = 1, dct_wave++; j < n2; j++, dct_wave++, 3661 src += src_step, src1 -= src_step ) 3662 { 3663 T t0 = dct_wave->re*src[0] - dct_wave->im*src1[0]; 3664 T t1 = -dct_wave->im*src[0] - dct_wave->re*src1[0]; 3665 dft_src[j*2-1] = t0; 3666 dft_src[j*2] = t1; 3667 } 3668 3669 dft_src[n-1] = (T)(src[0]*2*dct_wave->re); 3670 CCSIDFT(c, dft_src, dft_dst); 3671 3672 for( j = 0; j < n2; j++, dst += dst_step*2 ) 3673 { 3674 dst[0] = dft_dst[j]; 3675 dst[dst_step] = dft_dst[n-j-1]; 3676 } 3677 } 3678 3679 3680 static void 3681 DCTInit( int n, int elem_size, void* _wave, int inv ) 3682 { 3683 static const double DctScale[] = 3684 { 3685 0.707106781186547570, 0.500000000000000000, 0.353553390593273790, 3686 0.250000000000000000, 0.176776695296636890, 0.125000000000000000, 3687 0.088388347648318447, 0.062500000000000000, 0.044194173824159223, 3688 0.031250000000000000, 0.022097086912079612, 0.015625000000000000, 3689 0.011048543456039806, 0.007812500000000000, 0.005524271728019903, 3690 0.003906250000000000, 0.002762135864009952, 0.001953125000000000, 3691 0.001381067932004976, 0.000976562500000000, 0.000690533966002488, 3692 0.000488281250000000, 0.000345266983001244, 0.000244140625000000, 3693 0.000172633491500622, 0.000122070312500000, 0.000086316745750311, 3694 0.000061035156250000, 0.000043158372875155, 0.000030517578125000 3695 }; 3696 3697 int i; 3698 Complex<double> w, w1; 3699 double t, scale; 3700 3701 if( n == 1 ) 3702 return; 3703 3704 assert( (n&1) == 0 ); 3705 3706 if( (n & (n - 1)) == 0 ) 3707 { 3708 int m; 3709 for( m = 0; (unsigned)(1 << m) < (unsigned)n; m++ ) 3710 ; 3711 scale = (!inv ? 2 : 1)*DctScale[m]; 3712 w1.re = DFTTab[m+2][0]; 3713 w1.im = -DFTTab[m+2][1]; 3714 } 3715 else 3716 { 3717 t = 1./(2*n); 3718 scale = (!inv ? 2 : 1)*std::sqrt(t); 3719 w1.im = sin(-CV_PI*t); 3720 w1.re = std::sqrt(1. - w1.im*w1.im); 3721 } 3722 n >>= 1; 3723 3724 if( elem_size == sizeof(Complex<double>) ) 3725 { 3726 Complex<double>* wave = (Complex<double>*)_wave; 3727 3728 w.re = scale; 3729 w.im = 0.; 3730 3731 for( i = 0; i <= n; i++ ) 3732 { 3733 wave[i] = w; 3734 t = w.re*w1.re - w.im*w1.im; 3735 w.im = w.re*w1.im + w.im*w1.re; 3736 w.re = t; 3737 } 3738 } 3739 else 3740 { 3741 Complex<float>* wave = (Complex<float>*)_wave; 3742 assert( elem_size == sizeof(Complex<float>) ); 3743 3744 w.re = (float)scale; 3745 w.im = 0.f; 3746 3747 for( i = 0; i <= n; i++ ) 3748 { 3749 wave[i].re = (float)w.re; 3750 wave[i].im = (float)w.im; 3751 t = w.re*w1.re - w.im*w1.im; 3752 w.im = w.re*w1.im + w.im*w1.re; 3753 w.re = t; 3754 } 3755 } 3756 } 3757 3758 3759 typedef void (*DCTFunc)(const OcvDftOptions & c, const void* src, size_t src_step, void* dft_src, 3760 void* dft_dst, void* dst, size_t dst_step, const void* dct_wave); 3761 3762 static void DCT_32f(const OcvDftOptions & c, const float* src, size_t src_step, float* dft_src, float* dft_dst, 3763 float* dst, size_t dst_step, const Complexf* dct_wave) 3764 { 3765 DCT(c, src, src_step, dft_src, dft_dst, dst, dst_step, dct_wave); 3766 } 3767 3768 static void IDCT_32f(const OcvDftOptions & c, const float* src, size_t src_step, float* dft_src, float* dft_dst, 3769 float* dst, size_t dst_step, const Complexf* dct_wave) 3770 { 3771 IDCT(c, src, src_step, dft_src, dft_dst, dst, dst_step, dct_wave); 3772 } 3773 3774 static void DCT_64f(const OcvDftOptions & c, const double* src, size_t src_step, double* dft_src, double* dft_dst, 3775 double* dst, size_t dst_step, const Complexd* dct_wave) 3776 { 3777 DCT(c, src, src_step, dft_src, dft_dst, dst, dst_step, dct_wave); 3778 } 3779 3780 static void IDCT_64f(const OcvDftOptions & c, const double* src, size_t src_step, double* dft_src, double* dft_dst, 3781 double* dst, size_t dst_step, const Complexd* dct_wave) 3782 { 3783 IDCT(c, src, src_step, dft_src, dft_dst, dst, dst_step, dct_wave); 3784 } 3785 3786 } 3787 3788 #ifdef HAVE_IPP 3789 namespace cv 3790 { 3791 3792 #if IPP_VERSION_X100 >= 900 3793 typedef IppStatus (CV_STDCALL * ippiDCTFunc)(const Ipp32f* pSrc, int srcStep, Ipp32f* pDst, int dstStep, const void* pDCTSpec, Ipp8u* pBuffer); 3794 typedef IppStatus (CV_STDCALL * ippiDCTInit)(void* pDCTSpec, IppiSize roiSize, Ipp8u* pMemInit ); 3795 typedef IppStatus (CV_STDCALL * ippiDCTGetSize)(IppiSize roiSize, int* pSizeSpec, int* pSizeInit, int* pSizeBuf); 3796 #elif IPP_VERSION_X100 >= 700 3797 typedef IppStatus (CV_STDCALL * ippiDCTFunc)(const Ipp32f*, int, Ipp32f*, int, const void*, Ipp8u*); 3798 typedef IppStatus (CV_STDCALL * ippiDCTInitAlloc)(void**, IppiSize, IppHintAlgorithm); 3799 typedef IppStatus (CV_STDCALL * ippiDCTFree)(void* pDCTSpec); 3800 typedef IppStatus (CV_STDCALL * ippiDCTGetBufSize)(const void*, int*); 3801 #endif 3802 3803 class DctIPPLoop_Invoker : public ParallelLoopBody 3804 { 3805 public: 3806 DctIPPLoop_Invoker(const uchar * _src, size_t _src_step, uchar * _dst, size_t _dst_step, int _width, bool _inv, bool *_ok) : 3807 ParallelLoopBody(), src(_src), src_step(_src_step), dst(_dst), dst_step(_dst_step), width(_width), inv(_inv), ok(_ok) 3808 { 3809 *ok = true; 3810 } 3811 3812 virtual void operator()(const Range& range) const CV_OVERRIDE 3813 { 3814 if(*ok == false) 3815 return; 3816 3817 #if IPP_VERSION_X100 >= 900 3818 IppiSize srcRoiSize = {width, 1}; 3819 3820 int specSize = 0; 3821 int initSize = 0; 3822 int bufferSize = 0; 3823 3824 Ipp8u* pDCTSpec = NULL; 3825 Ipp8u* pBuffer = NULL; 3826 Ipp8u* pInitBuf = NULL; 3827 3828 #define IPP_RETURN \ 3829 if(pDCTSpec) \ 3830 ippFree(pDCTSpec); \ 3831 if(pBuffer) \ 3832 ippFree(pBuffer); \ 3833 if(pInitBuf) \ 3834 ippFree(pInitBuf); \ 3835 return; 3836 3837 ippiDCTFunc ippiDCT_32f_C1R = inv ? (ippiDCTFunc)ippiDCTInv_32f_C1R : (ippiDCTFunc)ippiDCTFwd_32f_C1R; 3838 ippiDCTInit ippDctInit = inv ? (ippiDCTInit)ippiDCTInvInit_32f : (ippiDCTInit)ippiDCTFwdInit_32f; 3839 ippiDCTGetSize ippDctGetSize = inv ? (ippiDCTGetSize)ippiDCTInvGetSize_32f : (ippiDCTGetSize)ippiDCTFwdGetSize_32f; 3840 3841 if(ippDctGetSize(srcRoiSize, &specSize, &initSize, &bufferSize) < 0) 3842 { 3843 *ok = false; 3844 return; 3845 } 3846 3847 pDCTSpec = (Ipp8u*)CV_IPP_MALLOC(specSize); 3848 if(!pDCTSpec && specSize) 3849 { 3850 *ok = false; 3851 return; 3852 } 3853 3854 pBuffer = (Ipp8u*)CV_IPP_MALLOC(bufferSize); 3855 if(!pBuffer && bufferSize) 3856 { 3857 *ok = false; 3858 IPP_RETURN 3859 } 3860 pInitBuf = (Ipp8u*)CV_IPP_MALLOC(initSize); 3861 if(!pInitBuf && initSize) 3862 { 3863 *ok = false; 3864 IPP_RETURN 3865 } 3866 3867 if(ippDctInit(pDCTSpec, srcRoiSize, pInitBuf) < 0) 3868 { 3869 *ok = false; 3870 IPP_RETURN 3871 } 3872 3873 for(int i = range.start; i < range.end; ++i) 3874 { 3875 if(CV_INSTRUMENT_FUN_IPP(ippiDCT_32f_C1R, (float*)(src + src_step * i), static_cast<int>(src_step), (float*)(dst + dst_step * i), static_cast<int>(dst_step), pDCTSpec, pBuffer) < 0) 3876 { 3877 *ok = false; 3878 IPP_RETURN 3879 } 3880 } 3881 IPP_RETURN 3882 #undef IPP_RETURN 3883 #elif IPP_VERSION_X100 >= 700 3884 void* pDCTSpec; 3885 AutoBuffer<uchar> buf; 3886 uchar* pBuffer = 0; 3887 int bufSize=0; 3888 3889 IppiSize srcRoiSize = {width, 1}; 3890 3891 CV_SUPPRESS_DEPRECATED_START 3892 3893 ippiDCTFunc ippDctFun = inv ? (ippiDCTFunc)ippiDCTInv_32f_C1R : (ippiDCTFunc)ippiDCTFwd_32f_C1R; 3894 ippiDCTInitAlloc ippInitAlloc = inv ? (ippiDCTInitAlloc)ippiDCTInvInitAlloc_32f : (ippiDCTInitAlloc)ippiDCTFwdInitAlloc_32f; 3895 ippiDCTFree ippFree = inv ? (ippiDCTFree)ippiDCTInvFree_32f : (ippiDCTFree)ippiDCTFwdFree_32f; 3896 ippiDCTGetBufSize ippGetBufSize = inv ? (ippiDCTGetBufSize)ippiDCTInvGetBufSize_32f : (ippiDCTGetBufSize)ippiDCTFwdGetBufSize_32f; 3897 3898 if (ippInitAlloc(&pDCTSpec, srcRoiSize, ippAlgHintNone)>=0 && ippGetBufSize(pDCTSpec, &bufSize)>=0) 3899 { 3900 buf.allocate( bufSize ); 3901 pBuffer = (uchar*)buf; 3902 3903 for( int i = range.start; i < range.end; ++i) 3904 { 3905 if(ippDctFun((float*)(src + src_step * i), static_cast<int>(src_step), (float*)(dst + dst_step * i), static_cast<int>(dst_step), pDCTSpec, (Ipp8u*)pBuffer) < 0) 3906 { 3907 *ok = false; 3908 break; 3909 } 3910 } 3911 } 3912 else 3913 *ok = false; 3914 3915 if (pDCTSpec) 3916 ippFree(pDCTSpec); 3917 3918 CV_SUPPRESS_DEPRECATED_END 3919 #else 3920 CV_UNUSED(range); 3921 *ok = false; 3922 #endif 3923 } 3924 3925 private: 3926 const uchar * src; 3927 size_t src_step; 3928 uchar * dst; 3929 size_t dst_step; 3930 int width; 3931 bool inv; 3932 bool *ok; 3933 }; 3934 3935 static bool DctIPPLoop(const uchar * src, size_t src_step, uchar * dst, size_t dst_step, int width, int height, bool inv) 3936 { 3937 bool ok; 3938 parallel_for_(Range(0, height), DctIPPLoop_Invoker(src, src_step, dst, dst_step, width, inv, &ok), height/(double)(1<<4) ); 3939 return ok; 3940 } 3941 3942 static bool ippi_DCT_32f(const uchar * src, size_t src_step, uchar * dst, size_t dst_step, int width, int height, bool inv, bool row) 3943 { 3944 CV_INSTRUMENT_REGION_IPP(); 3945 3946 if(row) 3947 return DctIPPLoop(src, src_step, dst, dst_step, width, height, inv); 3948 else 3949 { 3950 #if IPP_VERSION_X100 >= 900 3951 IppiSize srcRoiSize = {width, height}; 3952 3953 int specSize = 0; 3954 int initSize = 0; 3955 int bufferSize = 0; 3956 3957 Ipp8u* pDCTSpec = NULL; 3958 Ipp8u* pBuffer = NULL; 3959 Ipp8u* pInitBuf = NULL; 3960 3961 #define IPP_RELEASE \ 3962 if(pDCTSpec) \ 3963 ippFree(pDCTSpec); \ 3964 if(pBuffer) \ 3965 ippFree(pBuffer); \ 3966 if(pInitBuf) \ 3967 ippFree(pInitBuf); \ 3968 3969 ippiDCTFunc ippiDCT_32f_C1R = inv ? (ippiDCTFunc)ippiDCTInv_32f_C1R : (ippiDCTFunc)ippiDCTFwd_32f_C1R; 3970 ippiDCTInit ippDctInit = inv ? (ippiDCTInit)ippiDCTInvInit_32f : (ippiDCTInit)ippiDCTFwdInit_32f; 3971 ippiDCTGetSize ippDctGetSize = inv ? (ippiDCTGetSize)ippiDCTInvGetSize_32f : (ippiDCTGetSize)ippiDCTFwdGetSize_32f; 3972 3973 if(ippDctGetSize(srcRoiSize, &specSize, &initSize, &bufferSize) < 0) 3974 return false; 3975 3976 pDCTSpec = (Ipp8u*)CV_IPP_MALLOC(specSize); 3977 if(!pDCTSpec && specSize) 3978 return false; 3979 3980 pBuffer = (Ipp8u*)CV_IPP_MALLOC(bufferSize); 3981 if(!pBuffer && bufferSize) 3982 { 3983 IPP_RELEASE 3984 return false; 3985 } 3986 pInitBuf = (Ipp8u*)CV_IPP_MALLOC(initSize); 3987 if(!pInitBuf && initSize) 3988 { 3989 IPP_RELEASE 3990 return false; 3991 } 3992 3993 if(ippDctInit(pDCTSpec, srcRoiSize, pInitBuf) < 0) 3994 { 3995 IPP_RELEASE 3996 return false; 3997 } 3998 3999 if(CV_INSTRUMENT_FUN_IPP(ippiDCT_32f_C1R, (float*)src, static_cast<int>(src_step), (float*)dst, static_cast<int>(dst_step), pDCTSpec, pBuffer) < 0) 4000 { 4001 IPP_RELEASE 4002 return false; 4003 } 4004 4005 IPP_RELEASE 4006 return true; 4007 #undef IPP_RELEASE 4008 #elif IPP_VERSION_X100 >= 700 4009 IppStatus status; 4010 void* pDCTSpec; 4011 AutoBuffer<uchar> buf; 4012 uchar* pBuffer = 0; 4013 int bufSize=0; 4014 4015 IppiSize srcRoiSize = {width, height}; 4016 4017 CV_SUPPRESS_DEPRECATED_START 4018 4019 ippiDCTFunc ippDctFun = inv ? (ippiDCTFunc)ippiDCTInv_32f_C1R : (ippiDCTFunc)ippiDCTFwd_32f_C1R; 4020 ippiDCTInitAlloc ippInitAlloc = inv ? (ippiDCTInitAlloc)ippiDCTInvInitAlloc_32f : (ippiDCTInitAlloc)ippiDCTFwdInitAlloc_32f; 4021 ippiDCTFree ippFree = inv ? (ippiDCTFree)ippiDCTInvFree_32f : (ippiDCTFree)ippiDCTFwdFree_32f; 4022 ippiDCTGetBufSize ippGetBufSize = inv ? (ippiDCTGetBufSize)ippiDCTInvGetBufSize_32f : (ippiDCTGetBufSize)ippiDCTFwdGetBufSize_32f; 4023 4024 status = ippStsErr; 4025 4026 if (ippInitAlloc(&pDCTSpec, srcRoiSize, ippAlgHintNone)>=0 && ippGetBufSize(pDCTSpec, &bufSize)>=0) 4027 { 4028 buf.allocate( bufSize ); 4029 pBuffer = (uchar*)buf; 4030 4031 status = ippDctFun((float*)src, static_cast<int>(src_step), (float*)dst, static_cast<int>(dst_step), pDCTSpec, (Ipp8u*)pBuffer); 4032 } 4033 4034 if (pDCTSpec) 4035 ippFree(pDCTSpec); 4036 4037 CV_SUPPRESS_DEPRECATED_END 4038 4039 return status >= 0; 4040 #else 4041 CV_UNUSED(src); CV_UNUSED(dst); CV_UNUSED(inv); CV_UNUSED(row); 4042 return false; 4043 #endif 4044 } 4045 } 4046 } 4047 #endif 4048 4049 namespace cv { 4050 4051 class OcvDctImpl CV_FINAL : public hal::DCT2D 4052 { 4053 public: 4054 OcvDftOptions opt; 4055 4056 int _factors[34]; 4057 AutoBuffer<uint> wave_buf; 4058 AutoBuffer<int> itab_buf; 4059 4060 DCTFunc dct_func; 4061 bool isRowTransform; 4062 bool isInverse; 4063 bool isContinuous; 4064 int start_stage; 4065 int end_stage; 4066 int width; 4067 int height; 4068 int depth; 4069 4070 void init(int _width, int _height, int _depth, int flags) 4071 { 4072 width = _width; 4073 height = _height; 4074 depth = _depth; 4075 isInverse = (flags & CV_HAL_DFT_INVERSE) != 0; 4076 isRowTransform = (flags & CV_HAL_DFT_ROWS) != 0; 4077 isContinuous = (flags & CV_HAL_DFT_IS_CONTINUOUS) != 0; 4078 static DCTFunc dct_tbl[4] = 4079 { 4080 (DCTFunc)DCT_32f, 4081 (DCTFunc)IDCT_32f, 4082 (DCTFunc)DCT_64f, 4083 (DCTFunc)IDCT_64f 4084 }; 4085 dct_func = dct_tbl[(int)isInverse + (depth == CV_64F)*2]; 4086 opt.nf = 0; 4087 opt.isComplex = false; 4088 opt.isInverse = false; 4089 opt.noPermute = false; 4090 opt.scale = 1.; 4091 opt.factors = _factors; 4092 4093 if (isRowTransform || height == 1 || (width == 1 && isContinuous)) 4094 { 4095 start_stage = end_stage = 0; 4096 } 4097 else 4098 { 4099 start_stage = (width == 1); 4100 end_stage = 1; 4101 } 4102 } 4103 void apply(const uchar *src, size_t src_step, uchar *dst, size_t dst_step) CV_OVERRIDE 4104 { 4105 CV_IPP_RUN(IPP_VERSION_X100 >= 700 && depth == CV_32F, ippi_DCT_32f(src, src_step, dst, dst_step, width, height, isInverse, isRowTransform)) 4106 4107 AutoBuffer<uchar> dct_wave; 4108 AutoBuffer<uchar> src_buf, dst_buf; 4109 uchar *src_dft_buf = 0, *dst_dft_buf = 0; 4110 int prev_len = 0; 4111 int elem_size = (depth == CV_32F) ? sizeof(float) : sizeof(double); 4112 int complex_elem_size = elem_size*2; 4113 4114 for(int stage = start_stage ; stage <= end_stage; stage++ ) 4115 { 4116 const uchar* sptr = src; 4117 uchar* dptr = dst; 4118 size_t sstep0, sstep1, dstep0, dstep1; 4119 int len, count; 4120 4121 if( stage == 0 ) 4122 { 4123 len = width; 4124 count = height; 4125 if( len == 1 && !isRowTransform ) 4126 { 4127 len = height; 4128 count = 1; 4129 } 4130 sstep0 = src_step; 4131 dstep0 = dst_step; 4132 sstep1 = dstep1 = elem_size; 4133 } 4134 else 4135 { 4136 len = height; 4137 count = width; 4138 sstep1 = src_step; 4139 dstep1 = dst_step; 4140 sstep0 = dstep0 = elem_size; 4141 } 4142 4143 opt.n = len; 4144 opt.tab_size = len; 4145 4146 if( len != prev_len ) 4147 { 4148 if( len > 1 && (len & 1) ) 4149 CV_Error( CV_StsNotImplemented, "Odd-size DCT\'s are not implemented" ); 4150 4151 opt.nf = DFTFactorize( len, opt.factors ); 4152 bool inplace_transform = opt.factors[0] == opt.factors[opt.nf-1]; 4153 4154 wave_buf.allocate(len*complex_elem_size); 4155 opt.wave = wave_buf.data(); 4156 itab_buf.allocate(len); 4157 opt.itab = itab_buf.data(); 4158 DFTInit( len, opt.nf, opt.factors, opt.itab, complex_elem_size, opt.wave, isInverse ); 4159 4160 dct_wave.allocate((len/2 + 1)*complex_elem_size); 4161 src_buf.allocate(len*elem_size); 4162 src_dft_buf = src_buf.data(); 4163 if(!inplace_transform) 4164 { 4165 dst_buf.allocate(len*elem_size); 4166 dst_dft_buf = dst_buf.data(); 4167 } 4168 else 4169 { 4170 dst_dft_buf = src_buf.data(); 4171 } 4172 DCTInit( len, complex_elem_size, dct_wave.data(), isInverse); 4173 prev_len = len; 4174 } 4175 // otherwise reuse the tables calculated on the previous stage 4176 for(unsigned i = 0; i < static_cast<unsigned>(count); i++ ) 4177 { 4178 dct_func( opt, sptr + i*sstep0, sstep1, src_dft_buf, dst_dft_buf, 4179 dptr + i*dstep0, dstep1, dct_wave.data()); 4180 } 4181 src = dst; 4182 src_step = dst_step; 4183 } 4184 } 4185 }; 4186 4187 struct ReplacementDCT2D : public hal::DCT2D 4188 { 4189 cvhalDFT *context; 4190 bool isInitialized; 4191 4192 ReplacementDCT2D() : context(0), isInitialized(false) {} 4193 bool init(int width, int height, int depth, int flags) 4194 { 4195 int res = hal_ni_dctInit2D(&context, width, height, depth, flags); 4196 isInitialized = (res == CV_HAL_ERROR_OK); 4197 return isInitialized; 4198 } 4199 void apply(const uchar *src_data, size_t src_step, uchar *dst_data, size_t dst_step) CV_OVERRIDE 4200 { 4201 if (isInitialized) 4202 { 4203 CALL_HAL(dct2D, cv_hal_dct2D, context, src_data, src_step, dst_data, dst_step); 4204 } 4205 } 4206 ~ReplacementDCT2D() 4207 { 4208 if (isInitialized) 4209 { 4210 CALL_HAL(dctFree2D, cv_hal_dctFree2D, context); 4211 } 4212 } 4213 }; 4214 4215 namespace hal { 4216 4217 Ptr<DCT2D> DCT2D::create(int width, int height, int depth, int flags) 4218 { 4219 { 4220 ReplacementDCT2D *impl = new ReplacementDCT2D(); 4221 if (impl->init(width, height, depth, flags)) 4222 { 4223 return Ptr<DCT2D>(impl); 4224 } 4225 delete impl; 4226 } 4227 { 4228 OcvDctImpl *impl = new OcvDctImpl(); 4229 impl->init(width, height, depth, flags); 4230 return Ptr<DCT2D>(impl); 4231 } 4232 } 4233 4234 } // cv::hal:: 4235 } // cv:: 4236 4237 void cv::dct( InputArray _src0, OutputArray _dst, int flags ) 4238 { 4239 CV_INSTRUMENT_REGION(); 4240 4241 Mat src0 = _src0.getMat(), src = src0; 4242 int type = src.type(), depth = src.depth(); 4243 4244 CV_Assert( type == CV_32FC1 || type == CV_64FC1 ); 4245 _dst.create( src.rows, src.cols, type ); 4246 Mat dst = _dst.getMat(); 4247 4248 int f = 0; 4249 if ((flags & DFT_ROWS) != 0) 4250 f |= CV_HAL_DFT_ROWS; 4251 if ((flags & DCT_INVERSE) != 0) 4252 f |= CV_HAL_DFT_INVERSE; 4253 if (src.isContinuous() && dst.isContinuous()) 4254 f |= CV_HAL_DFT_IS_CONTINUOUS; 4255 4256 Ptr<hal::DCT2D> c = hal::DCT2D::create(src.cols, src.rows, depth, f); 4257 c->apply(src.data, src.step, dst.data, dst.step); 4258 } 4259 4260 4261 void cv::idct( InputArray src, OutputArray dst, int flags ) 4262 { 4263 CV_INSTRUMENT_REGION(); 4264 4265 dct( src, dst, flags | DCT_INVERSE ); 4266 } 4267 4268 namespace cv 4269 { 4270 4271 static const int optimalDFTSizeTab[] = { 4272 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 27, 30, 32, 36, 40, 45, 48, 4273 50, 54, 60, 64, 72, 75, 80, 81, 90, 96, 100, 108, 120, 125, 128, 135, 144, 150, 160, 4274 162, 180, 192, 200, 216, 225, 240, 243, 250, 256, 270, 288, 300, 320, 324, 360, 375, 4275 384, 400, 405, 432, 450, 480, 486, 500, 512, 540, 576, 600, 625, 640, 648, 675, 720, 4276 729, 750, 768, 800, 810, 864, 900, 960, 972, 1000, 1024, 1080, 1125, 1152, 1200, 4277 1215, 1250, 1280, 1296, 1350, 1440, 1458, 1500, 1536, 1600, 1620, 1728, 1800, 1875, 4278 1920, 1944, 2000, 2025, 2048, 2160, 2187, 2250, 2304, 2400, 2430, 2500, 2560, 2592, 4279 2700, 2880, 2916, 3000, 3072, 3125, 3200, 3240, 3375, 3456, 3600, 3645, 3750, 3840, 4280 3888, 4000, 4050, 4096, 4320, 4374, 4500, 4608, 4800, 4860, 5000, 5120, 5184, 5400, 4281 5625, 5760, 5832, 6000, 6075, 6144, 6250, 6400, 6480, 6561, 6750, 6912, 7200, 7290, 4282 7500, 7680, 7776, 8000, 8100, 8192, 8640, 8748, 9000, 9216, 9375, 9600, 9720, 10000, 4283 10125, 10240, 10368, 10800, 10935, 11250, 11520, 11664, 12000, 12150, 12288, 12500, 4284 12800, 12960, 13122, 13500, 13824, 14400, 14580, 15000, 15360, 15552, 15625, 16000, 4285 16200, 16384, 16875, 17280, 17496, 18000, 18225, 18432, 18750, 19200, 19440, 19683, 4286 20000, 20250, 20480, 20736, 21600, 21870, 22500, 23040, 23328, 24000, 24300, 24576, 4287 25000, 25600, 25920, 26244, 27000, 27648, 28125, 28800, 29160, 30000, 30375, 30720, 4288 31104, 31250, 32000, 32400, 32768, 32805, 33750, 34560, 34992, 36000, 36450, 36864, 4289 37500, 38400, 38880, 39366, 40000, 40500, 40960, 41472, 43200, 43740, 45000, 46080, 4290 46656, 46875, 48000, 48600, 49152, 50000, 50625, 51200, 51840, 52488, 54000, 54675, 4291 55296, 56250, 57600, 58320, 59049, 60000, 60750, 61440, 62208, 62500, 64000, 64800, 4292 65536, 65610, 67500, 69120, 69984, 72000, 72900, 73728, 75000, 76800, 77760, 78125, 4293 78732, 80000, 81000, 81920, 82944, 84375, 86400, 87480, 90000, 91125, 92160, 93312, 4294 93750, 96000, 97200, 98304, 98415, 100000, 101250, 102400, 103680, 104976, 108000, 4295 109350, 110592, 112500, 115200, 116640, 118098, 120000, 121500, 122880, 124416, 125000, 4296 128000, 129600, 131072, 131220, 135000, 138240, 139968, 140625, 144000, 145800, 147456, 4297 150000, 151875, 153600, 155520, 156250, 157464, 160000, 162000, 163840, 164025, 165888, 4298 168750, 172800, 174960, 177147, 180000, 182250, 184320, 186624, 187500, 192000, 194400, 4299 196608, 196830, 200000, 202500, 204800, 207360, 209952, 216000, 218700, 221184, 225000, 4300 230400, 233280, 234375, 236196, 240000, 243000, 245760, 248832, 250000, 253125, 256000, 4301 259200, 262144, 262440, 270000, 273375, 276480, 279936, 281250, 288000, 291600, 294912, 4302 295245, 300000, 303750, 307200, 311040, 312500, 314928, 320000, 324000, 327680, 328050, 4303 331776, 337500, 345600, 349920, 354294, 360000, 364500, 368640, 373248, 375000, 384000, 4304 388800, 390625, 393216, 393660, 400000, 405000, 409600, 414720, 419904, 421875, 432000, 4305 437400, 442368, 450000, 455625, 460800, 466560, 468750, 472392, 480000, 486000, 491520, 4306 492075, 497664, 500000, 506250, 512000, 518400, 524288, 524880, 531441, 540000, 546750, 4307 552960, 559872, 562500, 576000, 583200, 589824, 590490, 600000, 607500, 614400, 622080, 4308 625000, 629856, 640000, 648000, 655360, 656100, 663552, 675000, 691200, 699840, 703125, 4309 708588, 720000, 729000, 737280, 746496, 750000, 759375, 768000, 777600, 781250, 786432, 4310 787320, 800000, 810000, 819200, 820125, 829440, 839808, 843750, 864000, 874800, 884736, 4311 885735, 900000, 911250, 921600, 933120, 937500, 944784, 960000, 972000, 983040, 984150, 4312 995328, 1000000, 1012500, 1024000, 1036800, 1048576, 1049760, 1062882, 1080000, 1093500, 4313 1105920, 1119744, 1125000, 1152000, 1166400, 1171875, 1179648, 1180980, 1200000, 4314 1215000, 1228800, 1244160, 1250000, 1259712, 1265625, 1280000, 1296000, 1310720, 4315 1312200, 1327104, 1350000, 1366875, 1382400, 1399680, 1406250, 1417176, 1440000, 4316 1458000, 1474560, 1476225, 1492992, 1500000, 1518750, 1536000, 1555200, 1562500, 4317 1572864, 1574640, 1594323, 1600000, 1620000, 1638400, 1640250, 1658880, 1679616, 4318 1687500, 1728000, 1749600, 1769472, 1771470, 1800000, 1822500, 1843200, 1866240, 4319 1875000, 1889568, 1920000, 1944000, 1953125, 1966080, 1968300, 1990656, 2000000, 4320 2025000, 2048000, 2073600, 2097152, 2099520, 2109375, 2125764, 2160000, 2187000, 4321 2211840, 2239488, 2250000, 2278125, 2304000, 2332800, 2343750, 2359296, 2361960, 4322 2400000, 2430000, 2457600, 2460375, 2488320, 2500000, 2519424, 2531250, 2560000, 4323 2592000, 2621440, 2624400, 2654208, 2657205, 2700000, 2733750, 2764800, 2799360, 4324 2812500, 2834352, 2880000, 2916000, 2949120, 2952450, 2985984, 3000000, 3037500, 4325 3072000, 3110400, 3125000, 3145728, 3149280, 3188646, 3200000, 3240000, 3276800, 4326 3280500, 3317760, 3359232, 3375000, 3456000, 3499200, 3515625, 3538944, 3542940, 4327 3600000, 3645000, 3686400, 3732480, 3750000, 3779136, 3796875, 3840000, 3888000, 4328 3906250, 3932160, 3936600, 3981312, 4000000, 4050000, 4096000, 4100625, 4147200, 4329 4194304, 4199040, 4218750, 4251528, 4320000, 4374000, 4423680, 4428675, 4478976, 4330 4500000, 4556250, 4608000, 4665600, 4687500, 4718592, 4723920, 4782969, 4800000, 4331 4860000, 4915200, 4920750, 4976640, 5000000, 5038848, 5062500, 5120000, 5184000, 4332 5242880, 5248800, 5308416, 5314410, 5400000, 5467500, 5529600, 5598720, 5625000, 4333 5668704, 5760000, 5832000, 5859375, 5898240, 5904900, 5971968, 6000000, 6075000, 4334 6144000, 6220800, 6250000, 6291456, 6298560, 6328125, 6377292, 6400000, 6480000, 4335 6553600, 6561000, 6635520, 6718464, 6750000, 6834375, 6912000, 6998400, 7031250, 4336 7077888, 7085880, 7200000, 7290000, 7372800, 7381125, 7464960, 7500000, 7558272, 4337 7593750, 7680000, 7776000, 7812500, 7864320, 7873200, 7962624, 7971615, 8000000, 4338 8100000, 8192000, 8201250, 8294400, 8388608, 8398080, 8437500, 8503056, 8640000, 4339 8748000, 8847360, 8857350, 8957952, 9000000, 9112500, 9216000, 9331200, 9375000, 4340 9437184, 9447840, 9565938, 9600000, 9720000, 9765625, 9830400, 9841500, 9953280, 4341 10000000, 10077696, 10125000, 10240000, 10368000, 10485760, 10497600, 10546875, 10616832, 4342 10628820, 10800000, 10935000, 11059200, 11197440, 11250000, 11337408, 11390625, 11520000, 4343 11664000, 11718750, 11796480, 11809800, 11943936, 12000000, 12150000, 12288000, 12301875, 4344 12441600, 12500000, 12582912, 12597120, 12656250, 12754584, 12800000, 12960000, 13107200, 4345 13122000, 13271040, 13286025, 13436928, 13500000, 13668750, 13824000, 13996800, 14062500, 4346 14155776, 14171760, 14400000, 14580000, 14745600, 14762250, 14929920, 15000000, 15116544, 4347 15187500, 15360000, 15552000, 15625000, 15728640, 15746400, 15925248, 15943230, 16000000, 4348 16200000, 16384000, 16402500, 16588800, 16777216, 16796160, 16875000, 17006112, 17280000, 4349 17496000, 17578125, 17694720, 17714700, 17915904, 18000000, 18225000, 18432000, 18662400, 4350 18750000, 18874368, 18895680, 18984375, 19131876, 19200000, 19440000, 19531250, 19660800, 4351 19683000, 19906560, 20000000, 20155392, 20250000, 20480000, 20503125, 20736000, 20971520, 4352 20995200, 21093750, 21233664, 21257640, 21600000, 21870000, 22118400, 22143375, 22394880, 4353 22500000, 22674816, 22781250, 23040000, 23328000, 23437500, 23592960, 23619600, 23887872, 4354 23914845, 24000000, 24300000, 24576000, 24603750, 24883200, 25000000, 25165824, 25194240, 4355 25312500, 25509168, 25600000, 25920000, 26214400, 26244000, 26542080, 26572050, 26873856, 4356 27000000, 27337500, 27648000, 27993600, 28125000, 28311552, 28343520, 28800000, 29160000, 4357 29296875, 29491200, 29524500, 29859840, 30000000, 30233088, 30375000, 30720000, 31104000, 4358 31250000, 31457280, 31492800, 31640625, 31850496, 31886460, 32000000, 32400000, 32768000, 4359 32805000, 33177600, 33554432, 33592320, 33750000, 34012224, 34171875, 34560000, 34992000, 4360 35156250, 35389440, 35429400, 35831808, 36000000, 36450000, 36864000, 36905625, 37324800, 4361 37500000, 37748736, 37791360, 37968750, 38263752, 38400000, 38880000, 39062500, 39321600, 4362 39366000, 39813120, 39858075, 40000000, 40310784, 40500000, 40960000, 41006250, 41472000, 4363 41943040, 41990400, 42187500, 42467328, 42515280, 43200000, 43740000, 44236800, 44286750, 4364 44789760, 45000000, 45349632, 45562500, 46080000, 46656000, 46875000, 47185920, 47239200, 4365 47775744, 47829690, 48000000, 48600000, 48828125, 49152000, 49207500, 49766400, 50000000, 4366 50331648, 50388480, 50625000, 51018336, 51200000, 51840000, 52428800, 52488000, 52734375, 4367 53084160, 53144100, 53747712, 54000000, 54675000, 55296000, 55987200, 56250000, 56623104, 4368 56687040, 56953125, 57600000, 58320000, 58593750, 58982400, 59049000, 59719680, 60000000, 4369 60466176, 60750000, 61440000, 61509375, 62208000, 62500000, 62914560, 62985600, 63281250, 4370 63700992, 63772920, 64000000, 64800000, 65536000, 65610000, 66355200, 66430125, 67108864, 4371 67184640, 67500000, 68024448, 68343750, 69120000, 69984000, 70312500, 70778880, 70858800, 4372 71663616, 72000000, 72900000, 73728000, 73811250, 74649600, 75000000, 75497472, 75582720, 4373 75937500, 76527504, 76800000, 77760000, 78125000, 78643200, 78732000, 79626240, 79716150, 4374 80000000, 80621568, 81000000, 81920000, 82012500, 82944000, 83886080, 83980800, 84375000, 4375 84934656, 85030560, 86400000, 87480000, 87890625, 88473600, 88573500, 89579520, 90000000, 4376 90699264, 91125000, 92160000, 93312000, 93750000, 94371840, 94478400, 94921875, 95551488, 4377 95659380, 96000000, 97200000, 97656250, 98304000, 98415000, 99532800, 100000000, 4378 100663296, 100776960, 101250000, 102036672, 102400000, 102515625, 103680000, 104857600, 4379 104976000, 105468750, 106168320, 106288200, 107495424, 108000000, 109350000, 110592000, 4380 110716875, 111974400, 112500000, 113246208, 113374080, 113906250, 115200000, 116640000, 4381 117187500, 117964800, 118098000, 119439360, 119574225, 120000000, 120932352, 121500000, 4382 122880000, 123018750, 124416000, 125000000, 125829120, 125971200, 126562500, 127401984, 4383 127545840, 128000000, 129600000, 131072000, 131220000, 132710400, 132860250, 134217728, 4384 134369280, 135000000, 136048896, 136687500, 138240000, 139968000, 140625000, 141557760, 4385 141717600, 143327232, 144000000, 145800000, 146484375, 147456000, 147622500, 149299200, 4386 150000000, 150994944, 151165440, 151875000, 153055008, 153600000, 155520000, 156250000, 4387 157286400, 157464000, 158203125, 159252480, 159432300, 160000000, 161243136, 162000000, 4388 163840000, 164025000, 165888000, 167772160, 167961600, 168750000, 169869312, 170061120, 4389 170859375, 172800000, 174960000, 175781250, 176947200, 177147000, 179159040, 180000000, 4390 181398528, 182250000, 184320000, 184528125, 186624000, 187500000, 188743680, 188956800, 4391 189843750, 191102976, 191318760, 192000000, 194400000, 195312500, 196608000, 196830000, 4392 199065600, 199290375, 200000000, 201326592, 201553920, 202500000, 204073344, 204800000, 4393 205031250, 207360000, 209715200, 209952000, 210937500, 212336640, 212576400, 214990848, 4394 216000000, 218700000, 221184000, 221433750, 223948800, 225000000, 226492416, 226748160, 4395 227812500, 230400000, 233280000, 234375000, 235929600, 236196000, 238878720, 239148450, 4396 240000000, 241864704, 243000000, 244140625, 245760000, 246037500, 248832000, 250000000, 4397 251658240, 251942400, 253125000, 254803968, 255091680, 256000000, 259200000, 262144000, 4398 262440000, 263671875, 265420800, 265720500, 268435456, 268738560, 270000000, 272097792, 4399 273375000, 276480000, 279936000, 281250000, 283115520, 283435200, 284765625, 286654464, 4400 288000000, 291600000, 292968750, 294912000, 295245000, 298598400, 300000000, 301989888, 4401 302330880, 303750000, 306110016, 307200000, 307546875, 311040000, 312500000, 314572800, 4402 314928000, 316406250, 318504960, 318864600, 320000000, 322486272, 324000000, 327680000, 4403 328050000, 331776000, 332150625, 335544320, 335923200, 337500000, 339738624, 340122240, 4404 341718750, 345600000, 349920000, 351562500, 353894400, 354294000, 358318080, 360000000, 4405 362797056, 364500000, 368640000, 369056250, 373248000, 375000000, 377487360, 377913600, 4406 379687500, 382205952, 382637520, 384000000, 388800000, 390625000, 393216000, 393660000, 4407 398131200, 398580750, 400000000, 402653184, 403107840, 405000000, 408146688, 409600000, 4408 410062500, 414720000, 419430400, 419904000, 421875000, 424673280, 425152800, 429981696, 4409 432000000, 437400000, 439453125, 442368000, 442867500, 447897600, 450000000, 452984832, 4410 453496320, 455625000, 460800000, 466560000, 468750000, 471859200, 472392000, 474609375, 4411 477757440, 478296900, 480000000, 483729408, 486000000, 488281250, 491520000, 492075000, 4412 497664000, 500000000, 503316480, 503884800, 506250000, 509607936, 510183360, 512000000, 4413 512578125, 518400000, 524288000, 524880000, 527343750, 530841600, 531441000, 536870912, 4414 537477120, 540000000, 544195584, 546750000, 552960000, 553584375, 559872000, 562500000, 4415 566231040, 566870400, 569531250, 573308928, 576000000, 583200000, 585937500, 589824000, 4416 590490000, 597196800, 597871125, 600000000, 603979776, 604661760, 607500000, 612220032, 4417 614400000, 615093750, 622080000, 625000000, 629145600, 629856000, 632812500, 637009920, 4418 637729200, 640000000, 644972544, 648000000, 655360000, 656100000, 663552000, 664301250, 4419 671088640, 671846400, 675000000, 679477248, 680244480, 683437500, 691200000, 699840000, 4420 703125000, 707788800, 708588000, 716636160, 720000000, 725594112, 729000000, 732421875, 4421 737280000, 738112500, 746496000, 750000000, 754974720, 755827200, 759375000, 764411904, 4422 765275040, 768000000, 777600000, 781250000, 786432000, 787320000, 791015625, 796262400, 4423 797161500, 800000000, 805306368, 806215680, 810000000, 816293376, 819200000, 820125000, 4424 829440000, 838860800, 839808000, 843750000, 849346560, 850305600, 854296875, 859963392, 4425 864000000, 874800000, 878906250, 884736000, 885735000, 895795200, 900000000, 905969664, 4426 906992640, 911250000, 921600000, 922640625, 933120000, 937500000, 943718400, 944784000, 4427 949218750, 955514880, 956593800, 960000000, 967458816, 972000000, 976562500, 983040000, 4428 984150000, 995328000, 996451875, 1000000000, 1006632960, 1007769600, 1012500000, 4429 1019215872, 1020366720, 1024000000, 1025156250, 1036800000, 1048576000, 1049760000, 4430 1054687500, 1061683200, 1062882000, 1073741824, 1074954240, 1080000000, 1088391168, 4431 1093500000, 1105920000, 1107168750, 1119744000, 1125000000, 1132462080, 1133740800, 4432 1139062500, 1146617856, 1152000000, 1166400000, 1171875000, 1179648000, 1180980000, 4433 1194393600, 1195742250, 1200000000, 1207959552, 1209323520, 1215000000, 1220703125, 4434 1224440064, 1228800000, 1230187500, 1244160000, 1250000000, 1258291200, 1259712000, 4435 1265625000, 1274019840, 1275458400, 1280000000, 1289945088, 1296000000, 1310720000, 4436 1312200000, 1318359375, 1327104000, 1328602500, 1342177280, 1343692800, 1350000000, 4437 1358954496, 1360488960, 1366875000, 1382400000, 1399680000, 1406250000, 1415577600, 4438 1417176000, 1423828125, 1433272320, 1440000000, 1451188224, 1458000000, 1464843750, 4439 1474560000, 1476225000, 1492992000, 1500000000, 1509949440, 1511654400, 1518750000, 4440 1528823808, 1530550080, 1536000000, 1537734375, 1555200000, 1562500000, 1572864000, 4441 1574640000, 1582031250, 1592524800, 1594323000, 1600000000, 1610612736, 1612431360, 4442 1620000000, 1632586752, 1638400000, 1640250000, 1658880000, 1660753125, 1677721600, 4443 1679616000, 1687500000, 1698693120, 1700611200, 1708593750, 1719926784, 1728000000, 4444 1749600000, 1757812500, 1769472000, 1771470000, 1791590400, 1800000000, 1811939328, 4445 1813985280, 1822500000, 1843200000, 1845281250, 1866240000, 1875000000, 1887436800, 4446 1889568000, 1898437500, 1911029760, 1913187600, 1920000000, 1934917632, 1944000000, 4447 1953125000, 1966080000, 1968300000, 1990656000, 1992903750, 2000000000, 2013265920, 4448 2015539200, 2025000000, 2038431744, 2040733440, 2048000000, 2050312500, 2073600000, 4449 2097152000, 2099520000, 2109375000, 2123366400, 2125764000 4450 }; 4451 4452 } 4453 4454 int cv::getOptimalDFTSize( int size0 ) 4455 { 4456 int a = 0, b = sizeof(optimalDFTSizeTab)/sizeof(optimalDFTSizeTab[0]) - 1; 4457 if( (unsigned)size0 >= (unsigned)optimalDFTSizeTab[b] ) 4458 return -1; 4459 4460 while( a < b ) 4461 { 4462 int c = (a + b) >> 1; 4463 if( size0 <= optimalDFTSizeTab[c] ) 4464 b = c; 4465 else 4466 a = c+1; 4467 } 4468 4469 return optimalDFTSizeTab[b]; 4470 } 4471 4472 CV_IMPL void 4473 cvDFT( const CvArr* srcarr, CvArr* dstarr, int flags, int nonzero_rows ) 4474 { 4475 cv::Mat src = cv::cvarrToMat(srcarr), dst0 = cv::cvarrToMat(dstarr), dst = dst0; 4476 int _flags = ((flags & CV_DXT_INVERSE) ? cv::DFT_INVERSE : 0) | 4477 ((flags & CV_DXT_SCALE) ? cv::DFT_SCALE : 0) | 4478 ((flags & CV_DXT_ROWS) ? cv::DFT_ROWS : 0); 4479 4480 CV_Assert( src.size == dst.size ); 4481 4482 if( src.type() != dst.type() ) 4483 { 4484 if( dst.channels() == 2 ) 4485 _flags |= cv::DFT_COMPLEX_OUTPUT; 4486 else 4487 _flags |= cv::DFT_REAL_OUTPUT; 4488 } 4489 4490 cv::dft( src, dst, _flags, nonzero_rows ); 4491 CV_Assert( dst.data == dst0.data ); // otherwise it means that the destination size or type was incorrect 4492 } 4493 4494 4495 CV_IMPL void 4496 cvMulSpectrums( const CvArr* srcAarr, const CvArr* srcBarr, 4497 CvArr* dstarr, int flags ) 4498 { 4499 cv::Mat srcA = cv::cvarrToMat(srcAarr), 4500 srcB = cv::cvarrToMat(srcBarr), 4501 dst = cv::cvarrToMat(dstarr); 4502 CV_Assert( srcA.size == dst.size && srcA.type() == dst.type() ); 4503 4504 cv::mulSpectrums(srcA, srcB, dst, 4505 (flags & CV_DXT_ROWS) ? cv::DFT_ROWS : 0, 4506 (flags & CV_DXT_MUL_CONJ) != 0 ); 4507 } 4508 4509 4510 CV_IMPL void 4511 cvDCT( const CvArr* srcarr, CvArr* dstarr, int flags ) 4512 { 4513 cv::Mat src = cv::cvarrToMat(srcarr), dst = cv::cvarrToMat(dstarr); 4514 CV_Assert( src.size == dst.size && src.type() == dst.type() ); 4515 int _flags = ((flags & CV_DXT_INVERSE) ? cv::DCT_INVERSE : 0) | 4516 ((flags & CV_DXT_ROWS) ? cv::DCT_ROWS : 0); 4517 cv::dct( src, dst, _flags ); 4518 } 4519 4520 4521 CV_IMPL int 4522 cvGetOptimalDFTSize( int size0 ) 4523 { 4524 return cv::getOptimalDFTSize(size0); 4525 } 4526 4527 /* End of file. */
既然修改源码不是好方法，那么只能靠我们自己了！大约有两个方向：一是在OpenCV的基础上自己写一个傅里叶相关的函数（使傅里叶函数变成一个系数卷积核），该函数理应配合像素遍历、扩充图像边界（以便于卷积）、计算幅值、通道分离、通道混合这些函数同时使用。二是在C/C++与windows系统函数的基础上写相关的函数（其工程量很大，几乎等于从图像的存储结构开始搭建图像处理的所需框架）。那么，除此之外还有什么更好的方法吗？据说，可以使用MFC或QT来实现图像处理。然而，这些工作都是比较耗时的，不利于大家学习“图像处理与分析”的核心思想。不可否认，上述提到的方法是有益于大家的编程能力的提升，因此综合各方面考虑之下。博主本篇文章中编写的代码，只注重性质的侧面演示，不注重傅里叶函数的代码实现。关于这些函数的代码实现，博主将会另开一个系列的随笔较为详细的介绍。
【1】傅里叶变换频谱：使用 dft() 及其相关函数，展示频谱。在实验过程中发现，可以使用二值化的方法使频谱的特性凸显出来。代码如下：
1 #pragma once 2 #include "opencv2/core.hpp" 3 #include "opencv2/imgproc.hpp" 4 #include "opencv2/imgcodecs.hpp" 5 #include "opencv2/highgui.hpp" 6 #include <iostream> 7 using namespace cv; 8 #define GRAY_THRESH 10 9 void binar(Mat magImg) 10 { 11 threshold(magImg, magImg, GRAY_THRESH, 255, THRESH_BINARY); 12 imshow("spectrumedd magnitude", magImg); 13 } 14 15 void translation(Mat magI, Mat I, Mat complexI) 16 { 17 normalize(magI, magI, 0, 1, NORM_MINMAX); // Transform the matrix with float values into a 18 // viewable image form (float between values 0 and 1). 19 imshow("spectrumed magnitude", magI); 20 21 // crop the spectrum, if it has an odd number of rows or columns 22 magI = magI(Rect(0, 0, magI.cols & -2, magI.rows & -2)); 23 // rearrange the quadrants of Fourier image so that the origin is at the image center 24 int cx = magI.cols / 2; 25 int cy = magI.rows / 2; 26 Mat q0(magI, Rect(0, 0, cx, cy)); // Top-Left - Create a ROI per quadrant 27 Mat q1(magI, Rect(cx, 0, cx, cy)); // Top-Right 28 Mat q2(magI, Rect(0, cy, cx, cy)); // Bottom-Left 29 Mat q3(magI, Rect(cx, cy, cx, cy)); // Bottom-Right 30 Mat tmp; // swap quadrants (Top-Left with Bottom-Right) 31 q0.copyTo(tmp); 32 q3.copyTo(q0); 33 tmp.copyTo(q3); 34 q1.copyTo(tmp); // swap quadrant (Top-Right with Bottom-Left) 35 q2.copyTo(q1); 36 tmp.copyTo(q2); 37 38 imshow("Input Image", I); // Show the result 39 imshow("spectrum magnitude", magI); 40 41 // 使用IFFT进行反变换，得到时域图像 42 Mat ifft; 43 idft(complexI, ifft, DFT_REAL_OUTPUT | DFT_SCALE); 44 normalize(ifft, ifft, 0, 1, NORM_MINMAX); 45 imshow("idft", ifft); 46 }
1 #include "Binarization.h" 2 #include <iostream> 3 4 using namespace std; 5 6 static void help(char** argv) 7 { 8 cout << endl 9 << "This program demonstrated the use of the discrete Fourier transform (DFT). " << endl 10 << "The dft of an image is taken and it's power spectrum is displayed." << endl << endl 11 << "Usage:" << endl 12 << argv[0] << " [image_name -- default lena.jpg]" << endl << endl; 13 } 14 int main(int argc, char** argv) 15 { 16 help(argv); 17 const char* filename = argc >= 2 ? argv[1] : "1.png"; 18 Mat I = imread(samples::findFile(filename), IMREAD_GRAYSCALE); 19 if (I.empty()) { 20 cout << "Error opening image" << endl; 21 return EXIT_FAILURE; 22 } 23 Mat padded; //expand input image to optimal size 24 int m = getOptimalDFTSize(I.rows); 25 int n = getOptimalDFTSize(I.cols); // on the border add zero values 26 copyMakeBorder(I, padded, 0, m - I.rows, 0, n - I.cols, BORDER_CONSTANT, Scalar::all(0)); 27 Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F) }; 28 Mat complexI; 29 merge(planes, 2, complexI); // Add to the expanded another plane with zeros 30 dft(complexI, complexI); // this way the result may fit in the source matrix 31 // compute the magnitude and switch to logarithmic scale 32 // => log(1 + sqrt(Re(DFT(I))^2 + Im(DFT(I))^2)) 33 split(complexI, planes); // planes[0] = Re(DFT(I), planes[1] = Im(DFT(I)) 34 magnitude(planes[0], planes[1], planes[0]);// planes[0] = magnitude 35 Mat magI = planes[0]; 36 37 // 进行对数尺度缩放 38 magI += Scalar::all(1); // switch to logarithmic scale 39 log(magI, magI); 40 41 Mat bimg=magI.clone(); // 深拷贝，修改新对象，旧对象不变 42 43 normalize(magI, magI, 0, 1, NORM_MINMAX); // Transform the matrix with float values into a 44 // viewable image form (float between values 0 and 1) 45 imshow("spectrumed magnitude", magI); 46 //转为二值图像 47 binar(bimg); 48 49 // translation(magI, I, complexI); 50 51 waitKey(); 52 destroyAllWindows(); 53 return EXIT_SUCCESS; 54 }
运行示例：（注：二值化部分，博主为了频谱图特征凸显出来，使用的像素灰度阈值是10。）
这样，可以清晰地看见图像的大部分信息都集中在四个角。原因是：对于一幅图像，图像中灰度变化比较缓慢的区域可以用较低频率的正弦信号近似，而灰度变化比较大的边缘地带则需要用高频正弦信号近似。一副图像中大部分都是灰度变化缓慢的区域，只有小部分是边缘，因此，其变换域的图像，能量主要集中在低频部分（对应幅值较高），只有小部分能量集中在高频部分（对应的幅值较低）。
【2】平移性：代码如下。
1 #pragma once 2 #include "opencv2/core.hpp" 3 #include "opencv2/imgproc.hpp" 4 #include "opencv2/imgcodecs.hpp" 5 #include "opencv2/highgui.hpp" 6 #include <iostream> 7 using namespace cv; 8 using namespace std; 9 #define GRAY_THRESH 10 10 11 void help(char* argv) 12 { 13 cout << endl 14 << "This program demonstrated the use of the discrete Fourier transform (DFT). " << endl 15 << "The dft of an image is taken and it's power spectrum is displayed." << endl << endl 16 << "Usage:" << endl 17 << argv[0] << " [image_name -- default lena.jpg]" << endl << endl; 18 } 19 20 Mat Predft(Mat I, Mat complexI) 21 { 22 Mat padded; //expand input image to optimal size 23 int m = getOptimalDFTSize(I.rows); 24 int n = getOptimalDFTSize(I.cols); // on the border add zero values 25 copyMakeBorder(I, padded, 0, m - I.rows, 0, n - I.cols, BORDER_CONSTANT, Scalar::all(0)); 26 Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F) }; 27 28 merge(planes, 2, complexI); // Add to the expanded another plane with zeros 29 dft(complexI, complexI); // this way the result may fit in the source matrix 30 // compute the magnitude and switch to logarithmic scale 31 // => log(1 + sqrt(Re(DFT(I))^2 + Im(DFT(I))^2)) 32 split(complexI, planes); // planes[0] = Re(DFT(I), planes[1] = Im(DFT(I)) 33 magnitude(planes[0], planes[1], planes[0]);// planes[0] = magnitude 34 Mat magI = planes[0]; 35 36 // 进行对数尺度缩放 37 magI += Scalar::all(1); // switch to logarithmic scale 38 log(magI, magI); 39 return magI; 40 } 41 42 void binar(Mat magImg) 43 { 44 threshold(magImg, magImg, GRAY_THRESH, 255, THRESH_BINARY); 45 imshow("spectrumedd magnitude", magImg); 46 } 47 48 void translation(Mat magI, Mat I, Mat complexI) 49 { 50 normalize(magI, magI, 0, 1, NORM_MINMAX); // Transform the matrix with float values into a 51 // viewable image form (float between values 0 and 1). 52 // imshow("spectrumed magnitude", magI); 53 54 // crop the spectrum, if it has an odd number of rows or columns 55 magI = magI(Rect(0, 0, magI.cols & -2, magI.rows & -2)); 56 // rearrange the quadrants of Fourier image so that the origin is at the image center 57 int cx = magI.cols / 2; 58 int cy = magI.rows / 2; 59 Mat q0(magI, Rect(0, 0, cx, cy)); // Top-Left - Create a ROI per quadrant 60 Mat q1(magI, Rect(cx, 0, cx, cy)); // Top-Right 61 Mat q2(magI, Rect(0, cy, cx, cy)); // Bottom-Left 62 Mat q3(magI, Rect(cx, cy, cx, cy)); // Bottom-Right 63 Mat tmp; // swap quadrants (Top-Left with Bottom-Right) 64 q0.copyTo(tmp); 65 q3.copyTo(q0); 66 tmp.copyTo(q3); 67 q1.copyTo(tmp); // swap quadrant (Top-Right with Bottom-Left) 68 q2.copyTo(q1); 69 tmp.copyTo(q2); 70 71 //imshow("Input Image", I); // Show the result 72 //imshow("spectrum magnitude", magI); 73 } 74 75 void idft(Mat complexI) 76 { 77 // 使用IFFT进行反变换，得到时域图像 78 Mat ifft; 79 idft(complexI, ifft, DFT_REAL_OUTPUT | DFT_SCALE); 80 normalize(ifft, ifft, 0, 1, NORM_MINMAX); 81 imshow("idft", ifft); 82 }
1 #include "Binarization.h" 2 #include <iostream> 3 4 using namespace std; 5 6 int main(int argc, char** argv) 7 { 8 char fn[] = "1.png"; 9 char fn1[] = "8.png"; 10 help(fn); 11 help(fn1); 12 Mat complexI; 13 Mat complexI1; 14 15 Mat I = imread(samples::findFile(fn), IMREAD_GRAYSCALE); 16 Mat I1 = imread(samples::findFile(fn1), IMREAD_GRAYSCALE); 17 18 if (I.empty() && I1.empty()) { 19 cout << "Error opening image" << endl; 20 return EXIT_FAILURE; 21 } 22 23 Mat magI = Predft(I, complexI); 24 //Mat magI1 = Predft(I1, complexI1); 25 26 threshold(magI, magI, GRAY_THRESH, 255, THRESH_BINARY); 27 //threshold(magI1, magI1, GRAY_THRESH, 255, THRESH_BINARY); 28 imshow("spectrumed magnitude", magI); 29 translation(magI, I, complexI); 30 // imshow("Input Image", I); // Show the result 31 imshow("spectrum magnitude", magI); 32 //translation(magI1, I1, complexI1); 33 //imshow("Input Image1", I1); // Show the result 34 //imshow("spectrum magnitude1", magI1); 35 36 waitKey(); 37 destroyAllWindows(); 38 return EXIT_SUCCESS; 39 }
运行示例：
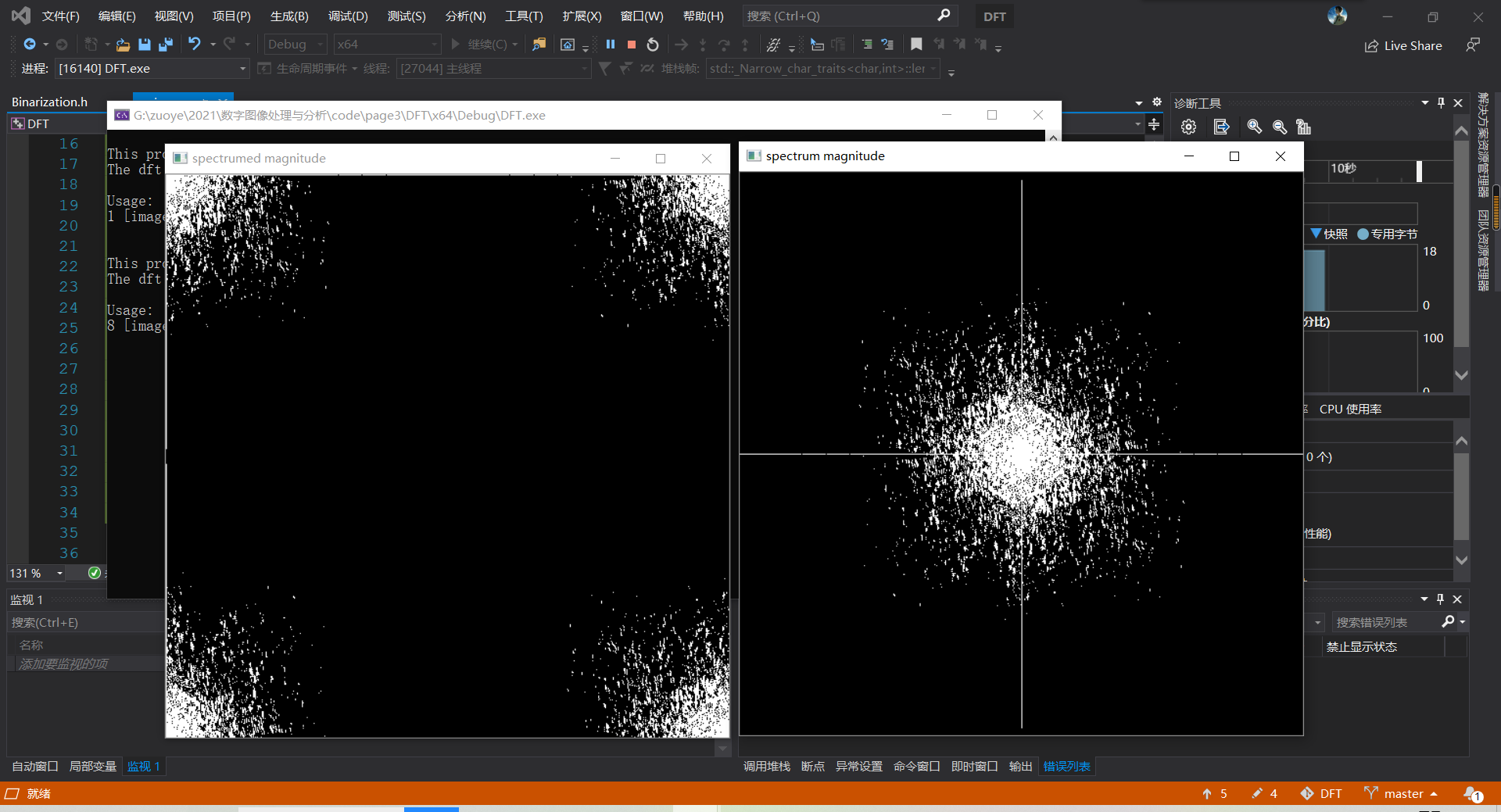
【3】旋转不变性：代码如下（头文件与上述相同；【注】旋转过程可能把图片放大了，旋转过程也是颇为有趣的）。
1 #include "Binarization.h" 2 #include <iostream> 3 4 using namespace std; 5 6 int main(int argc, char** argv) 7 { 8 char fn[] = "7.png"; 9 char fn1[] = "8.png"; 10 help(fn); 11 help(fn1); 12 Mat complexI; 13 Mat complexI1; 14 15 Mat I = imread(samples::findFile(fn), IMREAD_GRAYSCALE); 16 Mat I1 = imread(samples::findFile(fn1), IMREAD_GRAYSCALE); 17 18 if (I.empty() && I1.empty()) { 19 cout << "Error opening image" << endl; 20 return EXIT_FAILURE; 21 } 22 23 Mat magI = Predft(I, complexI); 24 Mat magI1 = Predft(I1, complexI1); 25 26 threshold(magI, magI, GRAY_THRESH, 255, THRESH_BINARY); 27 threshold(magI1, magI1, GRAY_THRESH, 255, THRESH_BINARY); 28 // imshow("spectrumed magnitude", magI); 29 translation(magI, I, complexI); 30 imshow("Input Image", I); // Show the result 31 imshow("spectrum magnitude", magI); 32 translation(magI1, I1, complexI1); 33 imshow("Input Image1", I1); // Show the result 34 imshow("spectrum magnitude1", magI1); 35 36 waitKey(); 37 destroyAllWindows(); 38 return EXIT_SUCCESS; 39 }
运行实例：
【4】比例性：代码同3。运行示例如下：
【5】中心化：中心化指在平移后频谱图中，图像的大部分信息集中在中心的位置。可以通过乘上一个(-1)x+y因子使频域中心从原点移到N×N方阵的中心。为了更好地演示中心化这个性质，有必要先介绍傅里叶的逆变换。代码如下：
1 #pragma once 2 #include "opencv2/core.hpp" 3 #include "opencv2/imgproc.hpp" 4 #include "opencv2/imgcodecs.hpp" 5 #include "opencv2/highgui.hpp" 6 #include <iostream> 7 using namespace cv; 8 using namespace std; 9 #define GRAY_THRESH 10 10 11 void help(char* argv) 12 { 13 cout << endl 14 << "This program demonstrated the use of the discrete Fourier transform (DFT). " << endl 15 << "The dft of an image is taken and it's power spectrum is displayed." << endl << endl 16 << "Usage:" << endl 17 << argv[0] << " [image_name -- default lena.jpg]" << endl << endl; 18 } 19 20 void idfft(Mat complexI, int col, int row) 21 { 22 // 使用IFFT进行反变换，得到时域图像 23 Mat ifft; 24 idft(complexI, ifft, DFT_REAL_OUTPUT | DFT_SCALE); 25 normalize(ifft, ifft, 0, 1, NORM_MINMAX); 26 imshow("idft", ifft); 27 Mat imageROI; 28 // 方法1 29 imageROI = ifft(Rect(0, 0, col, row)).clone(); 30 // cout << imageROI << endl; 31 imshow("idfft", imageROI); 32 } 33 34 Mat Predft(Mat I, Mat complexI, bool bdift = 0) 35 { 36 Mat padded; //expand input image to optimal size 37 int m = getOptimalDFTSize(I.rows); 38 int n = getOptimalDFTSize(I.cols); // on the border add zero values 39 40 //cout << m << endl; // 576 41 //cout << n << endl; // 576 42 //cout << m - I.rows << endl; // 6 43 //cout << n - I.cols << endl; // 23 44 45 copyMakeBorder(I, padded, 0, m - I.rows, 0, n - I.cols, BORDER_CONSTANT, Scalar::all(0)); 46 Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F) }; 47 48 merge(planes, 2, complexI); // Add to the expanded another plane with zeros 49 dft(complexI, complexI); // this way the result may fit in the source matrix 50 // compute the magnitude and switch to logarithmic scale 51 // => log(1 + sqrt(Re(DFT(I))^2 + Im(DFT(I))^2)) 52 split(complexI, planes); // planes[0] = Re(DFT(I), planes[1] = Im(DFT(I)) 53 magnitude(planes[0], planes[1], planes[0]);// planes[0] = magnitude 54 Mat magI = planes[0]; 55 56 // 进行对数尺度缩放 57 magI += Scalar::all(1); // switch to logarithmic scale 58 log(magI, magI); 59 60 if (bdift) // 逆变换 61 { 62 // 定义一个Mat类型并给其设定ROI区域 63 // Mat imageROI; 64 // 方法1 65 // imageROI = complexI(Rect(0, 0, I.cols, I.rows)).clone(); 66 // dft(imageROI, imageROI, DFT_COMPLEX_OUTPUT); 67 // dft(imageROI, imageROI, DFT_INVERSE); 68 // normalize(imageROI, imageROI, 0, 1, NORM_MINMAX); 69 // imshow("dft_real_output", imageROI); 70 idfft(complexI, I.cols, I.rows); 71 } 72 73 return magI; 74 } 75 76 void binar(Mat magImg) 77 { 78 threshold(magImg, magImg, GRAY_THRESH, 255, THRESH_BINARY); 79 imshow("spectrumedd magnitude", magImg); 80 } 81 82 void translation(Mat magI, Mat I, Mat complexI) 83 { 84 normalize(magI, magI, 0, 1, NORM_MINMAX); // Transform the matrix with float values into a 85 // viewable image form (float between values 0 and 1). 86 // imshow("spectrumed magnitude", magI); 87 88 // crop the spectrum, if it has an odd number of rows or columns 89 magI = magI(Rect(0, 0, magI.cols & -2, magI.rows & -2)); 90 // rearrange the quadrants of Fourier image so that the origin is at the image center 91 int cx = magI.cols / 2; 92 int cy = magI.rows / 2; 93 Mat q0(magI, Rect(0, 0, cx, cy)); // Top-Left - Create a ROI per quadrant 94 Mat q1(magI, Rect(cx, 0, cx, cy)); // Top-Right 95 Mat q2(magI, Rect(0, cy, cx, cy)); // Bottom-Left 96 Mat q3(magI, Rect(cx, cy, cx, cy)); // Bottom-Right 97 Mat tmp; // swap quadrants (Top-Left with Bottom-Right) 98 q0.copyTo(tmp); 99 q3.copyTo(q0); 100 tmp.copyTo(q3); 101 q1.copyTo(tmp); // swap quadrant (Top-Right with Bottom-Left) 102 q2.copyTo(q1); 103 tmp.copyTo(q2); 104 105 //imshow("Input Image", I); // Show the result 106 //imshow("spectrum magnitude", magI); 107 } 108 109 bool Scaling() 110 { 111 char fn[] = "7.png"; 112 char fn1[] = "9.png"; 113 cout << "输入需要比较的两幅图像：" << endl; 114 cin >> fn >> fn1; 115 116 help(fn); 117 help(fn1); 118 Mat complexI; 119 Mat complexI1; 120 121 Mat I = imread(samples::findFile(fn), IMREAD_GRAYSCALE); 122 Mat I1 = imread(samples::findFile(fn1), IMREAD_GRAYSCALE); 123 124 if (I.empty() && I1.empty()) { 125 cout << "Error opening image" << endl; 126 return false; 127 } 128 129 Mat magI = Predft(I, complexI); 130 Mat magI1 = Predft(I1, complexI1); 131 132 threshold(magI, magI, GRAY_THRESH, 255, THRESH_BINARY); 133 threshold(magI1, magI1, GRAY_THRESH, 255, THRESH_BINARY); 134 // imshow("spectrumed magnitude", magI); 135 translation(magI, I, complexI); 136 imshow("Input Image", I); // Show the result 137 imshow("spectrum magnitude", magI); 138 translation(magI1, I1, complexI1); 139 imshow("Input Image1", I1); // Show the result 140 imshow("spectrum magnitude1", magI1); 141 return true; 142 }
1 #include "Binarization.h" 2 #include <iostream> 3 4 using namespace std; 5 6 int main(int argc, char** argv) 7 { 8 char fn[] = "1.png"; 9 help(fn); 10 Mat complexI; 11 Mat I = imread(samples::findFile(fn), IMREAD_GRAYSCALE); 12 // cout << I << endl; 输出较慢 13 Mat magI = Predft(I, complexI, 1); // dft, 当是1时输出逆变换 14 threshold(magI, magI, GRAY_THRESH, 255, THRESH_BINARY); // 二值化 15 translation(magI, I, complexI); // 输出 16 imshow("Input Image", I); // Show the result 17 imshow("spectrum magnitude", magI); // 频谱图 18 // if (!Scaling()) 19 // cout << "输入有误！" << endl; 20 waitKey(); 21 destroyAllWindows(); 22 return EXIT_SUCCESS; 23 }
运行示例：（注：因为在进行dft的过程中增加了图像矩阵的维度，所以idft图像存在黑边。因此博主做了ROI区域化的处理，得到idfft图。）显然尽管频域中心发生了位移，图像并未发生明显的改变。
除此之外，本文还做了一些傅里叶变换在图像处理中的简单应用。傅里叶变换可以对图像的频谱进行各种各样的处理，如滤波、降噪、增强等。
参考文献
[1] 张弘.数字图像处理与分析[M].北京,机械工业出版社.2013.3(2017.6重印).
--------------------------------------------------------------continue-------------------------------------------
【zlc】
