Matlab拟合

实验目的

　　（1）掌握曲线拟合的相应算法；

　　（2）将拟合与插值法进行比较。

实验要求

　　实验步骤要有模型建立，模型求解、结果分析。

实验内容

　　（1）用给定的多项式，如y=x3-6x2+5x-3，产生一组数据(xi,yi，i=1,2,…,n),再在yi上添加随机干扰(可用rand产生(0,1)均匀分布随机数,或用rands产生N(0,1)分布随机数)，然后用xi和添加了随机干扰的yi作的3次多项式拟合，与原系数比较。如果作2或4次多项式拟合，结果如何？ 

　　（2）用电压V=10伏的电池给电容器充电，电容器上t时刻的电压为   ，其中V0是电容器的初始电压，  是充电常数。试由下面一组t，V数据确定V0，τ。 

t(秒)

0.5

1

2

3

4

5

7

9

V(伏)

6.36

6.48

7.26

8.22

8.66

8.99

9.43

9.63

实验步骤

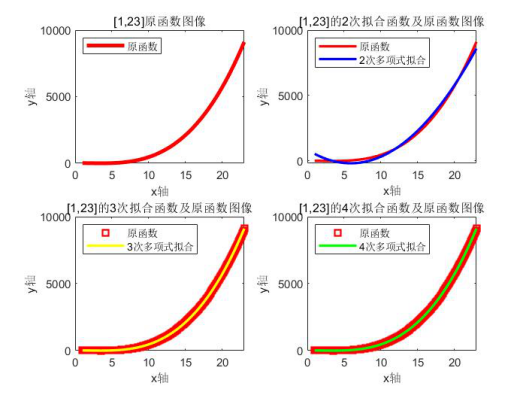
　　（1）解：编程解题，取[1,23]为例展示，代码

 1 %% 给定x，得到y
 2 x=1:0.1:23;
 3 y=x.^3-6*x.^2+5*x-3;
 4 y0=y+rand;%随机干扰
 5 %% 输出多项式系数
 6 f1=[1 -6 5 -3];%原系数
 7 f2=polyfit(x,y0,2);%2次多项式
 8 f3=polyfit(x,y0,3);%3次多项式
 9 f4=polyfit(x,y0,4);%4次多项式
10 %% 输出图像
11 % 计算各x点拟合值
12 y2=polyval(f2,x);
13 y3=polyval(f3,x);
14 y4=polyval(f4,x);
15 % 画图
16 figure,subplot(2,2,1)
17 plot(x,y,'r','LineWidth',3);%原图像
18 legend('原函数','Location','northwest');
19 title('[1,23]原函数图像');
20 xlabel('x轴');
21 ylabel('y轴');
22  
23 subplot(2,2,2)
24 plot(x,y,'r',x,y2,'b','LineWidth',1,'LineWidth',2)%2次多项式拟合
25 legend('原函数','2次多项式拟合','Location','northwest');
26 title('[1,23]的2次拟合函数及原函数图像');
27 xlabel('x轴');
28 ylabel('y轴');
29  
30 subplot(2,2,3)
31 plot(x,y,'rs',x,y3,'y','LineWidth',1,'LineWidth',2)%3次多项式拟合
32 legend('原函数','3次多项式拟合','Location','northwest');
33 title('[1,23]的3次拟合函数及原函数图像');
34 xlabel('x轴');
35 ylabel('y轴');
36  
37 subplot(2,2,4)
38 plot(x,y,'rs',x,y4,'g','LineWidth',1,'LineWidth',2);%4次多项式拟合
39 legend('原函数','4次多项式拟合','Location','northwest');
40 title('[1,23]的4次拟合函数及原函数图像');
41 xlabel('x轴');
42 ylabel('y轴');
43  
44  
45
题1_MATLAB

　　程序运行

　　原系数：1，-6，5，-3；

　　二次拟合系数：30，-353.7420，846.8601；

　　三次拟合系数：1，-6，5，-2.0439；

　　四次拟合系数：-4.6603e-17，1，-6，5，-2.0439。

　　右上述运行的结论，得出三次拟合系数与原系数相差不大，只有常数项不一样；四次系数的四次项的系数几乎为0，而接下来的系数与原系数相差就在常数项中；只有二次拟合的系数相差巨大。

　　由图可见，三次多项式和四次多项式的拟合效果较好。二次多项式拟合效果较差。

　　（2）解：根据题意得，v(t)与T呈指数变化关系，本报告使用指数曲线拟合（非线性拟合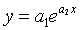），对题干中的变量做新的阐述，v1代替v(t)，t0代替τ，v2是拟合后的曲线方程，对v(t)=v-(v-v0)e(-t/τ)取对数，有令 ，，则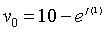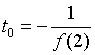，。编程解题，代码

 1 %题2
 2 t=[0.5 1 2 3 4 5 7 9];
 3 v1=[6.36 6.48 7.26 8.22 8.66 8.99 9.43 9.63];
 4 y=log(10-v1);
 5 f=polyfit(t,y,1);
 6 t0=-1/f(1);
 7 v0=10-exp(f(2));
 8 v2=10-(10-v0)*exp(-t/t0);
 9 plot(t,v1,'rx',t,v2,'k:','LineWidth',2,...
10     'LineWidth',2);
11 grid on
12 legend('原始数据','曲线拟合','Location','northwest');
13 xlabel('时间t(s)'),ylabel('充电电压(V)');
14 title('电容器充电电压与时间t的曲线');
15
题2_MATLAB

　　运行示例，

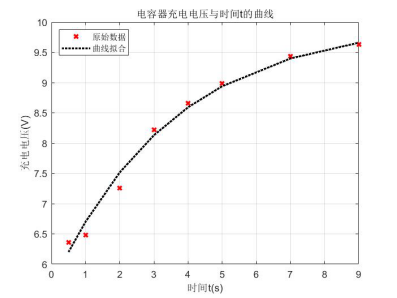
 　　由图示，拟合效果良好，解得t0=3.5269，v0=5.6221。也就是τ=3.5269。

小结

 　　使用曲线拟合之前最好对该曲线的的可能拟合的方程做大致的估计，并且在拟合完成之后，应当使用其他数据进行检验。

 

posted @ 2020-05-24 12:01  望星草  阅读(1547)  评论(0)  编辑  收藏  举报