Matlab非线性方程数值解法（2）

实验目的

　　用Matlab实现非线性方程的Aitken加速法、牛顿法、简化牛顿法和牛顿下山法。

实验要求

  1. 　　给出Aitken加速法、牛顿法、简化牛顿法和牛顿下山法算法。
  2. 　　 用Matlab实现Aitken加速法、牛顿法、简化牛顿法和牛顿下山法。

实验内容

 实验步骤

（1）Aitken加速算法，

　　MATLAB编程，

 1 %Aitken算法
 2 %迭代函数fun，初始值x，精度ep，最大迭代次数Nmax。
 3 %满足精度（或已达到最大迭代次数）的近似根root，迭代次数k。
 4 function [root,k]=Aitken(fun,x,ep,Nmax)
 5 %默认迭代次数和默认精度
 6 if nargin<4
 7     Nmax=500;
 8 end
 9 if nargin<3
10     ep=1e-5;
11 end
12 %初始化
13 k=0;
14 r(1,1)=x;
15 %迭代
16 while abs(x-fun(x))>ep
17     xk=x;
18     x=fun(x);
19     x1=x;
20     x=fun(x);
21     x2=x;
22     x=x2-(x2-x1)^2/(x2-2*x1+xk);
23     k=k+1;
24     r(k+1,1)=x;
25 end
26 %root=x;
27 root=r(:,1);
28 if k==Nmax
29     warning('已迭代上限次数');
30 end
31 end
Aitken.m

　　运行示例（为了减小篇幅，初始值的选取由下面的讨论得到），

　　

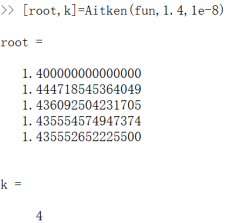
　　当初始值为10时，节选截图,

　　

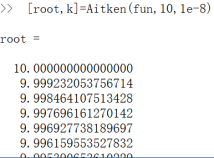
 　　可见该算法迭代了3610次，这个结果的好坏需要与其他算法对比，使用上一个实验所编写的bisect3.m（改进的二分法）：

　　

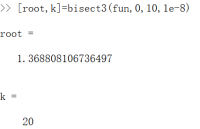
 　　可见迭代20次，已经接近所要求的近似根了。

　　为了了解该算法的特点，本报告对算法进行修改：缩小区间，再使用Aitken算法迭代。分析：易知上述到Aitken算法的时间复杂度与精度有关（O(g(e))，e的变化受迭代函数影响），初始值越接近所要求的近似根，运算的步骤越少。所以对初始值做处理是有必要的，这里如果使用20次2分法预报初值时，精度可以达到0.5^20，约1e-6。

 1 %Aitken1算法
 2 %迭代函数fun，初始值x，精度ep，最大迭代次数Nmax。
 3 %满足精度（或已达到最大迭代次数）的近似根root，迭代次数k。
 4 function [root,k]=Aitken1(fun,n,ep,Nmax)
 5 %默认迭代次数和默认精度
 6 if nargin<4
 7     Nmax=500;
 8 end
 9 if nargin<3
10     ep=1e-5;
11 end
12 [x,k]=bisect3(fun,0,n,1e-4);
13 if abs(fun(x))<ep
14     root=x;
15     k=0;
16     return;
17 end
18 %初始化
19 r(1,1)=x;
20 %迭代
21 while abs(x-fun(x))>ep
22     xk=x;
23     x=fun(x);
24     x1=x;
25     x=fun(x);
26     x2=x;
27     x=x2-(x2-x1)^2/(x2-2*x1+xk);
28     k=k+1;
29     r(k+1,1)=x;
30 end
31 %root=x;
32 root=r(:,1);
33 if k>=Nmax
34     warning('已迭代上限次数');
35 end
36 end
Aitken1.m
 1 %二分法改良
 2 %在一开始给定的区间中寻找更小的有根区间
 3 %输入：f(x)=0的f(x)，[a,b]的a,b，精度ep
 4 %输出：近似根root，迭代次数k
 5 %得到的根是优化区间里的最大根
 6 function [root,k]=bisect3(fun,a,b,ep)
 7 if nargin>3
 8     elseif nargin<4
 9         ep=1e-5;%默认精度
10     else
11         error('输入参数不足');%输入参数必须包括f(x)和[a,b]
12 end
13 %定义划分区间的分数
14 divQJ=1000;
15 %等分区间
16 tX=linspace(a,b,divQJ);
17 %计算函数值
18 tY=fun(tX);
19 %找到函数值的正负变化的位置
20 locM=find(tY<0);
21 locP=find(tY>0);
22 %定义新区间
23 if tY(1)<0
24 a=tX(locM(end));
25 b=tX(locP(1));
26 else
27 a=tX(locP(end));
28 b=tX(locM(1));
29 end
30 if fun(a)*fun(b)>0%输入的区间要求
31     root=[fun(a),fun(b)];
32     k=0;
33     return;
34 end
35 k=1;
36 while abs(b-a)/2>ep%精度要求
37     mid=(a+b)/2;%中点
38     if fun(a)*fun(mid)<0
39         b=mid;
40     elseif fun(a)*fun(mid)>0
41         a=mid;
42     else
43         a=mid;b=mid;
44     end
45     k=k+1;
46 end
47 root=(a+b)/2;
48 end
bisect3.m

　　运行示例，

　　

 　　0的部分表示调用bisect3.m（精度要求1e-4），在bisect3.m迭代的次数为7，在Aitken部分迭代的次数为5。总共迭代12次远比3610次小。

　　对【题目】的解答，为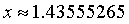　　 MATLAB编程，

 1 %牛顿法
 2 %输入：迭代函数fun,迭代函数的导函数dfun，初始值x，精度ep，最大迭代值Nmax。
 3 %输出：近似根root，迭代次数k，迭代成功与否index。
 4 function [root,k]=Newton2(fun,dfun,x0,ep,Nmax)
 5 %默认迭代次数和默认精度
 6 if nargin<5
 7     Nmax=500;
 8 end
 9 if nargin<4
10     ep=1e-5;
11 end
12 %初始化
13 k=0;
14 x=x0;x0=x+2*ep;
15 %迭代
16 while abs(x0-x)>ep
17     k=k+1;
18     x0=x;
19     x=x0-fun(x0)/dfun(x0);
20 end
21 root=x;
22 if k>=Nmax
23     warning('已迭代上限次数');
24 end
25 end
Newton2

　　运行示例，

　　

 　　所以解得【题目】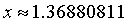，（与上述的改进二分法求得的结果相近）。

 　　MATLAB程序，

 1 %牛顿平行弦法
 2 %输入：迭代函数fname，迭代函数的一阶导函数dfname，初始值x0，精度ep，最大迭代值Nmax。
 3 %输出：近似根root，迭代次数k，迭代成功与否index。
 4 function [root,k,index]=newton4(fname,dfname,x0,ep,Nmax)
 5 %默认迭代次数和默认精度
 6 if nargin<5
 7     Nmax=500;
 8 end
 9 if nargin<4
10     ep=1e-5;
11 end
12 %初始化
13 index=0;k=1;c=1/dfname(x0);x=x0;
14 while k<Nmax
15     x1=x-c*fname(x);
16     if abs(x1-x)<ep
17         break;
18     end
19     x=x1;
20     k=k+1;
21 end
22 if 0<c*dfname(x) && c*dfname(x)<2
23     root=x;
24     index=1;
25 else
26     root=x;
27     index=0;
28     disp('不满足收敛条件');
29 end
30 if k==Nmax
31     warning('已迭代上限次数');
32 end
33 end
newton4

　　运行示例，

　　

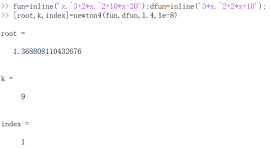
 　　所以解得【题目】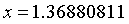，（效果与牛顿法相近）。

　　MATLAB编程，

 1 %牛顿下山法
 2 %输入：迭代函数fname，迭代函数的一阶导函数dfname，初始值x0，精度ep，最大迭代值Nmax。
 3 %输出：近似根root，迭代次数k，%此处不展示函数迭代值单调变化f。
 4 function [root,k]=newton3(fname,dfname,x0,ep,Nmax)
 5 %默认迭代次数和默认精度
 6 if nargin<5
 7     Nmax=500;
 8 end
 9 if nargin<4
10     ep=1e-5;
11 end
12 %初始化
13 k=0;x=x0-fname(x0)/dfname(x0);
14 %f=abs(fname(x0));
15 %迭代
16 while abs(x0-x)>ep && k<Nmax
17     k=k+1;
18     r=1;
19     while abs(fname(x))>abs(fname(x0))
20         r=r/2;
21         x=x0-r*fname(x0)/dfname(x0);
22         if abs(fname(x))<abs(fname(x0))
23             break;
24         end
25     end
26     x0=x;
27     x=x0-fname(x0)/dfname(x0);
28     %f=abs(fname(x0));
29 end
30 root=x;
31 if k==Nmax
32     warning('已迭代上限次数');
33 end
34 end
newton3

　　运行示例，

　　

　　所以，解得【题目】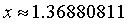，（效果与牛顿法相差不大）。

 　　总结解得的近似根，

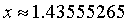  1. 　　,代入原式，1.4355526.
  2. 3.4.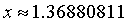,代入原式，-1.009655。总体来说，后面3种算法都比第1种算法更高效。 

 小结

　　在解第1题时，本报告对初始值的选取进行了一些讨论。使用二分法锁定耙子固然简单，但是二分法对区间也是有要求，起码是有根区间（在改进二分法中有根区间的限制可以放宽一点），例如，上题我的修改是（0到n）作为瞄准的区间，如果该题的根在负轴上呢？总而言之，初始值的优选区间也是一个值得讨论的问题。第2个值得讨论的问题是，不同算法的混用能否获得更好的结果？

 

posted @ 2020-05-13 17:19  望星草  阅读(951)  评论(0)  编辑  收藏  举报