SPSS非参数检验

实验目的：

学会使用SPSS的简单操作，掌握非参数检验。

实验内容：

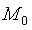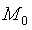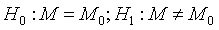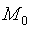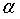　　1.中位数符号检验，检验总体中位数是否等于某个假定的值。设一个随机样本有n个数据，总体中位数的实际值为M，假设的总体中位数值为。当样本中的数据大于假设的中位数时，用“+”号表示，小于假设的中位数时，用“-”表示；对于恰好等于假设的中位数的数据予以剔出。若关心实际的M与假设的是否有差别，应建立假设：；计算检验统计量S+和S-。S+表示每个样本数据与与差值符号为正的个数；S-表示每个样本数据与差值符号为负的个数。计算P值并作出决策。若P<，拒绝原假设。

 

　　2.Wilcoxon符号秩检验，检验总体参数(如中位数)是否等于某个假定的值。它是对符号检验的一种改进，弥补了符号检验的不足，要比单纯的符号检验更准确一些(对应的参数检验—单样本均值检验)。检验步骤：①计算各样本观察值与假定的中位数的差值，并取绝对值；②将差值的绝对值排序，并找出它们的秩；③计算检验统计量和P值，并作出决策。 

 

　　3.独立样本的检验，Mann-Whitney检验不需要诸如总体服从正态分布且方差相同等之类的假设，但要求是两个独立随机样本的数据至少是顺序数据；Kruskal-Wallis检验不需要总体服从正态分布且方差相等这些假设。该检验可用于顺序数据，也可用于数值型数据 。要检验k个总体是否相同，提出如下假设。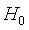：所有总体都相同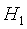，：并非所有总体都相同或等价于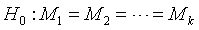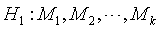，不全相同。

 

　　4.秩相关检验，对两个顺序变量之间相关程度的一种度量。Spearman秩相关系数也称等级相关系数，记为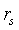，计算公式为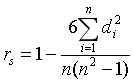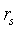，的取值范围为[-1,1]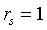；，两种排序之间完全相关；若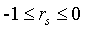，两种排序之间为负相关；若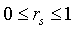，两种排序之间为正相关；若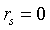，两种排序之间不相关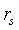；越趋于1，相关程度越高；越趋于0，相关程度越低。

实验步骤：

 

　　1.中位数符号检验SPSS操作，点击【分析】→【非参数检验】→【相关样本】，打开【非参数检验、两个或更多相关样本】对话框。【字段】选入要检验的字段列；【设置】可以选择【根据数据自动选择检验】，也可以切换为【定制检验】，选择【符号检验】。单击【运行】，（默认α=0.05，可以在【设置】的【检验选项】修改）。

 

 　　

 

 　　

 

 　　

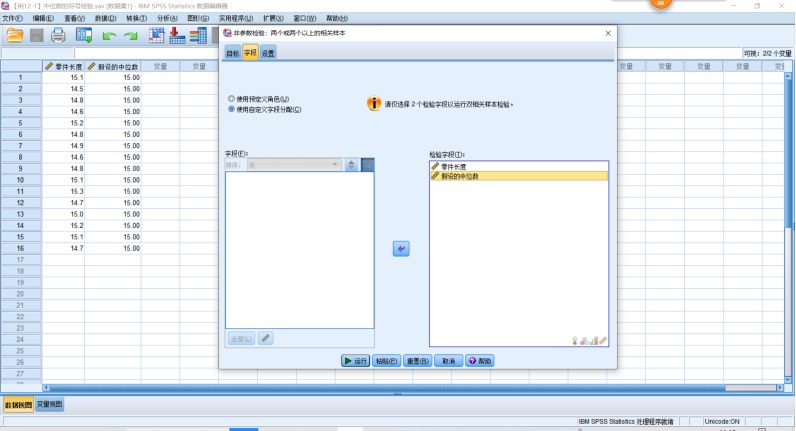
　　因为二者符号检验的显著性为0.607>0.05，不拒绝原假设，没有证据表明该企业生产的零件的实际中位数与15cm有显著差异。

 

 

1 *Nonparametric Tests: Related Samples.
2 NPTESTS
3 /RELATED TEST(零件长度 假设的中位数) SIGN
4 /MISSING SCOPE=ANALYSIS USERMISSING=EXCLUDE
5 /CRITERIA ALPHA=0.05  CILEVEL=95.
中位数符号检验

　　2.Wilcoxon符号秩检验SPSS操作，基本同上在【设置】中的【自定义检验】选择【Wilcoxon匹配对符号秩】。也可以使用旧对话框，【旧对话框】→【两个关联样本检验】→【Wilcoxon(W)】。

　　

 

 　　

 

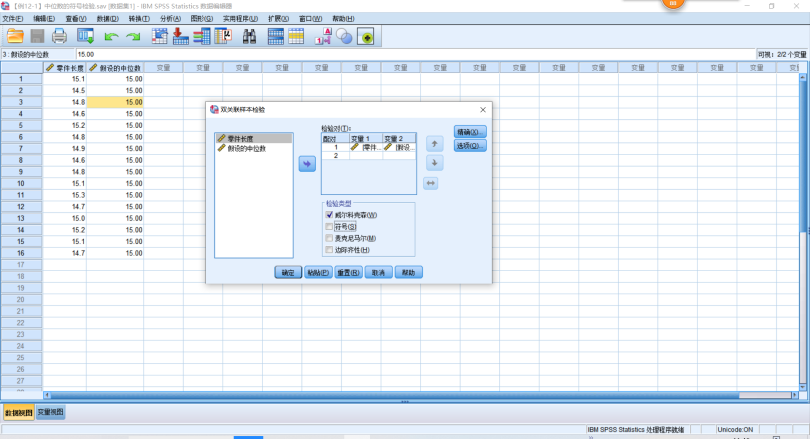
 　　渐进的双尾检验概率为0.116，不拒绝原假设，没有证据表明零件的实际中位数与15cm有显著差异。

 

1 NPAR TESTS
2 /WILCOXON=零件长度 WITH 假设的中位数 (PAIRED)
3 /MISSING ANALYSIS.
Wilcoxon符号秩检验

 

　　

 

 　　

 

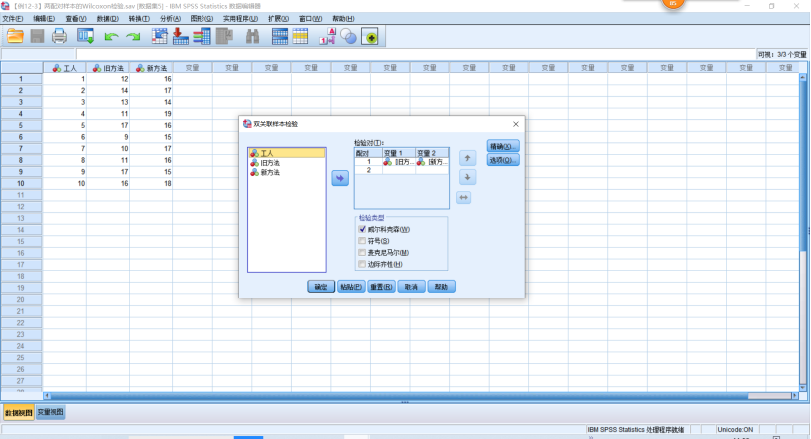
 　　统计量为-2.296，渐进的双尾P=0.022<0.05，拒绝，两种方法生产的产品数量有显著差异

1 NPAR TESTS
2 /WILCOXON=旧方法 WITH 新方法 (PAIRED)
3 /MISSING ANALYSIS.
Wilcoxon符号秩检验2

　　4.独立样本的检验SPSS操作，【分析】→【非参数检验】→【独立样本】，在打开的对话框中，【字段】设置使用定制字段分配，把相应变量选入【检验字段列表框】和【组变量列表框】。可默认使用【根据数据自动选择检验】，也可切换为【自定义检验】，选择M-W U检验，点击【运行】。也可以使用旧对话框按钮，【分析】→【非参数检验】→【旧对话框】→【两个独立样本】，在打开的对话框中设置好【检验变量列表】框和【分组变量】列表框，【定义组】设置组1为组1，组2为组2，【继续】。单击【确定】。多个独立样本的检验，【分析】→【非参数检验】→【独立样本】，在打开的对话框中，【字段】设置好相应的【检验字段】和【组变量】选入【time】，选择【K-W ANOVA】检验，多重比较采用默认的【所有成对比较】，单击【运行】。使用旧对话框也可以。

 

 

　　

 

 　　

 

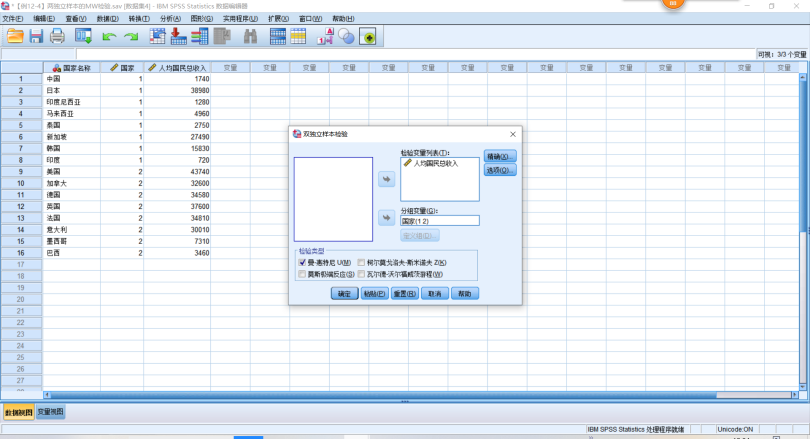
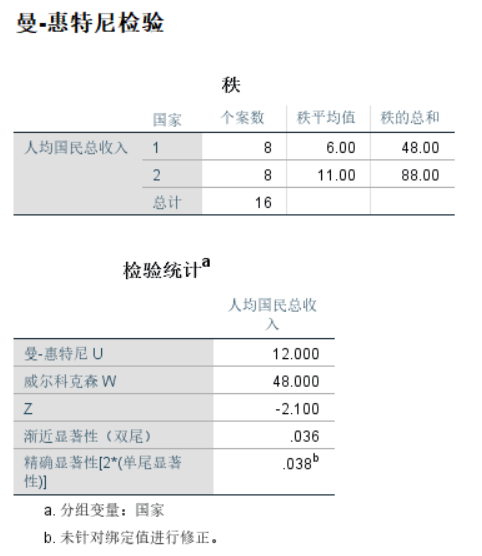
 　　因为统计量为-2.100，渐进的双尾0.036，拒绝，亚洲国家和欧美国家的人均国民收入有显著差别。

 

1 NPAR TESTS
2       /M-W= 人均国民总收入 BY 国家(1 2)
3       /MISSING ANALYSIS.
曼-惠特尼检验

 

　　

 

 　　

 

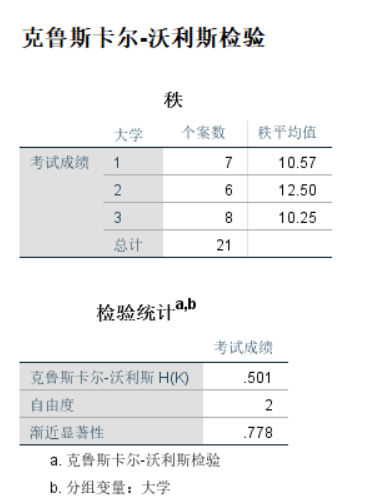
 　　因为渐进到双尾P值为0.778，不拒绝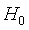，没有证据表明3所大学对的英语考试成绩之间存在显著差异。

1 NPAR TESTS
2     /K-W=考试成绩 BY 大学(1 3)
3     /MISSING ANALYSIS.
K-W检验

　　4.秩相关检验SPSS操作，【分析】→【相关】→【双变量】，在【双变量相关性】窗口，将需要进行相关性分析的变量拖入到【变量】列表框中，勾选相关系数为【Spearman】→【双尾检验】→【标记显著性相关】，单击【确定】。

　　

 

 　　

 

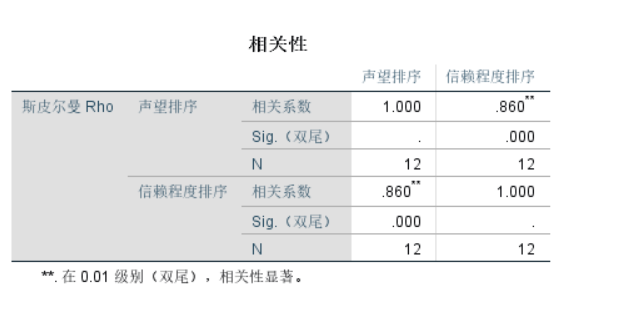
 　　因为Spearman秩相关系数为0.860，两种排序之间有较高的正相关，即职业声望越高，值得信赖的程度越高。双尾检验的P=0.000，拒绝原假设，表明声望排序与信赖程度排序之间存在显著的相关关系。

1 NONPAR CORR
2   /VARIABLES=声望排序 信赖程度排序
3   /PRINT=SPEARMAN TWOTAIL NOSIG
4   /MISSING=PAIRWISE.
Spearman秩相关检验

 

小结：

（1）中位数检验，检验各个样本是否来自具有相同中位数的总体，它的检验效能较低，但对于厚尾的对称分布该方法较为有效。

（2）关于两个样本的非参数检验，Mann-Whitney U是检验功效最强、应用范围最广的非参数检验。其零假设和备择假设的基础是：如果两个样本有差异，它们的中心位置将不同。

 

posted @ 2020-05-02 18:22  望星草  阅读(4201)  评论(0)  编辑  收藏  举报