线性规划问题（一）

实验目的：

　　通过实验，使学生了解LINGO软件的基本功能，掌握LINGO软件的求解过程，以及熟悉LINGO软件的主要菜单命令,能用LINGO软件解线性规划问题。

实验要求：　　

　　实验步骤要有模型建立，模型求解、结果分析。

实验内容：

　　（1）某厂生产甲、乙两种产品，这两种产品均需要A、B、C三种资源，每种产品的资源消耗量及单位产品销售后所能获得的利润值以及这三种资源的储备如下表所示：

　　

	A	B	C
甲	9	4	3	70
乙	4	6	10	120
	360	200	300

　　试建立使得该厂能获得最大利润的生产计划的线性规划模型。

 

　　（2）某公司生产甲、乙两种产品，生产所需原材料、工时和零件等有关数据如下：

　　

	甲            乙	可用量
原材料（吨/件） 工时（工时/件） 零件（套/件）	2            2 5            2.5 1	3000吨 4000工时 500套
产品利润（元/件）	4               3

　　建立使利润最大的生产计划的数学模型。

　　

　　（3）战术决策问题，某战略轰炸机队指挥官得到了摧毁敌方坦克生产能力的命令. 根据情报, 敌方有四个生产坦克部件的工厂, 位于不同的地方. 只要破坏其中任一工厂的生产设施就可以有效地停止敌方坦克的生产. 根据分析, 执行该任务的最大因素是汽油短缺, 为此项任务只能提供48000加仑汽油.而对于任何一种轰炸机来说, 不论去轰炸哪一个工厂都必须有足够往返的燃料和100加仑备余燃料.该轰炸机队现有重型和中型两种轰炸机, 其燃油消耗量及数量见下表

　　

 

 

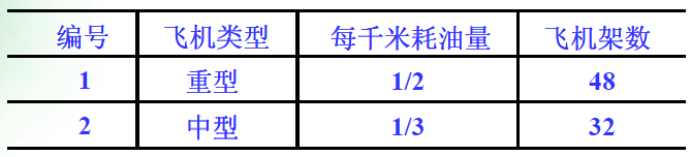
 　　各工厂距离空军基地的距离和摧毁目标的概率见下表

　　

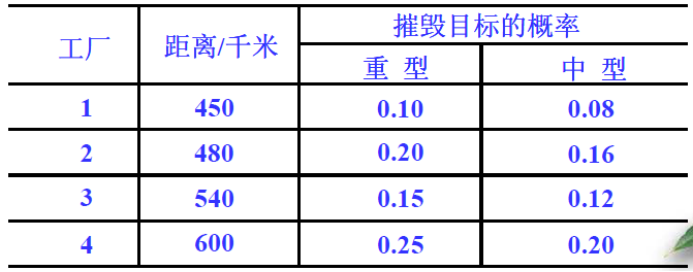
　　试问: 指挥官应向四个工厂派遣每种类型的飞机各多少架去执行任务才能使成功的概率最大?

 

实验步骤：

　　

 

 

 　　使用Lingo求解，

　　

model:
max=70*x1+120*x2;
9*x1+4*x2<=360;
4*x1+6*x2<=200;
3*x1+10*x2<=300;
@gin(x1);!整数化;
@gin(x2);
end

　　

 

 

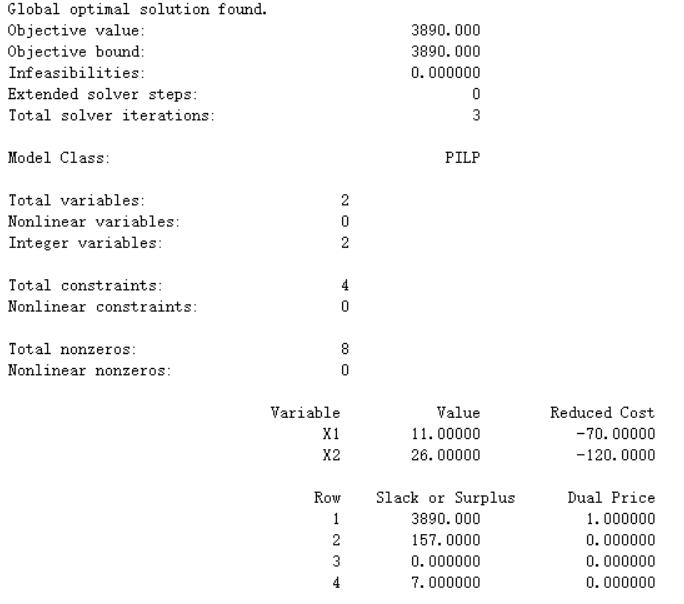
 　　解得，甲产品生产11件，乙产品生产26件时，获得的利润最大，为3890。

 

 

 

 　　使用Lingo求解，

 

model:
max=4*x1+3*x2;
2*x1+2*x2<=3000;
5*x1+2.5*x2<=4000;
x1<=500;
@gin(x1);
@gin(x2);
end

 

　　 

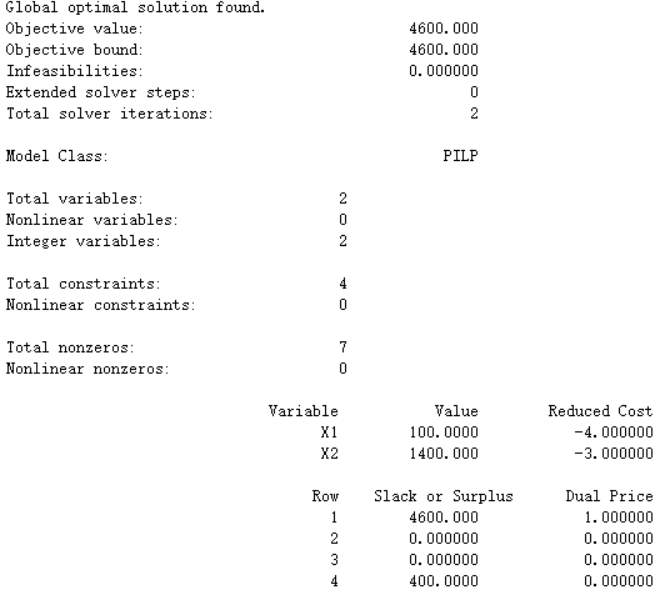
　　解得，甲产品生产100件，乙产品生产1400件时，获得的利润最大，为4600。

 

　　使用Lingo求解，（对目标函数做连乘变连加的处理），

 

model:
sets:
plane/1..2/:a,b;
factory/1..4/:d;
link(plane,factory):p,x;
endsets
data:
a=0.5 0.3333;
b=48 32;
p=0.1 0.2 0.15 0.25
0.08 0.16 0.12 0.2;
enddata
min=@sum(link:x*@log(1-p));
2*@sum(link(i,j):a(i)*d(j)*x(i,j))+100*@sum(link:x)<48000;
@for(plane(i):@sum(factory(j):x(i,j))<b(i));
@for(link:@gin(x));
end

 

　　

 

 

 　　求得48台1型飞机到4号工厂，32台2型飞机到4号工厂执行任务成功的概率最大。

 

小结：

　　使用Lingo求解线性问题使用的语句几乎与日常我们书写的式子一般，使用起来非常直观，较为方便。它输出的信息是较为丰富的。而在求解非线性问题时也较为方便。