SPSS假设检验
实验目的:
1、学会使用SPSS的简单操作。
2、掌握假设检验。
实验内容:
1.一个总体均值的检验(小样本);
2.两个总体均值之差的检验;
3.绘制正态概率图;
4.S—W检验。
实验步骤:
1.一个总体均值的检验(小样本):单总体的Z检验和t检验。设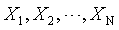 是取自正态总体
是取自正态总体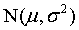 的一个样本,要检验
的一个样本,要检验 。其中
。其中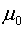 为已知的常数。为了说明如何构造检验统计量和拒绝域,先看一个简单的情形。设总体方差是已知的,记为
为已知的常数。为了说明如何构造检验统计量和拒绝域,先看一个简单的情形。设总体方差是已知的,记为 ,设
,设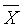 为样本均值,则
为样本均值,则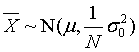 。设
。设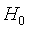 为真,即
为真,即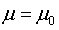 ,对
,对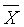 作标准化,得到
作标准化,得到 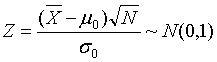
上述的Z就是要构造的检验统计量。设定显著性水平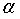 为0.05,因为
为0.05,因为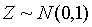 ,
,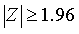 的概率为0.05,所以检验的拒绝域是
的概率为0.05,所以检验的拒绝域是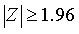 。如果由样本计算得到
。如果由样本计算得到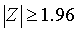 ,与小概率原理矛盾,从而拒绝原假设。
,与小概率原理矛盾,从而拒绝原假设。
在实际应用中,总体的方差是未知的。因而需要样本方差代替总体方差,相应地,检验统计量编程了t统计量。设 与
与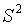 分别为样本的均值和样本方差,当
分别为样本的均值和样本方差,当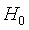 为真时,可知统计量
为真时,可知统计量
对于给定的显著性水平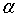 ,检验的拒绝域是
,检验的拒绝域是 。其中临界值
。其中临界值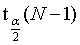 满足条件
满足条件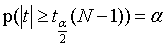 。它就是自由度为(N-1)的t分布的双侧
。它就是自由度为(N-1)的t分布的双侧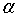 分为点。如果由样本观测值代入,计算得到的t值满足,则拒绝原假设。
分为点。如果由样本观测值代入,计算得到的t值满足,则拒绝原假设。
SPSS检验结果不给出临界值,而是在给出t值的同时给出它的显著性概率(也成为p值或相伴概率,记为p或Sig)。计算一个双侧检验问题,SPSS操作如下:“分析”→“比较均值”→“单样本T检验”,在打开的对话框中填好“检验变量”列表框和“检验值”文本框。单击“确定”。输出结果中的Sig.(双侧)就是p值。比较p值与检验水准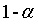 。
。
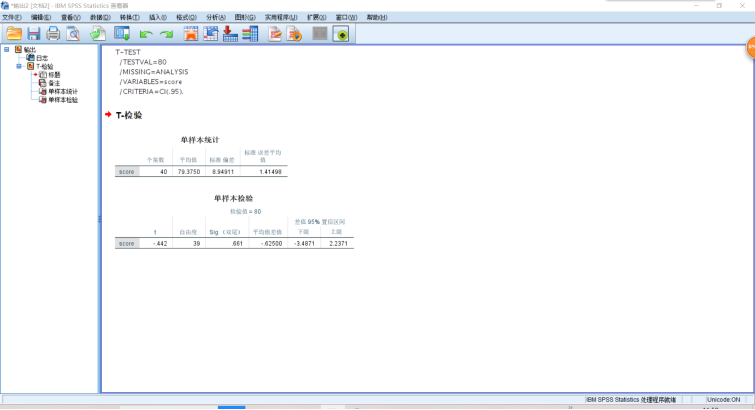

1 T-TEST 2 /TESTVAL=80 3 /MISSING=ANALYSIS 4 /VARIABLES=score 5 /CRITERIA=CI(.95).

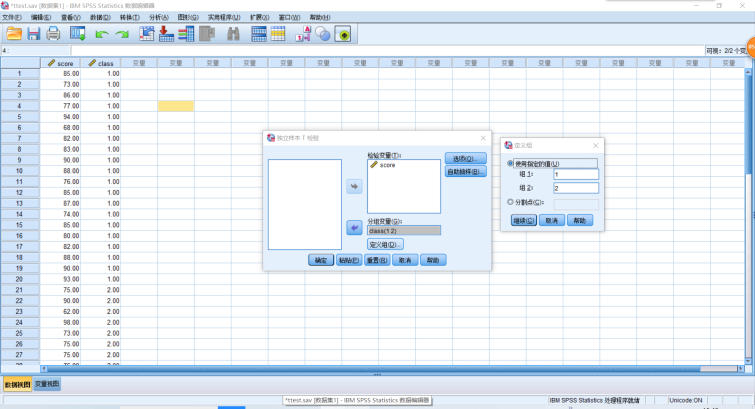
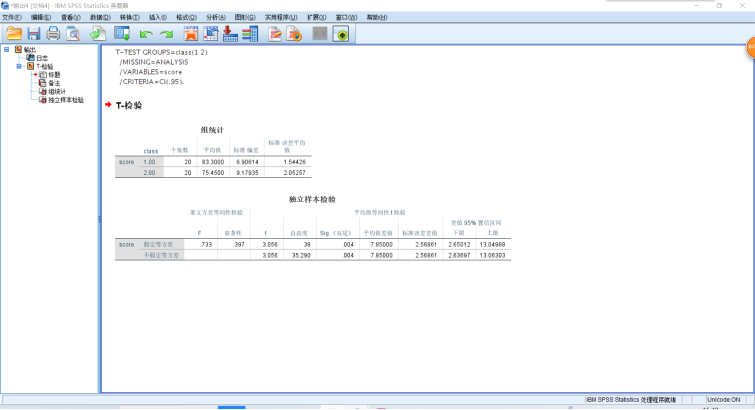
差齐性检验:Sig=0.397>0.05,方差不显著,可以认为两个独立样本的方差一致。均值之差t检验:在方差相等的条件下,Sig=0.004<0.05,均值之差显著,可以认为两个独立样本均值有显著差异。

1 T-TEST GROUPS=class(1 2) 2 /MISSING=ANALYSIS 3 /VARIABLES=score 4 /CRITERIA=CI(.95).
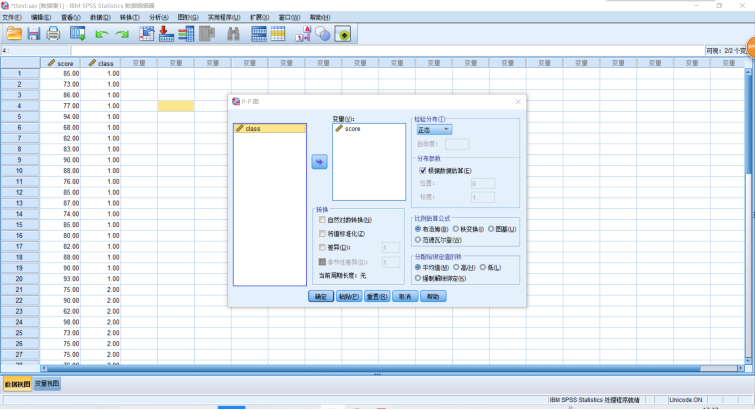
3.绘制正态概率图;P-P图和Q-Q图最常用于判断变量是否服从正态分布,但实际上他们可以用于考察其它分布,常有的有BETA分布、指数分布、伽玛分布、半对数分布、拉普拉斯分布、logistic分布、对数正态分布、帕累托分布、t分布、weibull分布、标准正态分布等共13种分布。从P-P图中可以看出变量的实际累积概率与其假定理论分布累计概率的符合程度,从而判断是否服从所考察的分布类型。如果变量服从理论分布,则实际累积概率与理论累积该理念应该基本一致。操作如下:“分析”→“描述统计”→“P-P图”,在打开的对话框中,选择需要分析的变量。在“检验分布”的下拉菜单中,选择“正态”。“转换”框组提供了4中数据变换方法,以考查变换后的数据分布情况。“比例估计公式”框组,用于估计样本累计概率分布的具体算法,一般不需要修改。“分配给绑定值的秩”,指定样本中出现冲符数值时的处理方式,默认的均值就非常合适,不需要更改。
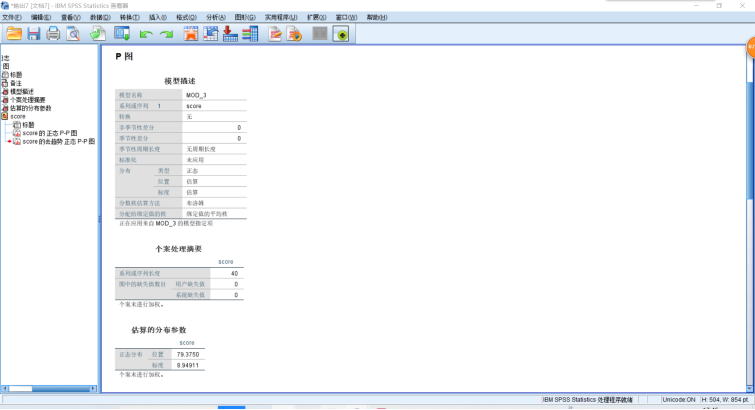

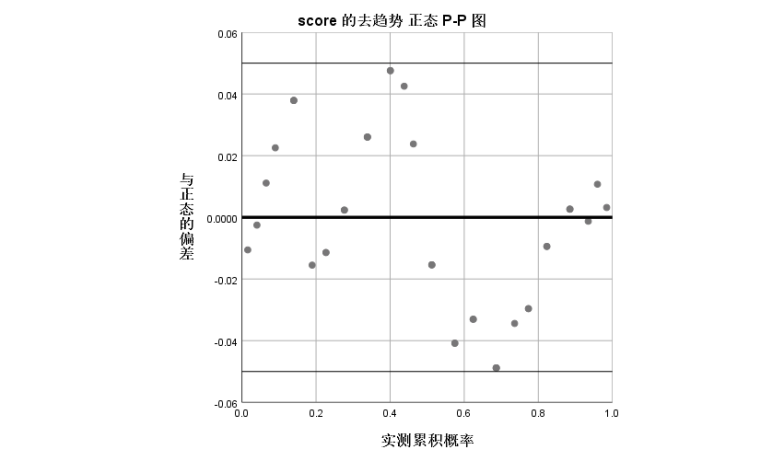
如果数据服从正态分布,则其中的数据点迎合理论直线(对角线)基本重合。可见score的实际分布和理论分布较为接近。为了更仔细的观察,可以继续观察趋势P-P图,该图反映的是按正态分布计算的理论值和实际值之差的分布情况,即分布的残差图。如果数据服从正态分布,则数据应交均匀地分布在Y=0这条直线的上下。从图中可见残差虽有一定的上下波动,但是绝对差异均小于0.05,这在绝大多数研究中都是可以忽略的分布概率差异。由此可以看出,变量score原始数据与正态分布的理论数据相差很小,可以认为其基本服从正态分布。(上图两条参考线分别是Y=0.05和Y=-0.05,是在输出窗口里双击该图,在编辑窗口里添加的)

1 PPLOT 2 /VARIABLES=score 3 /NOLOG 4 /NOSTANDARDIZE 5 /TYPE=P-P 6 /FRACTION=BLOM 7 /TIES=MEAN 8 /DIST=NORMAL.
Q-Q图也用于比较变量的实际分布与其假定的理论分布是否一致。但P-P图比较的是两者的累计概率分布,而Q-Q图则是根据变量的实际百分位数域理论百分数进行绘制的,或者说得更通俗一点,相比之下,Q-Q图的适用条件更加宽松,结果也更稳健一些。但是Q-Q图进行观察时存在一个很大的问题,即不想P-P图可以用经验界值来判断样本是否和理论分布存在明显差异,因此应用相对较少。操作:“分析”→“描述统计”→“Q-Q图”,操作与P-P图的操作基本一致。

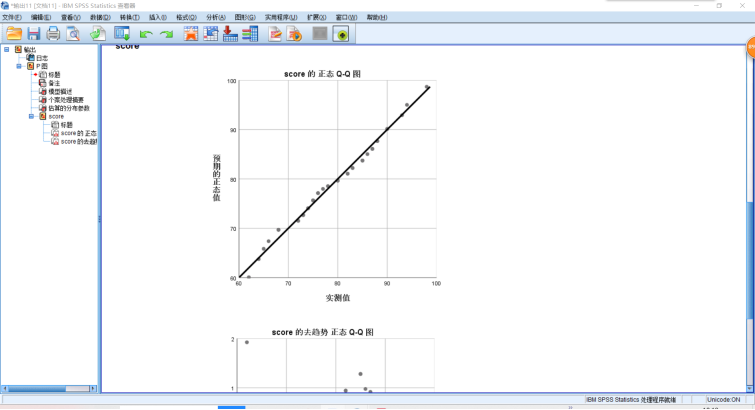

1 PPLOT 2 /VARIABLES=score 3 /NOLOG 4 /NOSTANDARDIZE 5 /TYPE=Q-Q 6 /FRACTION=BLOM 7 /TIES=MEAN 8 /DIST=NORMAL.

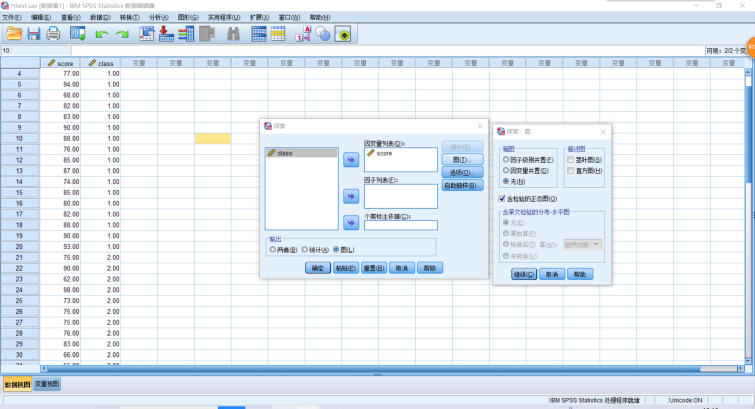

一般以Sig.(显著性)值大于0.05,就可以说明数据是正态性的。

1 EXAMINE VARIABLES=score 2 /PLOT NPPLOT 3 /STATISTICS NONE 4 /CINTERVAL 95 5 /MISSING LISTWISE 6 /NOTOTAL.
小结:
(1)假设检验的理论基础是“小概率反证法”原理,无论多复杂的检验方法,期分析的逻辑都是该原理。
(2)假设检验设计的几个概念:原假设,备择假设;第一类错误,第二类错误;显著性水平;单尾检验,双尾检验。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号