Matlab数据的统计分析与描述
实验目的
(1)熟悉统计的基本概念、参数估计、假设检验。
(2.)会用参数估计和假设检验对实际问题进行分析。
实验要求
实验步骤要有模型建立,模型求解、结果分析。
实验内容
(1)某校60名学生的一次考试成绩如下:
93 75 83 93 91 85 84 82 77 76 77 95 94 89 91 88 86 83 96 81 79 97 78 75 67 69 68 84 83 81 75 66 85 70 94 84 83 82 80 78 74 73 76 70 86 76 90 89 71 66 86 73 80 94 79 78 77 63 53 55
1)计算均值、标准差、极差、偏度、峰度,画出直方图;
2)检验分布的正态性;
3)若检验符合正态分布,估计正态分布的参数并检验参数.
(2)据说某地汽油的价格是每加仑115美分,为了验证这种说法,一位学者开车随机选择了一些加油站,得到某年一月和二月的数据如下:
一月:119 117 115 116 112 121 115 122 116 118 109 112 119 112 117 113 114 109 109 118
二月:118 119 115 122 118 121 120 122 128 116 120 123 121 119 117 119 128 126 118 125
1)分别用两个月的数据验证这种说法的可靠性;
2)分别给出1月和2月汽油价格的置信区间;
3)给出1月和2月汽油价格差的置信区间.
实验步骤
1、解:主要使用MATLAB与SPSS求解,具体求解步骤如下,
(1)编写MATLAB程序求解,代码如下

1 %数据 2 x=[93,75,83,93,91,85,84,82,77,76,77,95,94,89,91,88,86,83,96,81,79,97,78,75,67,69,68,84,83,81,75,66,85,70,94,84,83,82,80,78,74,73,76,70,86,76,90,89,71,66,86,73,80,94,79,78,77,63,53,55]; 3 %总样本数 4 n=length(x); 5 %平均值 6 x_bar=sum(x)*1/n 7 %标准差 8 temp1=0; 9 for i=1:n 10 c=x(i)-x_bar; 11 temp1=temp1+c^2; 12 end 13 s=sqrt(temp1*(1/(n-1))) 14 %极差 15 x_max=max(x); 16 x_min=min(x); 17 x_jicha=x_max-x_min 18 %偏度 19 temp2=0; 20 for i=1:n 21 c=x(i)-x_bar; 22 temp2=temp2+c^3; 23 end 24 g1=(1/s)^3*temp2 25 %峰度 26 temp3=0; 27 for i=1:n 28 c=x(i)-x_bar; 29 temp3=temp3+c^4; 30 end 31 g2=(1/s)^4*temp3 32 %画出直方图 33 bar(x)
运行结果,
|
平均值 |
标准差 |
极差 |
偏度 |
峰度 |
|
80.10 |
9.71 |
44.00 |
-27.39 |
1.83 |
见图
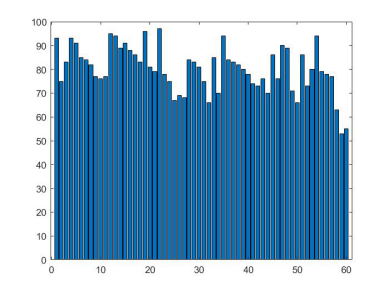
(2)SPSS求解步骤:
首先,做出正态曲线直方图:
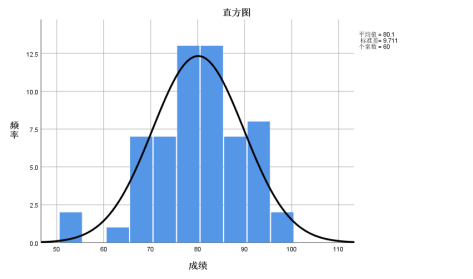
由上图可见,该校这60名学生的的成绩分布与正态分布相近。本报告对其做正态检验。
画出Q-Q图和P-P图
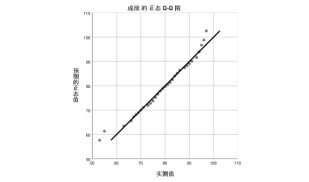
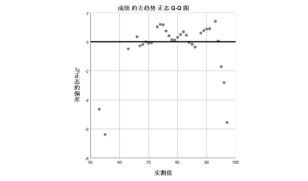
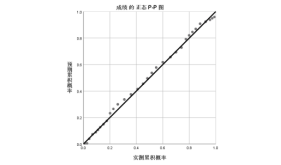
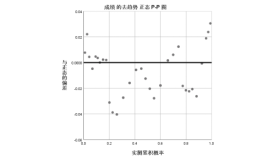
由上所做图像可知,数据序列稍有偏差地集中在直线上,并由去趋势的正态P-P
由图可见,数据点的偏差均小于0.04,可以认为该60名学生的成绩符合正态分布。下面对此做进一步检验。使用K-S检验
|
单样本柯尔莫戈洛夫-斯米诺夫检验 |
||
|
|
成绩 |
|
|
个案数 |
60 |
|
|
正态参数a,b |
平均值 |
80.10 |
|
标准 偏差 |
9.711 |
|
|
最极端差值 |
绝对 |
.066 |
|
正 |
.041 |
|
|
负 |
-.066 |
|
|
检验统计 |
.066 |
|
|
渐近显著性(双尾) |
.200c,d |
|
|
a. 检验分布为正态分布。 |
||
|
b. 根据数据计算。 |
||
|
c. 里利氏显著性修正。 |
||
|
d. 这是真显著性的下限。 |
||
综上所述,该校60名学生的成绩符合正态分布。
(3)由(2)可知,该60名学生的成绩符合正态分布。对正态分布的均值和方差的最大似然估计分别为,
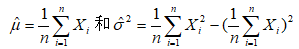
使用MATLAB求解,代码如下

1 %估计均值 2 niu=x_bar 3 %估计方差 4 temp4=0; 5 d=1/n; 6 for i=1:n 7 c=x(i)^2; 8 temp4=temp4+c; 9 end 10 sigama=d*temp4-(d*sum(x))^2

使用SPSS对估计值进行检验,首先对均值进行t检验。
|
单样本统计 |
||||
|
|
个案数 |
平均值 |
标准 偏差 |
标准 误差平均值 |
|
成绩 |
60 |
80.10 |
9.711 |
1.254 |
|
单样本检验 |
||||||
|
|
检验值 = 80.1 |
|||||
|
t |
自由度 |
Sig.(双尾) |
平均值差值 |
差值 95% 置信区间 |
||
|
下限 |
上限 |
|||||
|
成绩 |
.000 |
59 |
1.000 |
.000 |
-2.51 |
2.51 |

2、解:主要使用MATLAB求解,
(1) 首先使用一月份的数据检验该说法,对该组数据进行t检验,零假设为可靠,非零假设为不可靠,代码如下

1 %一月份的 2 x1=[119,117,115,116,112,121,115,122,116,118,109,112,119,112,117,113,114,109,109,118]; 3 [h,sig,ci]=ttest(x1,115)
一月份t检验的结论
|
h |
sig |
ci |
|
0 |
0.8642 |
113.34~116.96 |

1 %二月份的 2 x2=[118,119,115,122,118,121,120,122,128,116,120,123,121,119,117,119,128,126,118,125]; 3 [h,sig,ci]=ttest(x2,115)
二月份t的检验的结论,
|
h |
sig |
ci |
|
1 |
1.32e-6 |
119.01~122.49 |
由上述的计算结果,得到如下结论,在一月份该说法是合理的,在二月份该说法是不合理的。
(1) 分别给出1月和2月汽油价格的置信区间α=0.05;
一月份汽油价格的置信区间,使用MATLAB求解:

1 %一月份的 2 x1=[119,117,115,116,112,121,115,122,116,118,109,112,119,112,117,113,114,109,109,118]; 3 [mu1,sigmal,mucil,sigmacil]=normfit(x1,0.05)
计算结果主要展示置信区间,(113.3388,116.9612)。
二月份汽油价格的置信区间,使用MATLAB求解:

1 %二月份的 2 x2=[118,119,115,122,118,121,120,122,128,116,120,123,121,119,117,119,128,126,118,125]; 3 [mu2,sigma2,muci2,sigmaci2]=normfit(x2,0.05)
计算结果主要展示置信区间,(119.0129,122.4871)。
(1) 给出1月和2月汽油价格差的置信区间,使用MATLAB求解:

1 x1=[119,117,115,116,112,121,115,122,116,118,109,112,119,112,117,113,114,109,109,118]; 2 x2=[118,119,115,122,118,121,120,122,128,116,120,123,121,119,117,119,128,126,118,125]; 3 [h1,sig1,ci1]=normfit(x2-x1,0.05) 4 [h2,sig2,ci2]=ttest(x2,x1,0.05,0)
计算结果:
|
月份 |
h |
sig |
ci |
|
1 |
5.6000 |
5.4715 |
3.0393~8.1607 |
|
2 |
1.0000 |
2.0582e-04 |
3.0393~8.1607 |
结果如上表所示。
小结
在做统计分析的过程中,SPSS的体验最友好,但是使用SPSS并不能很好地体会到每一步的计算算结果的由来,在学习统计学的初期建议使用MATLAB或者SPSS编程求解统计学问题。



