SPSS的Logistics回归
实验目的
学会使用SPSS的简单操作,Logistic回归。
实验要求
使用SPSS。
实验内容

实验步骤
(1)二项分类Logistic回归SPSS分析,使用Hosmer和Lemeshow于1989年研究低出生体重婴儿的影响因素作为演示例子。结果变量为“是否娩出低出生体重儿”,考虑影响因素有8个,详见Logistics_step.sav文件。本例题主要演示“自变量的筛选与逐步回归”。操作如下:点击【分析】→【回归】→【二元Logistics回归】,在打开的对话框中,把待结果变量LOW选入【因变量】中,将变量LWT,AGE,SMOKE,PTL,HT,UI,FTV,RACE选入【协变量】中。点击【分类】,把RACE选入【分类协变量】→【第一个】→【变化量】→【继续】,【块】里的【方法(M)】选【向前:LP】,【选项】→【Exp(B)的置信区间】→【继续】,单击【运行】。

主要分析结果如下:
|
分类变量编码 |
||||
|
|
频率 |
参数编码 |
||
|
(1) |
(2) |
|||
|
种族 |
白人 |
96 |
.000 |
.000 |
|
黑人 |
26 |
1.000 |
.000 |
|
|
其他种族 |
67 |
.000 |
1.000 |
|
上表输出race在产生哑变量时的编码情况,以白人为参照水平。
|
未包括在方程中的变量 |
|||||
|
|
得分 |
自由度 |
显著性 |
||
|
步骤 0 |
变量 |
产妇体重 |
4.616 |
1 |
.032 |
|
产妇年龄 |
2.407 |
1 |
.121 |
||
|
产妇在妊娠期间是否吸烟 |
4.924 |
1 |
.026 |
||
|
本次妊娠前早产次数 |
7.267 |
1 |
.007 |
||
|
是否患有高血压 |
4.388 |
1 |
.036 |
||
|
应激性 |
4.205 |
1 |
.040 |
||
|
随访次数 |
.934 |
1 |
.334 |
||
|
种族 |
5.005 |
2 |
.082 |
||
|
种族(1) |
1.727 |
1 |
.189 |
||
|
种族(2) |
1.797 |
1 |
.180 |
||
|
总体统计 |
29.140 |
9 |
.001 |
||
输出的是拟合包含常数项和任一自变量的Logistics回归模型检验统计量、自由度及P值。其中race产生两个哑变量,因此其总自由度为2。由上表可以发现,本次妊娠前早产次数(ptl)的score统计量最大,P=0.007,小于SPSS默认选入变量的标准(0.05)因此下一步将它首先选入模型。
|
模型系数的 Omnibus 检验 |
||||
|
|
卡方 |
自由度 |
显著性 |
|
|
步骤 1 |
步骤 |
6.779 |
1 |
.009 |
|
块 |
6.779 |
1 |
.009 |
|
|
模型 |
6.779 |
1 |
.009 |
|
|
步骤 2 |
步骤 |
4.309 |
1 |
.038 |
|
块 |
11.089 |
2 |
.004 |
|
|
模型 |
11.089 |
2 |
.004 |
|
|
步骤 3 |
步骤 |
6.363 |
1 |
.012 |
|
块 |
17.452 |
3 |
.001 |
|
|
模型 |
17.452 |
3 |
.001 |
|
输出了对每一步引入变量后,对模型中是否所有参数均为0的似然比检验。
|
模型摘要 |
|||
|
步骤 |
-2 对数似然 |
考克斯-斯奈尔 R 方 |
内戈尔科 R 方 |
|
1 |
227.893a |
.035 |
.050 |
|
2 |
223.583b |
.057 |
.080 |
|
3 |
217.220b |
.088 |
.124 |
|
a. 由于参数估算值的变化不足 .001,因此估算在第 3 次迭代时终止。 |
|||
|
b. 由于参数估算值的变化不足 .001,因此估算在第 4 次迭代时终止。 |
|||
输出每一步时的-2log(L),可用于进行似然比检验,还输出两种伪决定系数。
|
方程中的变量 |
|||||||||
|
|
B |
标准误差 |
瓦尔德 |
自由度 |
显著性 |
Exp(B) |
EXP(B) 的 95% 置信区间 |
||
|
下限 |
上限 |
||||||||
|
步骤 1a |
本次妊娠前早产次数 |
.802 |
.317 |
6.391 |
1 |
.011 |
2.230 |
1.197 |
4.151 |
|
常量 |
-.964 |
.175 |
30.370 |
1 |
.000 |
.381 |
|
|
|
|
步骤 2b |
本次妊娠前早产次数 |
.823 |
.318 |
6.683 |
1 |
.010 |
2.277 |
1.220 |
4.250 |
|
是否患有高血压 |
1.272 |
.616 |
4.270 |
1 |
.039 |
3.569 |
1.068 |
11.930 |
|
|
常量 |
-1.062 |
.184 |
33.224 |
1 |
.000 |
.346 |
|
|
|
|
步骤 3c |
产妇体重 |
-.015 |
.007 |
5.584 |
1 |
.018 |
.985 |
.972 |
.997 |
|
本次妊娠前早产次数 |
.728 |
.327 |
4.961 |
1 |
.026 |
2.071 |
1.091 |
3.929 |
|
|
是否患有高血压 |
1.789 |
.694 |
6.639 |
1 |
.010 |
5.986 |
1.535 |
23.348 |
|
|
常量 |
.893 |
.829 |
1.158 |
1 |
.282 |
2.441 |
|
|
|
|
a. 在步骤 1 输入的变量:本次妊娠前早产次数。 |
|||||||||
|
b. 在步骤 2 输入的变量:是否患有高血压。 |
|||||||||
|
c. 在步骤 3 输入的变量:产妇体重。 |
|||||||||
输出了每一步逐步回归得到的模型中参数估计及其标准误、Waldχ2等。另外还输出了OR值95%的可信区间。
|
模型(如果除去项) |
|||||
|
变量 |
模型对数似然 |
-2 对数似然的变化 |
自由度 |
变化量的显著性 |
|
|
步骤 1 |
本次妊娠前早产次数 |
-117.336 |
6.779 |
1 |
.009 |
|
步骤 2 |
本次妊娠前早产次数 |
-115.325 |
7.067 |
1 |
.008 |
|
是否患有高血压 |
-113.946 |
4.309 |
1 |
.038 |
|
|
步骤 3 |
产妇体重 |
-111.792 |
6.363 |
1 |
.012 |
|
本次妊娠前早产次数 |
-111.231 |
5.242 |
1 |
.022 |
|
|
是否患有高血压 |
-112.145 |
7.070 |
1 |
.008 |
|
输出了对于已在模型中的自变量是否需要被剔除出模型的似然比检验结果,结论是“一个不能少”。
|
未包括在方程中的变量 |
|||||
|
|
得分 |
自由度 |
显著性 |
||
|
步骤 1 |
变量 |
产妇体重 |
3.340 |
1 |
.068 |
|
产妇年龄 |
3.149 |
1 |
.076 |
||
|
产妇在妊娠期间是否吸烟 |
3.164 |
1 |
.075 |
||
|
是否患有高血压 |
4.722 |
1 |
.030 |
||
|
应激性 |
2.162 |
1 |
.141 |
||
|
随访次数 |
.753 |
1 |
.385 |
||
|
种族 |
5.359 |
2 |
.069 |
||
|
种族(1) |
2.056 |
1 |
.152 |
||
|
种族(2) |
1.712 |
1 |
.191 |
||
|
总体统计 |
22.858 |
8 |
.004 |
||
|
步骤 2 |
变量 |
产妇体重 |
5.830 |
1 |
.016 |
|
产妇年龄 |
3.108 |
1 |
.078 |
||
|
产妇在妊娠期间是否吸烟 |
3.117 |
1 |
.078 |
||
|
应激性 |
3.010 |
1 |
.083 |
||
|
随访次数 |
.520 |
1 |
.471 |
||
|
种族 |
4.882 |
2 |
.087 |
||
|
种族(1) |
1.597 |
1 |
.206 |
||
|
种族(2) |
1.834 |
1 |
.176 |
||
|
总体统计 |
18.690 |
7 |
.009 |
||
|
步骤 3 |
变量 |
产妇年龄 |
1.725 |
1 |
.189 |
|
产妇在妊娠期间是否吸烟 |
2.821 |
1 |
.093 |
||
|
应激性 |
2.236 |
1 |
.135 |
||
|
随访次数 |
.236 |
1 |
.627 |
||
|
种族 |
5.216 |
2 |
.074 |
||
|
种族(1) |
3.477 |
1 |
.062 |
||
|
种族(2) |
.605 |
1 |
.437 |
||
|
总体统计 |
13.360 |
6 |
.038 |
||
输出了尚不在模型中是否能被引入的score检验结果,结论是在第二步引入“是否患有高血压(ht)”。
逐步回归结果对于当前样本数据集效果较好,但对于相同研究的另一个数据库应用同样的逐步回归方法不能得到同样的自变量子集。尤其对于样本含量较小的数据库,结果更不稳定。
|
分类表a |
|||||||||||
|
|
实测 |
预测 |
|||||||||
|
|
低出生体重儿 |
正确百分比 |
|||||||||
|
|
正常 |
低出生体重 |
|||||||||
|
步骤 1 |
低出生体重儿 |
正常 |
126 |
4 |
96.9 |
||||||
|
低出生体重 |
57 |
2 |
3.4 |
||||||||
|
总体百分比 |
|
|
67.7 |
||||||||
|
步骤 2 |
低出生体重儿 |
正常 |
121 |
9 |
93.1 |
||||||
|
低出生体重 |
50 |
9 |
15.3 |
||||||||
|
总体百分比 |
|
|
68.8 |
||||||||
|
步骤 3 |
低出生体重儿 |
正常 |
123 |
7 |
94.6 |
||||||
|
低出生体重 |
47 |
12 |
20.3 |
||||||||
|
总体百分比 |
|
|
71.4 |
||||||||
|
a. 分界值为 .500 |
|||||||||||
由上表可以看出,预测正确的记录占样本的全部记录的71.4%,其中出生体重正常者中有94.6%的人被预测为正常,但低出生体重中只有20.3%的人被预测粗低出生体重。
应用ROC曲线确定合理到预测概率分类点,即将预测概率大于(或小于)多少的研究对象判断为阳性结果(或阴性结果)。SPSS操作,先得到Logistics得到的预测的分类结果和概率,
在Logistics回归的对话框中,【保存】→【预测值】→【概率】→【组成员】→【继续】。

1 LOGISTIC REGRESSION VARIABLES low 2 /METHOD=FSTEP(LR) lwt age smoke ptl ht ui ftv race 3 /CONTRAST (race)=Indicator(1) 4 /SAVE=PRED PGROUP 5 /PRINT=CI(95) 6 /CRITERIA=PIN(0.05) POUT(0.10) ITERATE(20) CUT(0.5).
ROC曲线的SPSS操作,【分析】→【ROC曲线】,在对话框中把PRE_1选入【检验变量】,把low选入【状态变量】,【状态变量值】为设为1,【显示】勾选“ROC曲线”、“带对角参考线”和“标准误差和置信区间”,单击【确定】。
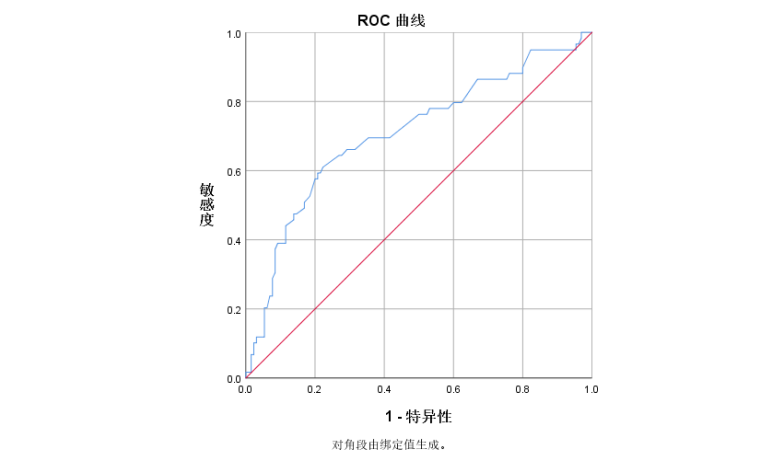
上图便是ROC曲线,预测效果最佳时,曲线应该是从左下角垂直上升至顶,然后水平方向向后延伸到右上角。如果ROC曲线沿着主对角线方向分布,表示分类是机遇造成的,正确分类和错分到概率各位50%,此时该诊断方法完全无效。从上图可见,当前模型有一些效果。
|
曲线下方的区域 |
||||
|
检验结果变量: 预测概率 |
||||
|
区域 |
标准 错误a |
渐近显著性b |
渐近 95% 置信区间 |
|
|
下限 |
上限 |
|||
|
.708 |
.043 |
.000 |
.624 |
.792 |
|
检验结果变量 预测概率 至少有一个在正实际状态组与负实际状态组之间的绑定值。统计可能有偏差。 |
||||
|
a. 按非参数假定 |
||||
|
b. 原假设:真区域 = 0.5 |
||||
上表为对曲线下面积进行计算的结果,给出了曲线下面积的估计值和标准误差,可见如果根据当前模型预测概率进行预测,则ROC曲线下面积为0.708,其95%可信区间为(0.624~0.792)。随后进行的是面积是否为0.5的检验P值和95%克新鲜。浇筑表明用的是非参数假设,无效假设是面积为0.5、可见当前模型的预测效果和无效模型比起来还是有差异的。

1 ROC PRE_1 BY low (1) 2 /PLOT=CURVE(REFERENCE) 3 /PRINT=SE 4 /CRITERIA=CUTOFF(INCLUDE) TESTPOS(LARGE) DISTRIBUTION(FREE) CI(95) 5 /MISSING=EXCLUDE.
拟合优度检验,在【Logistics回归】的对话框中,【选项】,勾选【霍斯默-莱梅肖拟合优度检验】。
|
霍斯默-莱梅肖检验的列联表 |
||||||
|
|
低出生体重儿 = 正常 |
低出生体重儿 = 低出生体重 |
总计 |
|||
|
实测 |
期望 |
实测 |
期望 |
|||
|
步骤 1 |
1 |
118 |
115.110 |
41 |
43.890 |
159 |
|
2 |
12 |
14.890 |
18 |
15.110 |
30 |
|
|
步骤 2 |
1 |
113 |
110.708 |
36 |
38.292 |
149 |
|
2 |
8 |
12.306 |
14 |
9.694 |
22 |
|
|
3 |
9 |
6.986 |
9 |
11.014 |
18 |
|
|
步骤 3 |
1 |
16 |
16.697 |
3 |
2.303 |
19 |
|
2 |
15 |
15.303 |
4 |
3.697 |
19 |
|
|
3 |
18 |
17.461 |
5 |
5.539 |
23 |
|
|
4 |
16 |
13.215 |
2 |
4.785 |
18 |
|
|
5 |
15 |
13.708 |
4 |
5.292 |
19 |
|
|
6 |
15 |
12.683 |
3 |
5.317 |
18 |
|
|
7 |
11 |
12.310 |
7 |
5.690 |
18 |
|
|
8 |
11 |
12.279 |
8 |
6.721 |
19 |
|
|
9 |
6 |
10.531 |
13 |
8.469 |
19 |
|
|
10 |
7 |
5.812 |
10 |
11.188 |
17 |
|

1 LOGISTIC REGRESSION VARIABLES low 2 /METHOD=FSTEP(LR) lwt age smoke ptl ht ui ftv race 3 /CONTRAST (race)=Indicator(1) 4 /SAVE=PRED PGROUP 5 /PRINT=GOODFIT CI(95) 6 /CRITERIA=PIN(0.05) POUT(0.10) ITERATE(20) CUT(0.5).
(2)有条件Logistic回归SPSS操作,分析示例——Mack等人考察服用雌激素与患子宫内膜癌的关系,对退休住在社区的妇女进行调查,详见1_1_Logistics.sav文件。点击【分析】→【回归】→【多元Logistics】,把case选入【因变量】,把age,est,gall,nonest选入【协变量】。【模型】去掉【在模型中包括截距】→【继续】。单击【确定】。

|
模型拟合信息 |
||||
|
模型 |
模型拟合条件 |
似然比检验 |
||
|
-2 对数似然 |
卡方 |
自由度 |
显著性 |
|
|
空 |
87.337 |
|
|
|
|
最终 |
53.178 |
34.159 |
4 |
.000 |
似然比检验,不全为0。
|
伪 R 方 |
|
|
考克斯-斯奈尔 |
.419 |
|
内戈尔科 |
.558 |
|
麦克法登 |
.391 |
本例的伪决定系数比较大。
|
似然比检验 |
||||
|
效应 |
模型拟合条件 |
似然比检验 |
||
|
简化模型的 -2 对数似然 |
卡方 |
自由度 |
显著性 |
|
|
age |
53.658 |
.480 |
1 |
.488 |
|
est |
72.013 |
18.836 |
1 |
.000 |
|
gall |
58.770 |
5.592 |
1 |
.018 |
|
nonest |
53.279 |
.102 |
1 |
.750 |
|
卡方统计是最终模型与简化模型之间的 -2 对数似然之差。简化模型是通过在最终模型中省略某个效应而形成。原假设是,该效应的所有参数均为 0。 |
||||
输出从当前模型中分别剔除每一个自变量后拟合新的条件Logistics回归模型的负2倍似然对数值,用于考察是否可以从当前模型中剔除该自变量。可以看出年龄、gall和nonest的P值均大于0.05.提示可以进一步采用逐步回归法对当前模型中自变量进行筛选。
|
参数估算值 |
|||||||||
|
case |
B |
标准 错误 |
瓦尔德 |
自由度 |
显著性 |
Exp(B) |
Exp(B) 的 95% 置信区间 |
||
|
下限 |
上限 |
||||||||
|
1.00 |
age |
.277 |
.403 |
.473 |
1 |
.491 |
1.320 |
.599 |
2.908 |
|
est |
2.698 |
.824 |
10.712 |
1 |
.001 |
14.851 |
2.952 |
74.723 |
|
|
gall |
1.836 |
.904 |
4.122 |
1 |
.042 |
6.270 |
1.066 |
36.893 |
|
|
nonest |
.256 |
.807 |
.100 |
1 |
.752 |
1.291 |
.265 |
6.279 |
|
由上表可见,服用雌激素患者子宫内膜癌的概率时未服用雌激素的14.851倍。有胆囊病史患者患子宫癌的概率是没有胆囊史者的6.270倍,但P=0.042,下这一结论要小心谨慎,可以适当扩大样本量,在对这一因素进行研究。这里的P值与上面的P值并不相同,是因为此处使用的是Wald统计量。

1 NOMREG case (BASE=LAST ORDER=ASCENDING) WITH age est gall nonest 2 /CRITERIA CIN(95) DELTA(0) MXITER(100) MXSTEP(5) CHKSEP(20) LCONVERGE(0) PCONVERGE(0.000001) 3 SINGULAR(0.00000001) 4 /MODEL 5 /STEPWISE=PIN(.05) POUT(0.1) MINEFFECT(0) RULE(SINGLE) ENTRYMETHOD(LR) REMOVALMETHOD(LR) 6 /INTERCEPT=EXCLUDE 7 /PRINT=PARAMETER SUMMARY LRT CPS STEP MFI.
(2)有序Logistics回归SPSS分析,分析示例——对某地人群调查其对所从事的工作是否满意,可能的影响因素有年龄、性别、年收入水平、文化程度。数据详见satisfy.sav文件。SPSS操作,点击【分析】→【回归】→【有序】,把satis选入【因变量】,把inccat,edu,gender选入【因子】,把age选入【协变量】。单击【确定】。
|
模型拟合信息 |
||||
|
模型 |
-2 对数似然 |
卡方 |
自由度 |
显著性 |
|
仅截距 |
7297.880 |
|
|
|
|
最终 |
6202.150 |
1095.730 |
9 |
.000 |
|
关联函数:分对数。 |
||||
上表是对模型中是否所有自变量偏回归系数全为0进行似然比检验,结果P<0.001,说明至少有一个自变量的偏回归系数不为0。换句话说,拟合包括年龄、性别、收入、文化程度4个自变量的模型拟合优度好于仅包含常数项的模型。
|
拟合优度 |
|||
|
|
卡方 |
自由度 |
显著性 |
|
皮尔逊 |
3105.220 |
3049 |
.235 |
|
偏差 |
3501.627 |
3049 |
.000 |
|
关联函数:分对数。 |
|||
输出的是Pearson和Deviance两种拟合优度检验结果。但这两个统计量有个致命的缺点是对于自变量取值水平组合的实际观察频数为0的比例十分敏感,如果上述比例过高,这两个统计量不一定人就服从χ2分布,因而基于χ2分布计算的P值也不可信。也就是说,这两个统计量不一定能真实地反映模型拟合情况。当自变量中存在连续性变量时,如本例中的年龄,常会导致上述比例过高。与上述的两个统计量相比,似然比χ2则要稳健得多。本例两个统计量对应的P值均小于0.05.
|
伪 R 方 |
|
|
考克斯-斯奈尔 |
.157 |
|
内戈尔科 |
.179 |
|
麦克法登 |
.080 |
|
关联函数:分对数。 |
|
输出了三种伪决定系数。
|
参数估算值 |
||||||||
|
|
估算 |
标准 错误 |
瓦尔德 |
自由度 |
显著性 |
95% 置信区间 |
||
|
下限 |
上限 |
|||||||
|
阈值 |
[satis = 1] |
-1.288 |
.150 |
73.282 |
1 |
.000 |
-1.583 |
-.993 |
|
[satis = 2] |
-.263 |
.150 |
3.098 |
1 |
.078 |
-.557 |
.030 |
|
|
位置 |
age |
-.031 |
.002 |
199.377 |
1 |
.000 |
-.035 |
-.026 |
|
[inccat=1] |
1.618 |
.081 |
402.390 |
1 |
.000 |
1.460 |
1.776 |
|
|
[inccat=2] |
1.071 |
.067 |
257.308 |
1 |
.000 |
.940 |
1.202 |
|
|
[inccat=3] |
.607 |
.076 |
63.401 |
1 |
.000 |
.457 |
.756 |
|
|
[inccat=4] |
0a |
. |
. |
0 |
. |
. |
. |
|
|
[edu=1] |
-.772 |
.116 |
44.233 |
1 |
.000 |
-1.000 |
-.545 |
|
|
[edu=2] |
-.510 |
.111 |
20.914 |
1 |
.000 |
-.728 |
-.291 |
|
|
[edu=3] |
-.312 |
.115 |
7.395 |
1 |
.007 |
-.537 |
-.087 |
|
|
[edu=4] |
-.096 |
.115 |
.696 |
1 |
.404 |
-.320 |
.129 |
|
|
[edu=5] |
0a |
. |
. |
0 |
. |
. |
. |
|
|
[gender=f] |
.045 |
.049 |
.855 |
1 |
.355 |
-.050 |
.140 |
|
|
[gender=m] |
0a |
. |
. |
0 |
. |
. |
. |
|
|
关联函数:分对数。 |
||||||||
|
a. 此参数冗余,因此设置为零。 |
||||||||
输出了最重要的结果:回归系数估计。本例反应变量水平为3,因此会建立两个回归方程,固有两个常数项。建立如下模型:

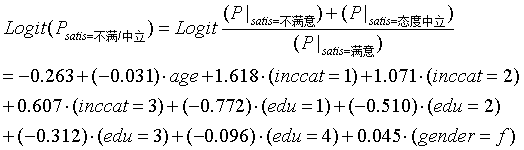
代码:

1 PLUM satis BY inccat edu gender WITH age 2 /CRITERIA=CIN(95) DELTA(0) LCONVERGE(0) MXITER(100) MXSTEP(5) PCONVERGE(1.0E-6) SINGULAR(1.0E-8) 3 /LINK=LOGIT 4 /PRINT=FIT PARAMETER SUMMARY.
模型使用条件检验,具体用【输出】的子对话框,勾选【平行线检验】。
|
平行线检验a |
||||
|
模型 |
-2 对数似然 |
卡方 |
自由度 |
显著性 |
|
原假设 |
6202.150 |
|
|
|
|
常规 |
6189.793 |
12.357 |
9 |
.194 |
|
原假设指出,位置参数(斜率系数)在各个响应类别中相同。 |
||||
|
a. 关联函数:分对数。 |
||||
输出的是检验个自变量对于反应变量的影响在两个回归方程中是否相同结果。如果P>0.05,说明各回归方程互相平行,可以使用有序Logistics回归过程进行分析。
作图SPSS操作,见代码,

1 GRAPH 2 /LINE(MULTIPLE)=MEAN(EST1_1) MEAN(EST2_1) MEAN(EST3_1) BY age 3 /MISSING=LISTWISE.
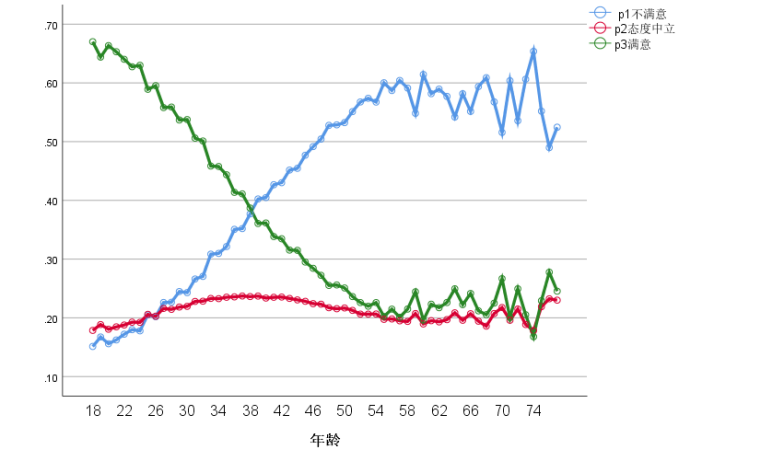

1 GRAPH 2 /LINE(MULTIPLE)=MEAN(logitp1) MEAN(logitp2) BY age 3 /MISSING=LISTWISE.

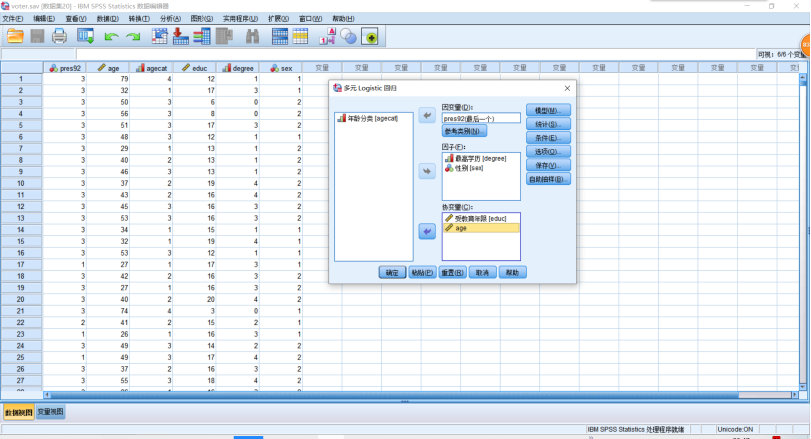
(4)多项分类Logistics回归SPSS分析,实例——回顾老布什与克林顿在1992年进行的较量,数据来自SPSS自带的vote.sav,详见该文件,试对其拟合反应变量为无序多分类的Logistics回归,看看哪些因素导致了老布什的败北,希望特朗普能从中吸取教训。点击【分析】→【回归】→【多元Logistics】,把pres92选入【因变量】,把degree,sex选入【因子】,把age,educ选入【协变量】。单击【确定】。
|
模型拟合信息 |
||||
|
模型 |
模型拟合条件 |
似然比检验 |
||
|
-2 对数似然 |
卡方 |
自由度 |
显著性 |
|
|
仅截距 |
2718.636 |
|
|
|
|
最终 |
2600.138 |
118.497 |
14 |
.000 |
输出了反应变量与离散自变量不同取值水平的边际频数分布。
|
模型拟合信息 |
||||
|
模型 |
模型拟合条件 |
似然比检验 |
||
|
-2 对数似然 |
卡方 |
自由度 |
显著性 |
|
|
仅截距 |
2718.636 |
|
|
|
|
最终 |
2600.138 |
118.497 |
14 |
.000 |
对模型中是否所有自变量偏回归系数全为0进行似然比检验。表中表明至少有一个自变量的偏回归系数不为0.
|
伪 R 方 |
|
|
考克斯-斯奈尔 |
.062 |
|
内戈尔科 |
.072 |
|
麦克法登 |
.032 |
拟合模型:
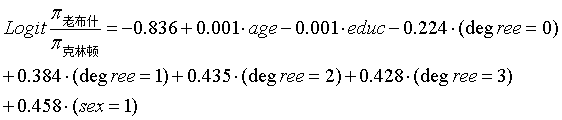
|
似然比检验 |
||||
|
效应 |
模型拟合条件 |
似然比检验 |
||
|
简化模型的 -2 对数似然 |
卡方 |
自由度 |
显著性 |
|
|
截距 |
2600.138a |
.000 |
0 |
. |
|
受教育年限 |
2600.141 |
.003 |
2 |
.999 |
|
age |
2641.003 |
40.865 |
2 |
.000 |
|
最高学历 |
2627.453 |
27.314 |
8 |
.001 |
|
性别 |
2637.480 |
37.341 |
2 |
.000 |
|
卡方统计是最终模型与简化模型之间的 -2 对数似然之差。简化模型是通过在最终模型中省略某个效应而形成。原假设是,该效应的所有参数均为 0。 |
||||
|
a. 因为省略此效应并不会增加自由度,所以此简化模型相当于最终模型。 |
||||
|
参数估算值 |
|||||||||
|
候选人a |
B |
标准 错误 |
瓦尔德 |
自由度 |
显著性 |
Exp(B) |
Exp(B) 的 95% 置信区间 |
||
|
下限 |
上限 |
||||||||
|
Bush |
截距 |
-.836 |
.778 |
1.156 |
1 |
.282 |
|
|
|
|
受教育年限 |
-.001 |
.039 |
.001 |
1 |
.978 |
.999 |
.925 |
1.079 |
|
|
age |
.001 |
.003 |
.096 |
1 |
.757 |
1.001 |
.994 |
1.008 |
|
|
[最高学历=0] |
-.224 |
.426 |
.277 |
1 |
.599 |
.799 |
.347 |
1.841 |
|
|
[最高学历=1] |
.384 |
.283 |
1.845 |
1 |
.174 |
1.468 |
.843 |
2.556 |
|
|
[最高学历=2] |
.435 |
.298 |
2.133 |
1 |
.144 |
1.545 |
.862 |
2.771 |
|
|
[最高学历=3] |
.428 |
.213 |
4.057 |
1 |
.044 |
1.534 |
1.012 |
2.328 |
|
|
[最高学历=4] |
0b |
. |
. |
0 |
. |
. |
. |
. |
|
|
[性别=1] |
.458 |
.105 |
19.040 |
1 |
.000 |
1.580 |
1.287 |
1.941 |
|
|
[性别=2] |
0b |
. |
. |
0 |
. |
. |
. |
. |
|
|
Perot |
截距 |
-.759 |
1.105 |
.472 |
1 |
.492 |
|
|
|
|
受教育年限 |
-.003 |
.055 |
.003 |
1 |
.959 |
.997 |
.894 |
1.112 |
|
|
age |
-.030 |
.005 |
33.000 |
1 |
.000 |
.971 |
.961 |
.981 |
|
|
[最高学历=0] |
-.259 |
.641 |
.164 |
1 |
.685 |
.771 |
.220 |
2.708 |
|
|
[最高学历=1] |
.770 |
.411 |
3.512 |
1 |
.061 |
2.160 |
.965 |
4.835 |
|
|
[最高学历=2] |
.853 |
.411 |
4.301 |
1 |
.038 |
2.347 |
1.048 |
5.256 |
|
|
[最高学历=3] |
.618 |
.316 |
3.819 |
1 |
.051 |
1.856 |
.998 |
3.450 |
|
|
[最高学历=4] |
0b |
. |
. |
0 |
. |
. |
. |
. |
|
|
[性别=1] |
.772 |
.142 |
29.469 |
1 |
.000 |
2.165 |
1.638 |
2.861 |
|
|
[性别=2] |
0b |
. |
. |
0 |
. |
. |
. |
. |
|
|
a. 参考类别为:^1。 |
|||||||||
|
b. 此参数冗余,因此设置为零。 |
|||||||||
由所建立的模型可以看出:别的自变量没有统计学意义,只有选民的性别有统计学意义,选民性别的偏回归系数为0.458,OR值为1.58,这说明男性选民选老布什的概率与选克林顿的概率之比,较女性选民的这一比值大1.58倍。
代码:

1 NOMREG pres92 (BASE=LAST ORDER=ASCENDING) BY degree sex WITH educ age 2 /CRITERIA CIN(95) DELTA(0) MXITER(100) MXSTEP(5) CHKSEP(20) LCONVERGE(0) PCONVERGE(0.000001) 3 SINGULAR(0.00000001) 4 /MODEL 5 /STEPWISE=PIN(.05) POUT(0.1) MINEFFECT(0) RULE(SINGLE) ENTRYMETHOD(LR) REMOVALMETHOD(LR) 6 /INTERCEPT=INCLUDE 7 /PRINT=PARAMETER SUMMARY LRT CPS STEP MFI.
小结
二分类logistics对资料的要求:
(1)反应变量为二分类的分类变量或是某事件的发生率(由于流行病学中的发病率存在一个研究对象重复计数的现象,不适用于Logistics回归,反应变量不服从二项分布)。
(2)自变量与logit(P)之间为线性关系。
(3)残差合计为0,且服从二项分布。
(4)各观察量相互独立。
在SPSS中应用多元Logistics过程处理配对Logistics回归时,需注意:
(1)数据库结构与应用Cox过程不同。此处的数据库中每一条记录包括一个对子中的两个观察对象。
(2)所拟合的模型不能包含常数项。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号