Matlab最短路问题
实验目的
掌握动态规划算法和最短路径求法,利用最短路径知识结合实际问题建立数学模型。
实验要求
实验步骤要有模型建立,模型求解、结果分析。
实验内容
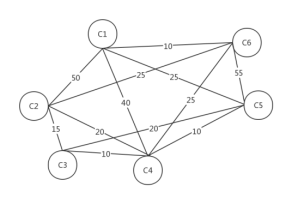
(1)某公司在六个城市C1,C2,C3,C4,C5,C6中都有分公司,从Ci到Cj的直达航班票价由下述矩阵的第i行、第j列元素给出(∞表示无直达航班),该公司想算出一张任意两个城市之间最廉价路线表,试作出这样的表来
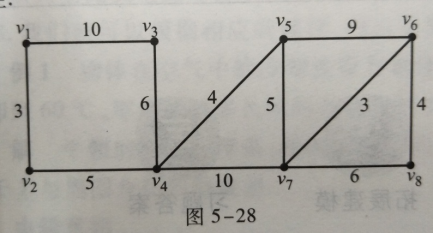
 (2)求图5-28中每一结点到其他结点的最短路
(2)求图5-28中每一结点到其他结点的最短路
(3)一只狼、一只羊和一筐白菜在河的一岸,一个摆渡人想把它们渡过河去,但是由于他的船很小,每次只能带走它们之中的一样,由于明显的原因,狼和羊或者羊和白菜在一起需要人看守,问摆渡人怎样把它们渡过河去?
实验步骤
(1)解:该公司想算出一张任意两个城市之间最廉价路线表,可把这个路线表抽象成一副带权的无向图,于是问题等价于求每对顶点之间最短的问题。本题使用Floyd算法,用MATLAB编程求解
 首先,编写floyd.m文件,代码如下,
首先,编写floyd.m文件,代码如下,

1 %Floyd算法——每对顶点间的最短路径算法 2 %输入:带权邻接矩阵w(i,j). 3 %输出:距离矩阵D(i,j),R(i,j) 4 function [d,r]=floyd(w) 5 [m,n]=size(w); 6 if n~=m 7 error('输入的邻接矩阵行数不等于列数!!!'); 8 end 9 %预分配内存空间 10 d=zeros(n,n); 11 r=zeros(n,n); 12 %赋初值 13 for i=1:n 14 for j=1:n 15 d(i,j)=w(i,j); 16 r(i,j)=j; 17 end 18 end 19 k=1; 20 %更新d,r 21 while k<=n 22 for i=1:n 23 for j=1:n 24 if d(i,k)+d(k,j)<d(i,j) 25 d(i,j)=d(i,k)+d(k,j); 26 r(i,j)=r(i,k); 27 end 28 end 29 end 30 k=k+1; 31 end 32 end
求解,

为了直观看出最廉价的线路表,这里编程输出,

1 % DisplayPath.m 打印路径函数 2 function DisplayPath(d,r) 3 % 打印出任意两点之间的最短路径 4 % route : 路由表 5 % start : 起点index 6 % dest : 终点index 7 [m,n]=size(r); 8 if(n~=m) 9 error('输入的路径矩阵有误!!!'); 10 end 11 for i=1:n 12 for j=i:n 13 if i~=j 14 start=i; 15 dest=j; 16 % fprintf('V%d->V%d\t%d$\t\t',i,j,d(i,j));%例题1 17 fprintf('V%d->V%d\t%d\t\t',i,j,d(i,j)); 18 while 1 19 if(r(start, dest) ~= dest) 20 fprintf('V%s -> ', num2str(start)); 21 start = r(start, dest); 22 else 23 fprintf('V%s -> ', num2str(start)); 24 fprintf('V%s\n', num2str(dest)); 25 break; 26 end 27 end 28 end 29 end 30 end
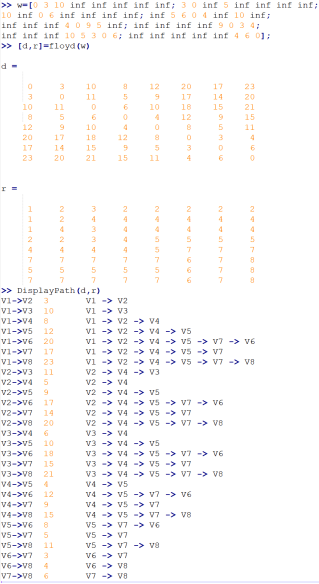
运行示例,

所以,任意两城市之间最廉价的线路表如下:
|
序号 |
始(终) |
终(始) |
线路 |
票价 |
|
1 |
C1 |
C2 |
1→6→2 |
35 |
|
2 |
C1 |
C3 |
1→5→3,1→6→4→3 |
45 |
|
3 |
C1 |
C4 |
1→6→4,1→5→4 |
35 |
|
4 |
C1 |
C5 |
1→5 |
25 |
|
5 |
C1 |
C6 |
1→6 |
10 |
|
6 |
C2 |
C3 |
2→3 |
15 |
|
7 |
C2 |
C4 |
2→4 |
20 |
|
8 |
C2 |
C5 |
2→4→5 |
30 |
|
9 |
C2 |
C6 |
2→6 |
25 |
|
10 |
C3 |
C4 |
3→4 |
10 |
|
11 |
C3 |
C5 |
3→4→5,3→5 |
20 |
|
12 |
C3 |
C6 |
3→4→6 |
35 |
|
13 |
C4 |
C5 |
4→5 |
10 |
|
14 |
C4 |
C6 |
4→6 |
25 |
|
15 |
C5 |
C6 |
5→1→6,5→4→6 |
35 |
(2)解:每一结点到其他结点的最短路,同样使用Floyd算法,MATLAB求解。解得,
(3)解:设狼:1,菜:2,羊:3,人:4。
方法1:
不安全的组合:13,23,123;题目要求转移方案为安全,所以同样不能出现的组合:24,14,4。已知安全的组合:1234,12,34,1,2,3;
人的转移设定可在河中来回(但是只能搭载一样),
由上述分析可知,因为河中只能出现2位和1位(当且仅当对岸的组合是12:3时,人才能独自在河中出现)的组合,第1趟转移的安全组合:12和34;这两个组合中只有34有人也就是说,第一趟转移为:
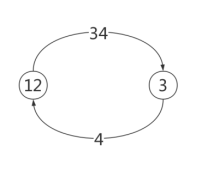
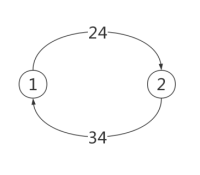
第二趟转移的关键是当人在回航时如果是独自回来的话,那么对岸的情况就是13或23,都是不安全状态,那么只能在回航时带回羊(3)了(因为不带回羊的话,只能带回刚运过去的,这就徒劳无功了)(有两种情况):
 ……
……
只讨论左图的情况(右图以此类推),显然第3趟是把1移过对岸(因为3才运回出发点,并且把1移过去是安全的):
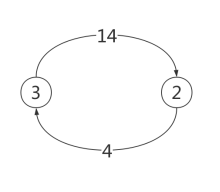
显然,第4趟转移是把3转移过去,从而完美解决题目要求:
综上所述,安全可行(没有多余的无用功)的转移方案有两个,都是4趟转移:
方案1,第一趟:去(羊人),回(人);第二趟:去(狼人),回(羊人);第三趟:去(菜人),回(人);第四趟:去(羊人)。
方案2,第一趟:去(羊人),回(人);第二趟:去(菜人),回(羊人);第三趟:去(狼人),回(人);第四趟:去(羊人)。
方法2:
由组合学知识,
1位组合:1,2,3,4;
2位组合:12,13,14,23,24,34;
3位组合:123,124,134,234;
4位组合:1234。
其中不允许:123,13,23,4,14,24;因此共有10个允许状态,转移关系状态图如下,
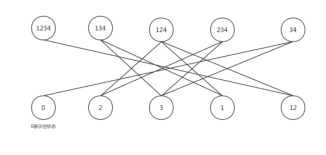
问题归结为求顶点1234到顶点0的最短路,将上图改画为下面形式:
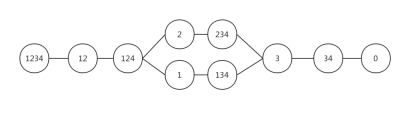
由上图可知,有两种过河方案且等优,如先将羊带到对岸,再将狼带到对岸同时把羊带回原处,将白菜带到对岸,最后把羊带过去。
小结
在编写Floyd程序时,笔者在while循环那里的k值的约束写成了(k<n),运行之后怎么也得不到笔者想要的结果。笔者数次怀疑自己对路径矩阵是不是理解错误了。于是,笔者回看了路径矩阵的数学知识,后来实在忍不住笔者就开始一点一点地修改。在修改2个语句后,突然觉得,是不是循环的条件除了问题,果然是的。后来笔者编写了路径矩阵的输出,发现并不能把同一路线的所有情况输出,可看题1的表,是否有更好的输出算法呢?
附录
【1】最短路问题(1) zlc




