非线性规划（2）

实验目的：

　　学会运用Mathematica、Lingo或Matlab软件求解非线性规划模型。

实验要求：　　

　　实验步骤要有模型建立，模型求解、结果分析。

实验内容：

　　1、一电路由三个电阻R₁,R₂,R₃并联，再与电阻R₄串联而成，记R_k上电流为I_k，电压为V_k，在下列情况下确定R_k，使电路总功率最小（k=1，2，3，4）：

　　（1）I₁=4,I₂=2,I₃=8,2≤V_k≤10;

　　（2）V₁=4,V₂=6,V₃=8,2≤I_k≤10.

　　2、要设计和发射一个带有X射线望远镜和其他科学仪器的气球.对于性能的粗糙的度量方法是以气球所能到达的高度和所携带仪器的重量来表达，很清楚，高度本身是气球体积的一个函数.根据过去的经验作出的结论，是求极大满意性能函数P=f(V,W)=100V-0.3V²+80W-0.2W²,此处V是体积，W是仪器重量.承包项目的预算限额为1040美元，与体积V有关的费用是2V，与设备有关的费用是4W，为了保证在高度方面的性能与科学设备方面的性能之间合理平衡，设计者要满足约束条件80W≥100W.找出由体积和设备重量来表达的最优设计，并用线性化方法求解.

　　3、钢管下料问题.某钢管零售商从钢管厂进货，将钢管按照顾客的要求切割出售.从钢管厂进货得到的原材料钢管的长度都是1850mm，现在一顾客需要15根290mm、28根315mm、21根350mm和30根455mm的钢管.为了简化生产过程，规定所使用的切割模式的种类不能超过4种，使用频率最高的一种切割模式按照一根原料钢管价值的1/10增加费用，使用频率次之的切割模式按照一根原料钢管价值的2/10增加费用，以此类推，且每种切割模式下的切割次数不能太多（一根原料钢管最多生产5根产品），此外，为了减少余料浪费，每种切割模式下的余料浪费不能超过100mm，为了使总费用最小，应该如何下料？

实验步骤：

 　　使用Lingo求解，

model:
sets:
row/1..4/:I,R;
endsets
data:
I=4,6,8,18;
enddata
min=@sum(row(k):I(k)^2*R(k));
@for(row(k):2/I(k)<=R(k));
@for(row(k):R(k)<=10/I(k));
end

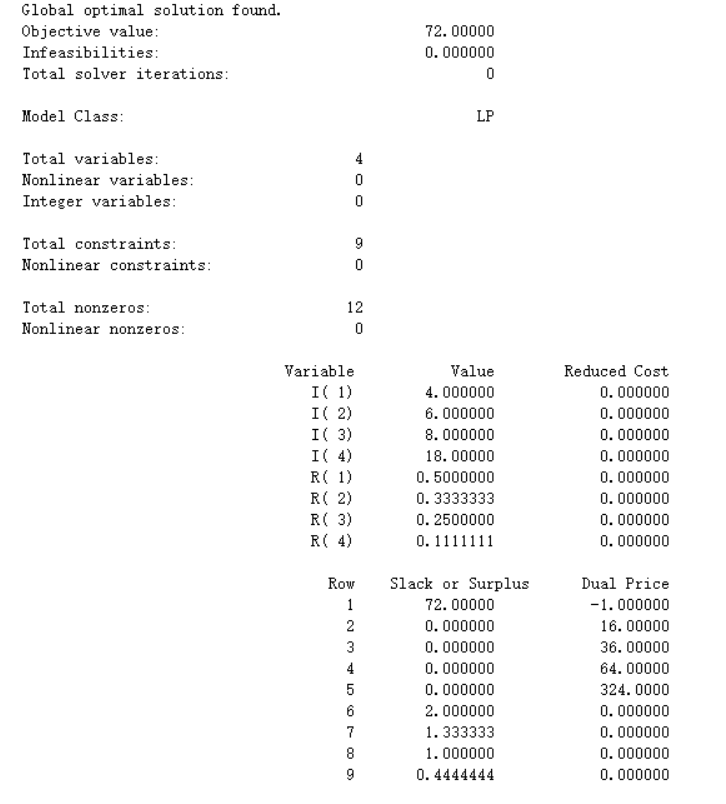
　　解得R₁=0.5,R₂=0.3333333,R₃=0.25,R₄=0.1111111，时使得总功率最小为72。

　　使用Mathematica求解，

(*Nonlinear Programming*)
Minimize[{\!\(
\*SubsuperscriptBox[\(I\), \(1\), \(2\)]*
\*SubscriptBox[\(R\), \(1\)]\)+\!\(
\*SubsuperscriptBox[\(I\), \(2\), \(2\)]*
\*SubscriptBox[\(R\), \(2\)]\)+\!\(
\*SubsuperscriptBox[\(I\), \(3\), \(2\)]*
\*SubscriptBox[\(R\), \(3\)]\)+\!\(
\*SubsuperscriptBox[\(I\), \(4\), \(2\)]*
\*SubscriptBox[\(R\), \(4\)]\),
Subscript[I, 1]==4,Subscript[I, 2]==6,Subscript[I, 3]==8,Subscript[I, 4]==18,
2/Subscript[I, 1]<=Subscript[R, 1] && Subscript[R, 1]<=10/Subscript[I, 1],2/Subscript[I, 2]<=Subscript[R, 2] && Subscript[R, 2]<=10/Subscript[I, 2],
2/Subscript[I, 3]<=Subscript[R, 3] && Subscript[R, 3]<=10/Subscript[I, 3],2/Subscript[I, 4]<=Subscript[R, 4] && Subscript[R, 4]<=10/Subscript[I, 4]
},{Subscript[R, 1],Subscript[R, 2],Subscript[R, 3],Subscript[R, 4]}]

　　

 　　解得R₁=1/2,R₂=1/3,R₃=1/4,R₄=1/9，总功率为72。

 

 

 　　使用Lingo求解，

model:
min=16*x1+36*x2+64*x3+324*x4;
x1<3/2;x1>1/2;
x2<1;x2>1/3;
x3<3/4;x3>1/4;
x4<1/3;x4>1/9;
end
end

　　解得，

　　

　　

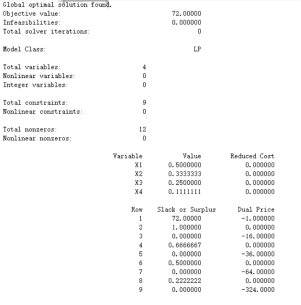
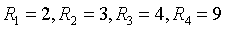
　　总功率为72。

　　使用Mathematica求解,

(*Nonlinear Programming*)
Maximize[{100*v-0.3*v^2+80*w-0.2*w^2,
2v+4w<=1040,
100v-80w<=0,
v>=0,w>=0},{v,w}]

　　

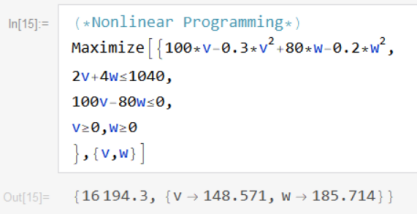
 　　解得v=148.571,w=185.714时，满足设计者的要求，且使得它的满意度最大为16194.3。

　　使用MATLAB求解，

%气球的非线性规划问题
H=[0.6 0;0 0.4];
c=[-100;-80];
A=[2 4;100 -80];
b=[1040;0];
[x,z]=quadprog(H,c,A,b,[],[],[0;0],[]);
x
-z

　　

 　　使用Lingo求解,

model:
max=100*v-0.3*v^2+80*w-0.2*w^2;
2*v+4*w<=1040;
100*v-80*w<=0;
end

　　

 

 　　所以解得v=148.5714,w=185.7143时，满足设计者的要求，且使得它的满意度最大为16194.29。

 　　使用Lingo求解，

model:
sets:
row/1..4/:d,n;
col/1..6/:x;
l/1..5/;
Links(row,col):r;
endsets
data:
d=290,315,350,455;
n=15,28,21,30;
enddata
min=@sum(col(j):x(j)+j*0.1*x(j));
@for(row(i):@sum(col(j):x(j)*r(i,j))>=n(i));
@for(col(j):@sum(row(i):d(i)*r(i,j))>=1750);
@for(col(j):@sum(row(i):d(i)*r(i,j))<=1850);
@for(col(j):@sum(row(i):r(i,j))>=0);
@for(col(j):@sum(row(i):r(i,j))<=5);
@for(col(j):@gin(x(j)));
@for(Links(i,j):@gin(r(i,j)));
@for(l(j):x(j+1)<=x(j));
end

　　运行结果部分截图，

　　

　　解得方案，

　　生产14次模式1——模式1：生产1根290mm钢管，生产2根315mm钢管，生产0根350mm钢管，生产2根455mm钢管；

　　生产4次模式2——模式2：生产0根290mm钢管，生产0根315mm钢管，生产5根350mm钢管，生产0根455mm钢管；

　　生产1次模式3——模式3：生产2根290mm钢管，生产0根315mm钢管，生产1根350mm钢管，生产2根455mm钢管。

　　上述方案中使用了19根原料，其中的290mm钢管多生产了1根。其费用为21.5，把单位1使用a代替，也就是说每根原料的价格为a元。算得最小费用：21.5a元。每次模式1的余料：20mm；每次模式2的余料：100mm；每次模式3的余料：10mm；总余料：690mm。

	290	315	350	455	余料/mm
X1	2	1	0	2	45
X2	1	0	3	1	55
X3	1	2	0	2	20
X4	1	1	2	1	90
X5	0	0	0	4	30
X6	0	1	3	1	30

 

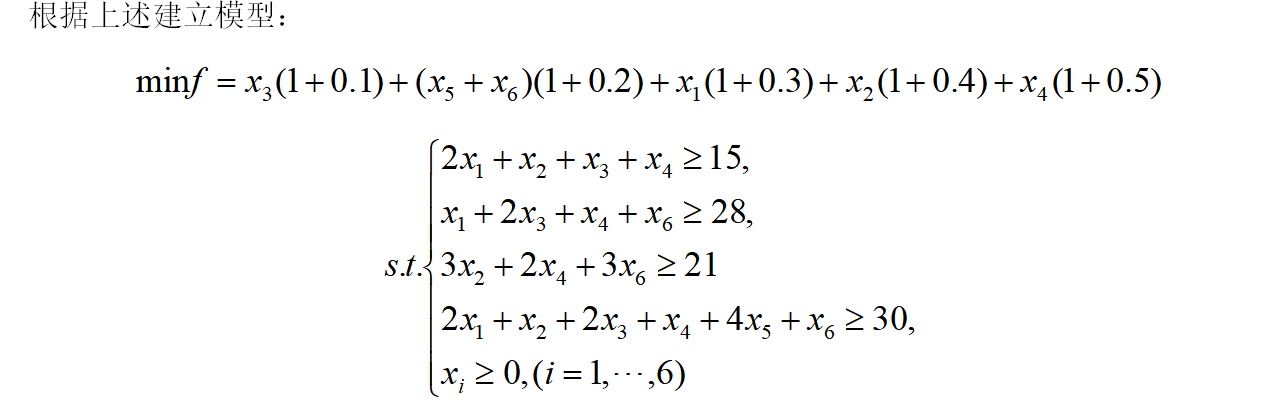
　　使用Lingo求解，

model:
min=0.1*x3+0.2*(x5+x6)+0.3*x1+0.4*x2+0.5*x4+x1+x2+x3+x4+x5+x6;
2*x1+x2+x3+x4>=15;
x1+2*x3+x4+x6>=28;
3*x2+2*x4+3*x6>=21;
2*x1+x2+2*x3+x4+4*x5+x6>=30;
x1>=0;
x2>=0;
x3>=0;
x4>=0;
x5>=0;
x6>=0;
@gin(x1);
@gin(x2);
@gin(x3);
@gin(x4);
@gin(x5);
@gin(x6);
end

　　  

　　使用Mathematica求解，

(*Nonlinear Programming*)
Minimize[{Subscript[x, 3]*1.1+(Subscript[x, 5]+Subscript[x, 6])*1.2+Subscript[x, 1]*1.3+Subscript[x, 2]*1.4+Subscript[x, 4]*1.5,
2*Subscript[x, 1]+Subscript[x, 2]+Subscript[x, 3]+Subscript[x, 4]>=15,
Subscript[x, 1]+2*Subscript[x, 3]+Subscript[x, 4]+Subscript[x, 6]>=28,
3*Subscript[x, 2]+2*Subscript[x, 4]+3*Subscript[x, 6]>=21,
2*Subscript[x, 1]+Subscript[x, 2]+2*Subscript[x, 3]+Subscript[x, 4]+4*Subscript[x, 5]+Subscript[x, 6]>=30,
Subscript[x, 1]>=0,Subscript[x, 2]>=0,Subscript[x, 3]>=0,Subscript[x, 4]>=0,Subscript[x, 5]>=0,Subscript[x, 6]>=0,
Subscript[x, 1]\[Element]Integers,Subscript[x, 2]\[Element]Integers,
Subscript[x, 3]\[Element]Integers,Subscript[x, 4]\[Element]Integers,
Subscript[x, 5]\[Element]Integers,Subscript[x, 6]\[Element]Integers
},{Subscript[x, 1],Subscript[x, 2],Subscript[x, 3],Subscript[x, 4],Subscript[x, 5],Subscript[x, 6]}]

　　 

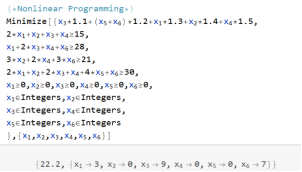
　　解得，当使用方式1到6的次数分别为3，0，9，0，0，7时，使得总费用为22.2。在生产455mm产品时多生产了1根。不过这个模型所使用的原料根数为19与模型1所使用的的原料根数一致。每次模式1的余料：45mm；每次模式3的余料：20mm；每次模式6的余料：30mm；总余料：525mm。

　　模型2在余料方面优于模型1。在多生产的产品里，模型2多生产的是455mm，模型1多生产的是290mm。然而本题只考虑生产成本，因为模型2得到的总费用为22.2a元，大于模型1的21.5a元。所以采用模型1的生产方案。

小结：

　　题目的模型不仅仅只有一个。例如上述题目3所示，不同的模型得到的结果是不一样的。在使用Mathematica编程的过程中，感觉比之MATLAB的编程求解更为之方便，但是必须对所用函数较为熟悉，否则容易得到错解，在模型更为复杂的前提下，更建议使用Lingo求解。

【后话】

　　笔者在解第1题的第（2）问时，可谓是随心所欲（乱写一通）。如，我并没有佐证就杜撰了一个“同样的电阻，串联电路的分路电压之和总大于并联电路的分路电压之和” ，简单地认为同样的条件下，串联电路能达到的最大总电压就是并联电路能达到的最大总电压的上界。同时，不加考证地把每个电阻的最大电压作为目标函数的系数……总而言之，这个解法“粗糙”！

　　当然，这并不是笔者最想说的。笔者更想分享的是第（2）问做的那个电路图的相关操作。详见《浅谈电路图的绘制》。