浅谈分层图最短路
浅谈分层图最短路
1.引言
分层图最短路是一类特殊的最短路问题,主要针对“边权可以有限制地改变”这类问题。
我们先看一个例子:
题目的意思是说,在一个图上,我们可以使用一定次数的“魔法”,使得这些边的边权减半,在此基础上求最短路。
一种最直接的思路是暴力搜索。在dfs中,我们记录目前所在的点、经过的边权总和、还有已经使用魔法的次数。每次对“使用魔法”和“不使用魔法”产生的新状态进行递归。当所用的魔法次数等于使用限制次数\(K\)次的时候,就不能把“使用魔法”作为新状态。
每条边有选与不选两种状态,再加上搜索本身的复杂度,总体时间复杂度过高我不会算,十分容易TLE。
我们不妨从语法的角度进行考虑,分层图最短路中,“分层图”是定语(修饰成分),主语是"最短路"。换句话说,"分层图最短路"还是"最短路"问题,我们依旧要通过已知的最短路算法解决它,只不过需要作出一些魔改变。从哪里改变呢?算法本身?还是......建图?
没错,建图。从建图上解决这类“魔法”问题,就是我们今天要谈论的“分层图最短路”算法。
2.核心内容
由于笔者太蒻,本篇文章只谈论基本的分层图最短路模型。
模型:设有一张图\(G=<V,E>\)(有向无向均可),现有\(K\)个改变边权的机会,可以把任意一条边\(<u,v> =w(<u,v>\in E)\)的边权改变一次(若对于无向图,是改变无向边\((u,v)\)),变为\(w'\)。在此基础上求点\(S,T(S,T\in V)\)之间的最短路。
算法:
1.将原图复制\(K\)份(和原图加起来总共有\(K+1\)个图),原图记作\(G_0\),其它图分别记作\(G_1,G_2,...,G_K\)。\(G_1\)到\(G_K\)每一张图,都按照原图\(G_0\)的方式连边,边权均相同。
这样做的目的是什么呢?我们可以考虑,每一层图\(G_i(0\le i \le K)\)都对应"改变边权的机会"使用了\(i\)次的状态。比如说你改变了 \(2\) 次边权,那么你现在就在\(G_2\)上,特殊地,一次机会都没用,就在原图\(G_0\)上。值得一提的是,只要\(w'\)不为负数,最短路就不会经过一条边两次,所以这里还要补充一点:每条边在使用机会时,边权只会在你经过的这一次临时改变,经过之后立刻恢复原边权。(其实大多数的题都有这种要求)所以我们可以认为,使用了机会以后,图本身是不变的。
接下来我们考虑,每层之间如何连边。
2.对于边\(<u,v>or(u,v)\in G_0\),如果一次机会会使\(<u,v>\)的边权\(w\)变为\(w'\),则分别找到\(u\)在\(G_0 \sim G_{K-1}\)里的对应点\(u_0\sim u_{K-1}\)(其实\(u_0\)就是\(u\)本身),找到\(v\)在\(G_1\sim G_K\)里的对应点\(v_1\sim v_K\),对于每个\(i\in[0,K-1]\),从\(u_i\)向\(v_{i+1}\)连一条边,这样总共连\(K-1\)条,每条边的边权都为\(w'\)。
举个栗子,设原图有三条有向边\(<1,2>,<2,3>,<1,3>\),边权分别为\(8,6,2\),有\(2\)次机会,每次"机会"是将边权减半,画出图来大概是这个亚子:
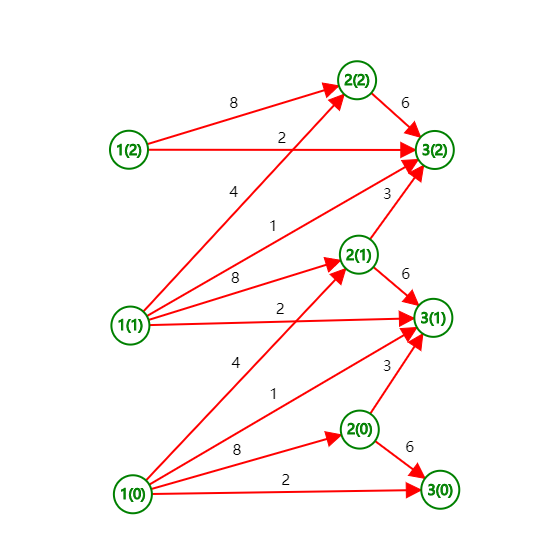
太乱了?我们可以只看其中\(<1,2>\)的一部分:
.png)
就像这样,每条边的终点"上移一层"形成新的边,边权即为使用"机会"后的边权,形成类似楼梯的结构奇妙的比喻。这样,我们就建好了一个\(K+1\)层的连通图。
这样做的目的是形成状态之间的转移。我们可以发现,我们可以通过使用一次机会,从"使用了\(i\)次机会的"状态图转移到"使用了\(i+1\)次机会的状态图"。同时向上一层连边的边权减半,也正好意味着在这条边上使用了一次"机会",最后到达的还是原边对应的终点(只不过是层数不同,本质是一样的)。由于每层没有向下一层返回的路径,所以我们可以保证最多使用\(K\)次机会。
3.处理终点,这里我们需要分情况讨论:
(1)设原图\(G_0\)所有边(不使用机会)的最小边权为\(w_{min}\),设对于任意一条边使用机会后的边权\(w'\),都有\(w'\le w_{min}\),则我们可以贪心地认为,最短路一定使用了所有\(K\)次机会,于是设终点\(T\)在最高一层\(G_K\)上对应的点为\(T_K\),起点为\(S\)(一定在第\(0\)层),则答案就是\(S\)到\(T_K\)的最短路。
(2)否则,最短路不一定使用了所有\(K\)次机会(毕竟有的边不使用机会,也比有的边使用机会更优),这时候我们可以从终点\(T\)在所有层图中对应的所有点\(T_0\sim T_K\)向一个“超级终点"\(T'\)连边,边权为\(0\),求起点\(S\)到超级终点\(T'\)的最短路即可。或者还是求\(S\)到\(T_K\)的最短路,然后遍历所有\(T_0\sim T_K\)在求最短路时产生的\(dist\)值,取最小值即可。
这样相当于遍历使用任意次机会的所有情况。
这就是分层图最短路最基本模型的思路。这里附上本文开头所给题目的代码:这里我们常常规定点\(p\)在第\(1,2,3...\)层对应的点分别为\(p+n,p+2n,p+3n...\)。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define FLOOR(x,floor) ((x)+(n)*(floor))//求点x在第floor层对应的点
using namespace std;
const int MAXN = 10000004, MAXM = 50000004;//这里开大一点,至少要N*K。
int ver[MAXN], edge[MAXN], nxt[MAXN], head[MAXN], tot;
void add_edge(int u, int v, int w)//正常的链式前向星加边操作
{
ver[++tot] = v;
edge[tot] = w;
nxt[tot] = head[u];
head[u] = tot;
}
namespace Dijkstra {
bool vis[MAXN];
int dist[MAXN];
priority_queue<pair<int, int>> q;
int dij(int start, int end) {//正常的Dijkstra,注意若有负权边则需使用Bellman-ford或spfa
memset(vis, 0, sizeof(vis));
memset(dist, 0x3f, sizeof(dist));
dist[start]=0;
q.push(make_pair(0, 1));
while (!q.empty()) {
int x=q.top().second;
q.pop();
for (int i=head[x];i;i=nxt[i]) {
int y=ver[i], w=edge[i];
if (dist[y]>dist[x]+w) {
dist[y]=dist[x]+w;
q.push(make_pair(-dist[y], y));
}
}
}
return dist[end];
}
}
int n, m, k;
int main() {
scanf("%d%d%d", &n, &m, &k);
for (int i=1, x, y, z;i<=m;i++) {
scanf("%d%d%d", &x, &y, &z);
for (int f=0;f<=k;f++) {
add_edge(FLOOR(x, f), FLOOR(y, f), z);//每层内部连边(由于是无向边,拆成两条有向边处理)
add_edge(FLOOR(y, f), FLOOR(x, f), z);
}
for (int f=0;f<=k-1;f++) {
add_edge(FLOOR(x, f), FLOOR(y, f+1), z/2);//每层之间连边
add_edge(FLOOR(y, f), FLOOR(x, f+1), z/2);
}
}
for (int f=0;f<=k;f++) {
add_edge(FLOOR(n, f), 0, 0);//设0号点为“超级终点”
}
printf("%d\n", Dijkstra::dij(1, 0));
return 0;
}
3.三倍经验
稍微修改一下就能爆切。



