队列与广度优先搜索概述+一本通1362
在C++中有很多数据结构,包括栈(stack)、队列(queue)、容器(vector)、数对(pair)等。这篇博客的重点是队列。
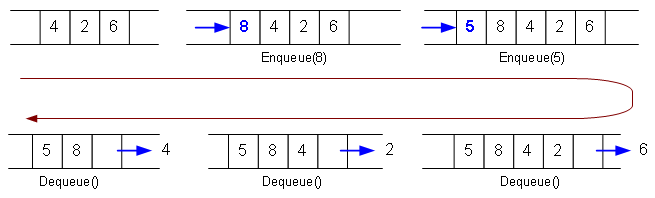
1.队列的定义:一种线性数据结构,可以插入和弹出数据。每个队列除了有数据,还有两个指针,“头指针”指向队列的第一个元素(以下简称队首),“尾指针”指向队列的最后一个元素(以下简称队尾)。插入数据时在队列的队尾后插入,并使尾指针后移一位。弹出时是弹出队首的元素,并使头指针后移一位。也就是说,先插入的元素会先被弹出,这一特性叫做“先进先出”(FIFO,“First in first out”)。
以下是一个队列的例子,其中Enqueue函数是插入操作,Dequeue函数是弹出操作。
(来自百度)
2.队列的基本操作:
(1)头文件:<queue>
(2)声明一个队列:queue<typename T> q; (typename是指队列中存放的数据类型,最常见的如int、char)
(3)插入操作:void push(T a);(这里是指a的类型由上述typename决定,下同)
(4)弹出操作:void pop();
(5)获得队首元素:T front();
(6)获得队尾元素:T back();
(7)获得队列里的元素数量:size_type size();
(8)检验队列是否为空:bool empty();
3.广度优先搜索(bfs)是指从当前节点访问所有与它相邻的节点(称为第一层),全部访问完以后,再访问与第一层相连的所有节点(第二层)......以此类推,直到所有节点都搜索完为止。
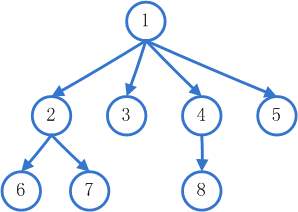
上面的树,广度优先搜索会得到以下的搜索次序:1 2 3 4 5 6 7 8 。而深度优先搜索则是:1 2 6 7 3 4 8 5。
队列是一端插入,另一端弹出的线性数据结构,这给广度优先搜索的实现带来了极大便利。先把根节点插入队列,再插入与它相连的节点,依次访问,访问节点的同时把与它相连的节点插入队列,访问后弹出该节点。若队列为空,则证明搜索结束。
4.例题(ybt1362:家庭问题(family))
【题目描述】有n个人,编号为1,2,……n,另外还知道存在K个关系。一个关系的表达为二元组(α,β)形式,表示α,β为同一家庭的成员。当n,k和k个关系给出之后,求出其中共有多少个家庭、最大的家庭中有多少人?例如:n=6,k=3,三个关系为(1,2),(1,3),(4,5)此时,6个人组成三个家庭,即:{1,2,3}为一个家庭,{4,5}为一个家庭,{6}单独为一个家庭,第一个家庭的人数为最多。
【输入】第一行为n,k二个整数(1≤n≤100)(用空格分隔);接下来的k行,每行二个整数(用空格分隔)表示关系。
【输出】二个整数(分别表示家庭个数和最大家庭人数)。
【输入样例】
6 3
1 2
1 3
4 5
【输出样例】
3 3
代码如下:(以下代码用到了pair,它表示一个数组,包含于iostream里,第一个数用first表示,第二个用second表示)
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<queue> 5 using namespace std; 6 int n,k; 7 pair<int,int> rela[1000];//记录一对关系 8 int inWhichFamily[105];//记录每个人在编号为几的家庭中,0表示这个人独自成为一个家庭 9 queue<int> family[105];//模拟家庭 10 11 int main() 12 { 13 cin>>n>>k; 14 int p=1;//目前的家庭编号 15 for(int i=1;i<=k;i++) 16 { 17 cin>>rela[i].first>>rela[i].second; 18 if((!inWhichFamily[rela[i].first])&&(!inWhichFamily[rela[i].second])&&rela[i].first!=rela[i].second)//这对关系不属于任何一个家庭,是一个新家庭。(注意排除关系的两个人相同的情况) 19 { 20 family[p].push(rela[i].first);//新家庭的两个人 21 family[p].push(rela[i].second); 22 inWhichFamily[rela[i].first]=p;//这两个人属于第p个家庭 23 inWhichFamily[rela[i].second]=p; 24 p++;//家庭数量增加 25 } 26 else if((!inWhichFamily[rela[i].first])&&(inWhichFamily[rela[i].second]))//有个人已经有所属家庭 27 { 28 family[inWhichFamily[rela[i].second]/*那个人所属家庭的编号*/].push(rela[i].first);//将另一个人加入这个家庭中 29 inWhichFamily[rela[i].first]=inWhichFamily[rela[i].second];//这个人获得了家庭编号 30 } 31 else if((inWhichFamily[rela[i].first])&&(!inWhichFamily[rela[i].second]))//与上面的同理 32 { 33 family[inWhichFamily[rela[i].first]].push(rela[i].second); 34 inWhichFamily[rela[i].second]=inWhichFamily[rela[i].first]; 35 } 36 } 37 int _max=1; 38 for(int i=1;i<=n;i++) 39 { 40 // cout<<family[i].size(); 41 if(!inWhichFamily[i]) p++;//再考虑独自成家的人 42 if(family[i].size() > (unsigned)_max)//得到最大的家庭大小 43 { 44 _max=family[i].size(); 45 } 46 } 47 cout<<p-1<<" "<<_max<<endl;//前面应该是多加了一个1 48 }
好像和广度优先搜索没什么关系......算了不管了,开溜