Trie-前缀查询

Tire专门为处理字符串设计的。

• 平衡二叉树，查询复杂度是O(logn)
• 但是100万个条目，2^20，logn大约20.
• 但是Tire的复杂度，和字段中一共有多少条目无关！世间复杂度为O（w），w为查询单词的长度
• 大多数的单词长度小于10

图示

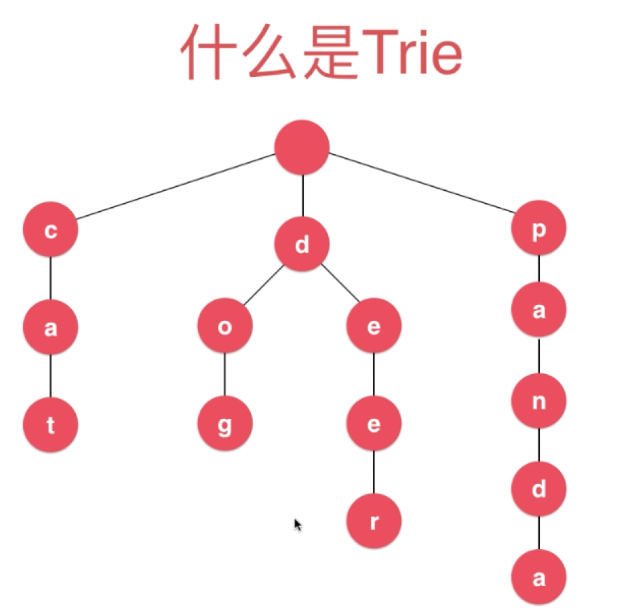
整个字符串以字母为单位拆开

cat、dog、deer、panda

 

可以看出

每个节点有26个指向下一节点的指针。(不考虑大小写)（不同的内容，子树数量不确定。）

从根节点出发，有26个子树。

class Node{

　　char c;

　　Map<char, Node> next;

}

 

继而，在找cat的时候，寻找c之前，就已经知道目标地址存储c了。

所以这样表达就可以。

class Node{

　　Map<char, Node> next;

}

 

叶子结点 单词的结尾靠叶子结点不能表示出。

panda中 pan是平底锅的结尾 ， 所以要加一个布尔值，判断每个节点是否是一个单词。

class Node{

　　boolean isWord；

　　Map<char, Node> next;

}

代码实现

import java.util.TreeMap;

/**
 * trie数定义
 */
public class Trie {
    /*
     * 子节点
     */
    private class Node{
        public boolean isWord;
        //默认节点是字符型，不采用泛型来设计。字符串是由一个字符组成的。主要用于字符串。主要用于英语语境
        public TreeMap<Character, Node> next;

        public Node(boolean isWord){
            this.isWord = isWord;
            next = new TreeMap<>();
        }
        public Node(){
            this(false);
        }
    }

    private Node root;
    private int size;

    public Trie(){
        root = new Node();
        size = 0;
    }

    public int getSize(){
        return size;
    }

    /**
     * 新增单词的方法
     * @param word
     */
    public void add(String word){
        Node cur = root;
        for (int i = 0; i < word.length(); i++) {
            char c = word.charAt(i);
            if(cur.next.get(c) == null){
                cur.next.put(c, new Node());
            }
            cur = cur.next.get(c);
        }
        if(!cur.isWord){
            cur.isWord = true;
            size++;
        }
    }

　　
}

 

    /**
     * 判断是否存在word
     * @param word
     * @return
     */
    public boolean containsWord(String word){
        Node cur = root;
        for (int i = 0; i < word.length(); i++) {
            char c = word.charAt(i);
            if(cur.next.get(c) == null){
                return false;
            }
            cur = cur.next.get(c);
        }
        return cur.isWord;
    }

 

前缀搜索

    /**
     * 判断是否存在 前缀判断
     * @param prefix
     * @return
     */
    public boolean containsPrefix(String prefix){
        Node cur = root;
        for (int i = 0; i < prefix.length(); i++) {
            char c = prefix.charAt(i);
            if(cur.next.get(c) == null){
                return false;
            }
            cur = cur.next.get(c);
        }
        return true;
    }

    

 

相关算法题

208题 https://leetcode.cn/problems/implement-trie-prefix-tree/description/

211题 https://leetcode.cn/problems/design-add-and-search-words-data-structure/description/

 

 

拓展

空间消耗大 》 

压缩字典树

 

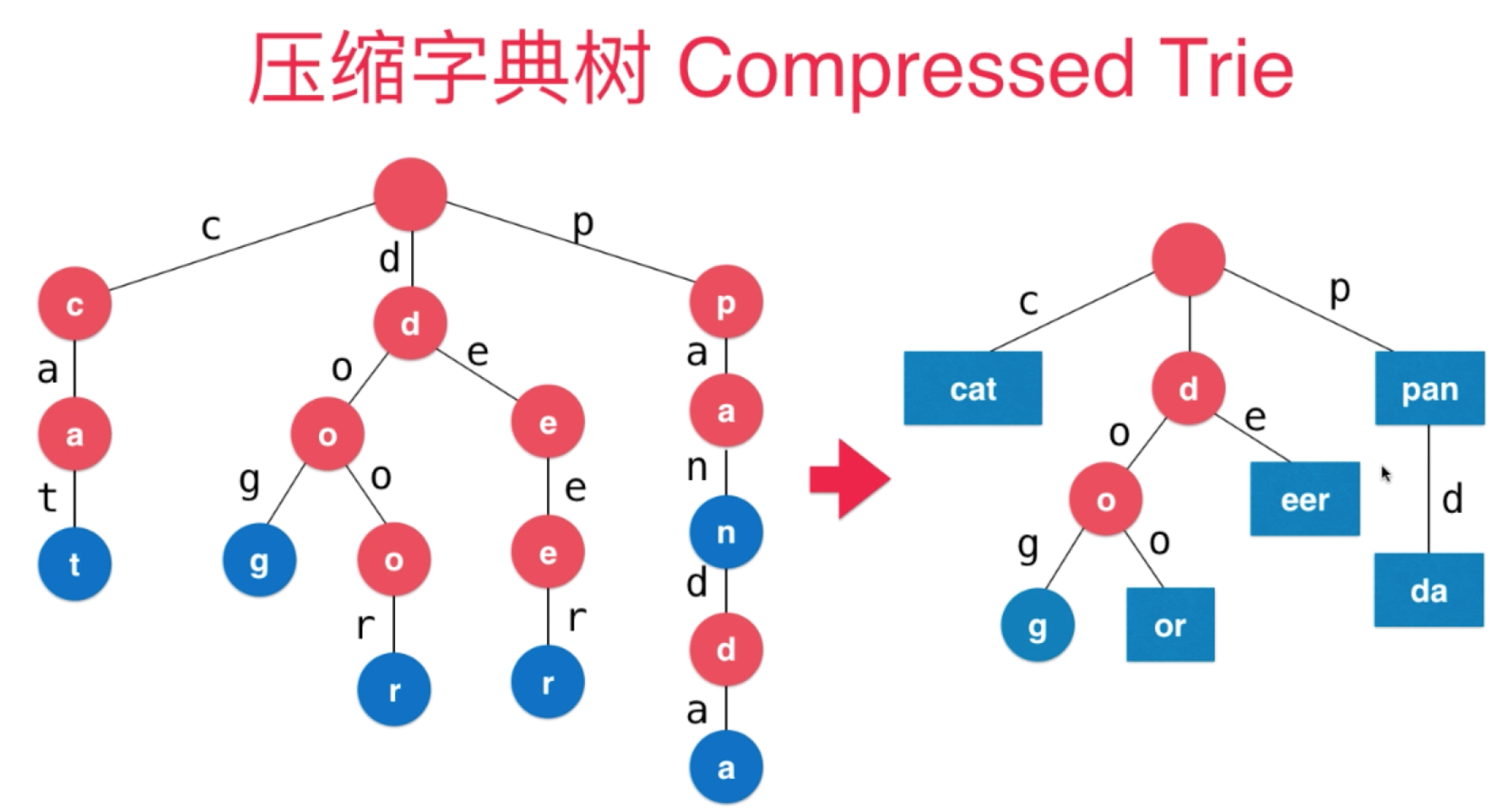
三分搜索树 牺牲了一定的时间 但是总的时间复杂度还是和字符串长度正相关

 

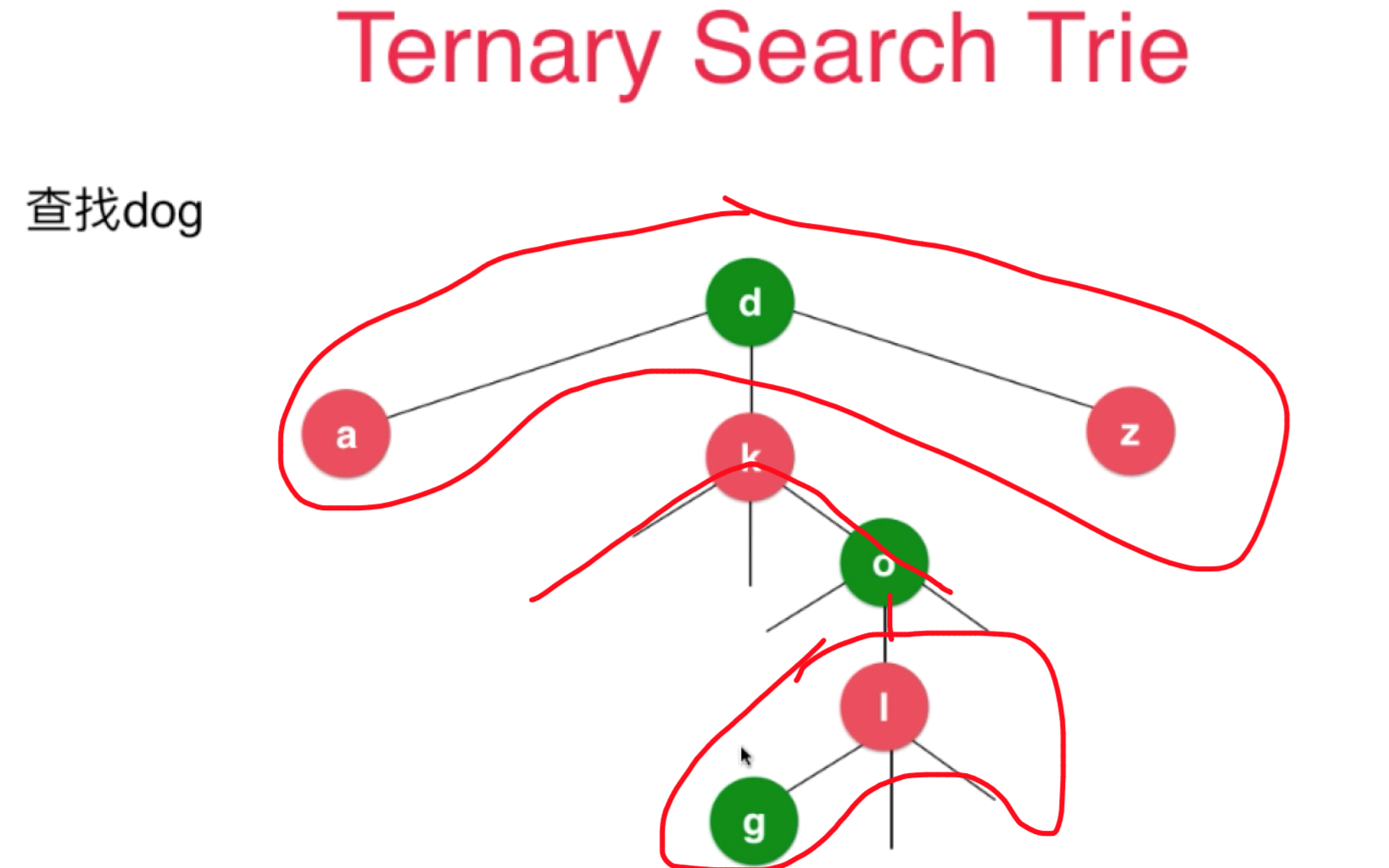
后缀树