nlp RNNLM
2022-04-05 14:59 jym蒟蒻 阅读(398) 评论(0) 收藏 举报RNNLM
基于RNN的语言模型称为RNNLM(Language Model)。
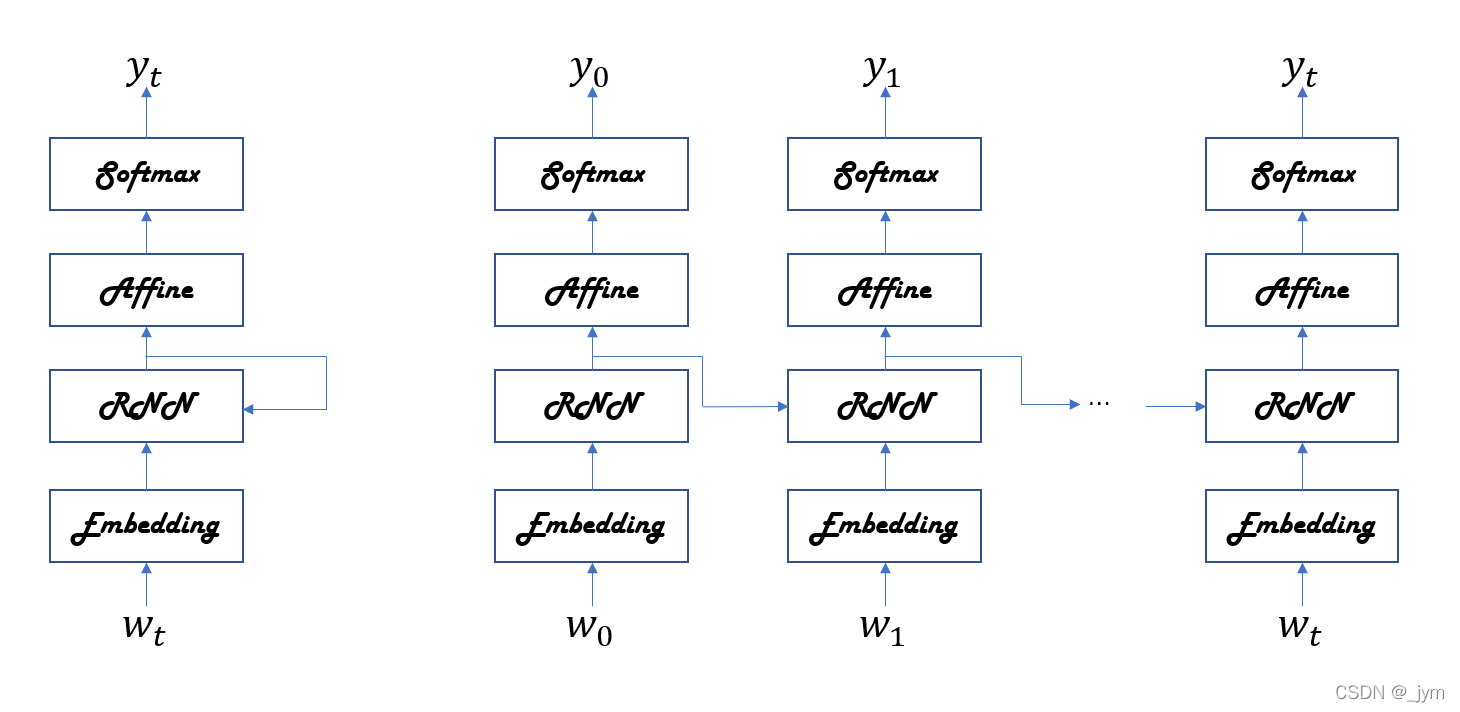
Embedding 层:将单词ID转化为单词的分布式表示(单词向量)。
RNN层:向下一层(上方)输出隐藏状态,同时也向下一时刻的RNN层(右边)输出隐藏状态。
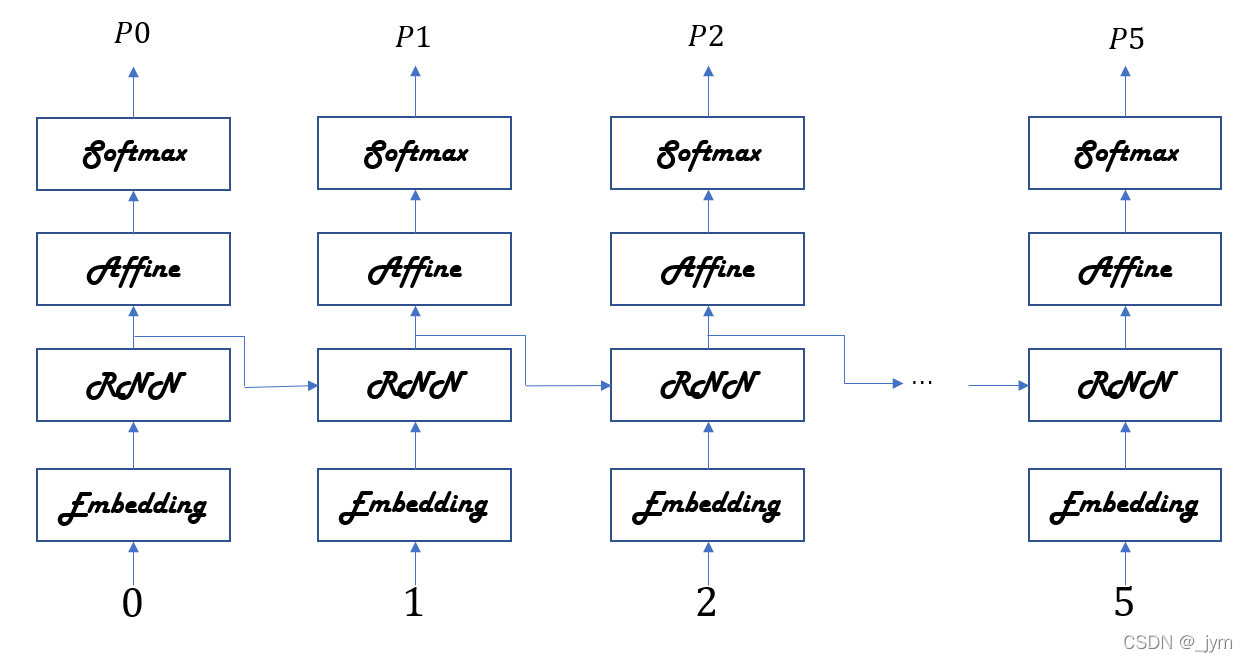
对于“you say goodbye and i say hello.”如果模型学习顺利。
输入的数据是单词ID列表,输入单词ID为0的you,Softmax层输出的概率分布P0中,say的概率最高。这说明预测出了you后面出现的单词为say。
输入单词ID为1的say,Softmax层输出的概率分布P1中,goodbye和hello的概率最高。RNN层记忆了you say这一上下文。RNN将you say这一过去的信息保存成隐藏状态向量。
RNNLM可以记忆目前为止输入的单词,并以此为基础预测接下来会出现的单词。
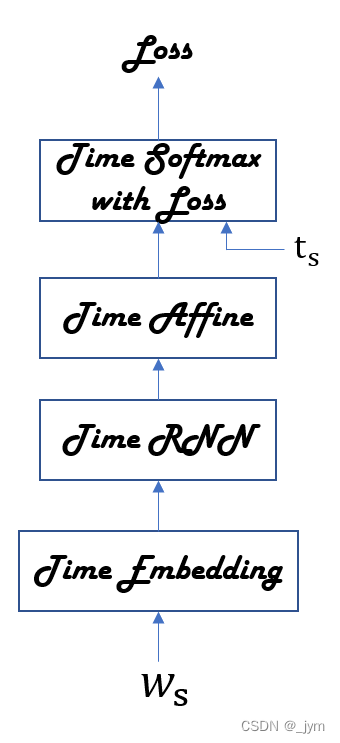
如果整体处理时序数据,神经网络就如下图所示。整体处理含有T个时序数据的层称为Time xx层。
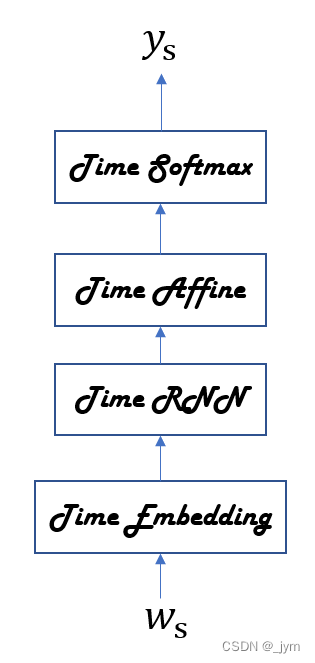
Time Affine 层:使用T个Affine层分别处理各个时刻的数据。代码使用矩阵运算实现整体处理。
class TimeAffine:
def __init__(self, W, b):#接收权重参数和偏置参数
self.params = [W, b]#参数设置为列表类型的成员变量params
self.grads = [np.zeros_like(W), np.zeros_like(b)]
self.x = None
def forward(self, x):#x包含T个时序数据
N, T, D = x.shape#批大小是 N,输入向量的维数是 D,x形状为(N,T,D)
W, b = self.params
rx = x.reshape(N*T, -1)
out = np.dot(rx, W) + b#使用矩阵运算实现整体处理
self.x = x
return out.reshape(N, T, -1)
def backward(self, dout):
x = self.x
N, T, D = x.shape
W, b = self.params
dout = dout.reshape(N*T, -1)
rx = x.reshape(N*T, -1)
db = np.sum(dout, axis=0)
dW = np.dot(rx.T, dout)
dx = np.dot(dout, W.T)
dx = dx.reshape(*x.shape)
self.grads[0][...] = dW
self.grads[1][...] = db
return dx
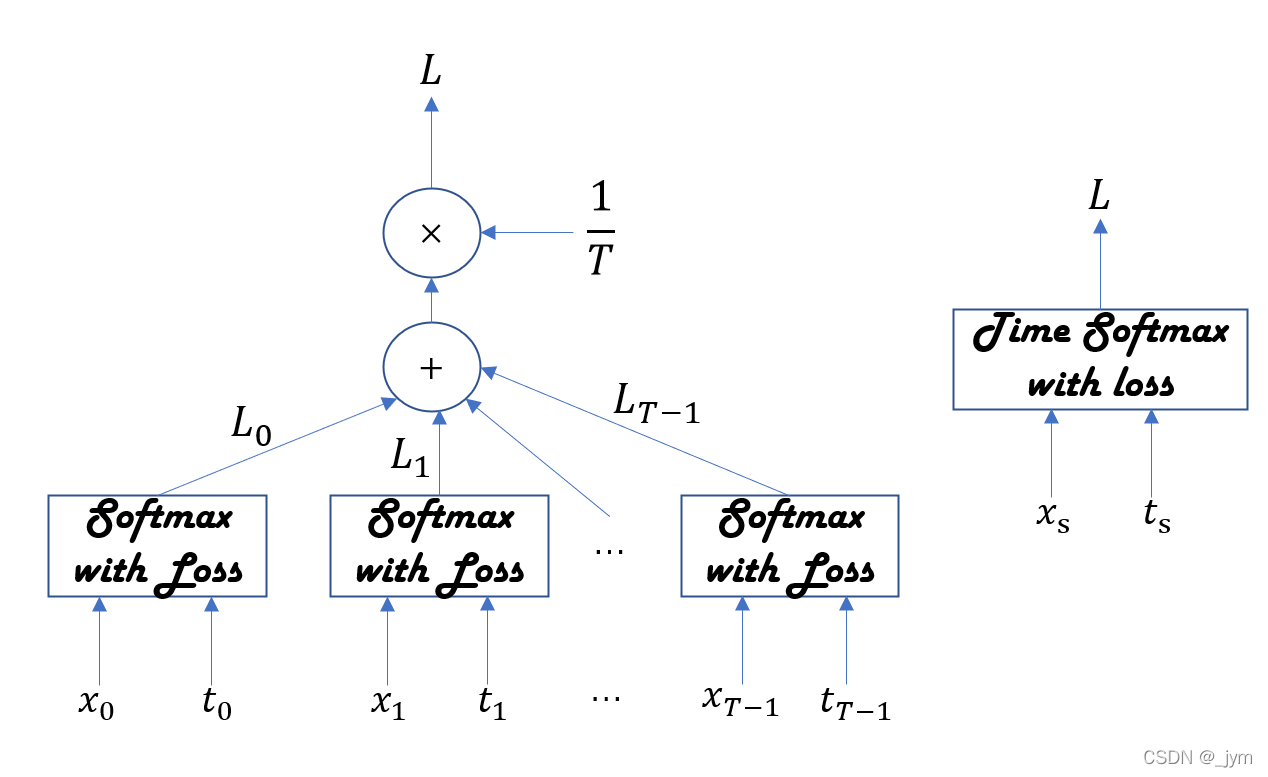
Time Softmax with Loss 层:
x表示从下方的层传来的得分(正规化为概率之前的值);t表示正确解标签;T个Softmax with Loss层各自算出损失,相加并求平均,得到的值作为最终的损失。
class TimeSoftmaxWithLoss:
def __init__(self):
self.params, self.grads = [], []
self.cache = None
self.ignore_label = -1
def forward(self, xs, ts):
N, T, V = xs.shape
if ts.ndim == 3: # 在监督标签为one-hot向量的情况下
ts = ts.argmax(axis=2)
mask = (ts != self.ignore_label)
# 按批次大小和时序大小进行整理(reshape)
xs = xs.reshape(N * T, V)
ts = ts.reshape(N * T)
mask = mask.reshape(N * T)
ys = softmax(xs)
ls = np.log(ys[np.arange(N * T), ts])
ls *= mask # 与ignore_label相应的数据将损失设为0
loss = -np.sum(ls)
loss /= mask.sum()
self.cache = (ts, ys, mask, (N, T, V))
return loss
def backward(self, dout=1):
ts, ys, mask, (N, T, V) = self.cache
dx = ys
dx[np.arange(N * T), ts] -= 1
dx *= dout
dx /= mask.sum()
dx *= mask[:, np.newaxis] # 与ignore_label相应的数据将梯度设为0
dx = dx.reshape((N, T, V))
return dx
将RNNLM使用的网络实现为SimpleRnnlm类,结构如下。
class SimpleRnnlm:
def __init__(self, vocab_size, wordvec_size, hidden_size):
V, D, H = vocab_size, wordvec_size, hidden_size
rn = np.random.randn
# 初始化权重,对各个层使用的参数(权重和偏置)进行初始化
embed_W = (rn(V, D) / 100).astype('f')
rnn_Wx = (rn(D, H) / np.sqrt(D)).astype('f')
rnn_Wh = (rn(H, H) / np.sqrt(H)).astype('f')
rnn_b = np.zeros(H).astype('f')
affine_W = (rn(H, V) / np.sqrt(H)).astype('f')
affine_b = np.zeros(V).astype('f')
'''
使用 Truncated BPTT 进行学习,将 Time RNN 层的 stateful设置为 True
Time RNN 层就可以继承上一时刻的隐藏状态
RNN 层和 Affine 层使用了Xavier 初始值
'''
# 生成层
Time RNN 层就可以继承上一时刻的隐藏状态
self.layers = [
TimeEmbedding(embed_W),
TimeRNN(rnn_Wx, rnn_Wh, rnn_b, stateful=True),
TimeAffine(affine_W, affine_b)
]
self.loss_layer = TimeSoftmaxWithLoss()
self.rnn_layer = self.layers[1]
# 将所有的权重和梯度整理到列表中
self.params, self.grads = [], []
for layer in self.layers:
self.params += layer.params
self.grads += layer.grads
def forward(self, xs, ts):
for layer in self.layers:
xs = layer.forward(xs)
loss = self.loss_layer.forward(xs, ts)
return loss
def backward(self, dout=1):
dout = self.loss_layer.backward(dout)
for layer in reversed(self.layers):
dout = layer.backward(dout)
return dout
def reset_state(self):
self.rnn_layer.reset_state()
常使用困惑度(perplexity)评价语言模型。
困惑度是概率的倒数(数据量为1时),因为预测出的正确单词的概率越大越好,所以困惑度越小越好。
困惑度可以解释为分叉度,表示下一个可以选择的选项的数量(下一个可能出现单词的候选个数)。
输入数据为多个的情况,困惑度计算:
L是神经网络的损失,数据量为N个,tn是one-hot向量形式正确解标签,tnk表示第n个数据的第k个值,ynk是概率分布(神经网络Softmax的输出)。
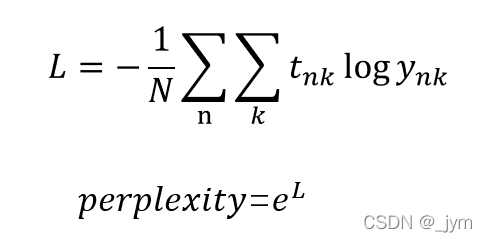
RNNLM的学习和评价的代码如下。
# 设定超参数
batch_size = 10
wordvec_size = 100
hidden_size = 100
time_size = 5 # Truncated BPTT的时间跨度大小
lr = 0.1
max_epoch = 100
# 读入训练数据(缩小了数据集)
corpus, word_to_id, id_to_word = ptb.load_data('train')
corpus_size = 1000
corpus = corpus[:corpus_size]
vocab_size = int(max(corpus) + 1)
xs = corpus[:-1] # 输入
ts = corpus[1:] # 输出(监督标签)
data_size = len(xs)
print('corpus size: %d, vocabulary size: %d' % (corpus_size, vocab_size))
# 学习用的参数
max_iters = data_size // (batch_size * time_size)
time_idx = 0
total_loss = 0
loss_count = 0
ppl_list = []
# 生成模型
model = SimpleRnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)
'''
使用 Truncated BPTT 进行学习,因此数据需要按顺序输入.
mini-batch 的各批次要平移读入数据的开始位置。
'''
# 计算读入mini-batch的各笔样本数据的开始位置
jump = (corpus_size - 1) // batch_size
offsets = [i * jump for i in range(batch_size)]#offsets 的各个元素中存放了读入数据的开始位置
for epoch in range(max_epoch):
for iter in range(max_iters):
# 获取mini-batch,按顺序读入数据
batch_x = np.empty((batch_size, time_size), dtype='i')
batch_t = np.empty((batch_size, time_size), dtype='i')
for t in range(time_size):#
for i, offset in enumerate(offsets):#各批次增加偏移量
batch_x[i, t] = xs[(offset + time_idx) % data_size]#将time_idx 处的数据从语料库中取出,将当前位置除以语料库大小后的余数作为索引使用
batch_t[i, t] = ts[(offset + time_idx) % data_size]#取余数为的是:读入语料库的位置超过语料库大小时,回到语料库的开头
time_idx += 1
# 计算梯度,更新参数
loss = model.forward(batch_x, batch_t)
model.backward()
optimizer.update(model.params, model.grads)
total_loss += loss
loss_count += 1
# 各个epoch的困惑度评价
ppl = np.exp(total_loss / loss_count)#计算每个 epoch 的平均损失,然后计算困惑度
print('| epoch %d | perplexity %.2f'
% (epoch+1, ppl))
ppl_list.append(float(ppl))
total_loss, loss_count = 0, 0
# 绘制图形
x = np.arange(len(ppl_list))
plt.plot(x, ppl_list, label='train')
plt.xlabel('epochs')
plt.ylabel(