nlp 二分类 改进CBOW

二分类负采样方法

多分类问题处理为二分类问题，需要能够正确地对正例和负例进行分类。

如果以所有的负例为对象，词汇量将增加许多，无法处理。作为一种近似方法，将只使用少数负例。

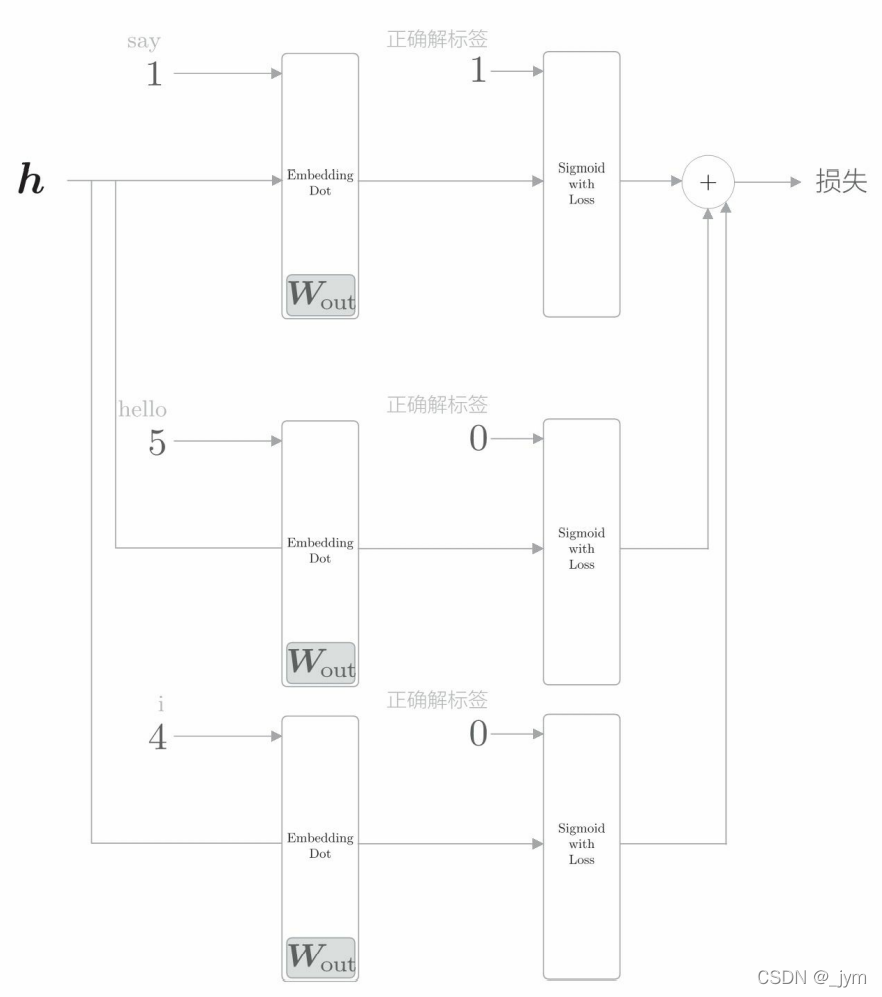
负采样方法：求正例作为目标词时的损失，同时采样(选出)若干个负例，对这些负例求损失。然后，将正例和采样出来的负例的损失加起来，作为最终的损失。例子如下图所示。

负采样的采样方法：

抽取负例：让语料库中常出现的单词易被抽到，不常出现的单词难被抽到。

基于频率的采样方法：计算语料库中各个单词的出现次数，并将其表示为概率分布，然后使用这个概率分布对单词进行采样。

通过给np.random.choice函数参数p，指定表示概率分布的列表，将进行基于概率分布的采样。

import numpy as np
words = ['you', 'say', 'goodbye', 'I', 'hello', '.']
a = np.random.choice(words)
b = np.random.choice(words, size=5)
c = np.random.choice(words, size=5, replace=False)
p = [0.5, 0.1, 0.05, 0.2, 0.05, 0.1]
d = np.random.choice(words, p=p)
print(a)
print(b)
print(c)
print(d)

输出：

hello
['.' 'hello' 'hello' 'goodbye' 'goodbye']
['hello' '.' 'goodbye' 'you' 'I']
you

word2vec中的负采样：对原来的概率分布取0.75次方。分子表示第i个单词的概率。分母是变换后的概率分布的总和。(使变换后的概率总和仍为1)，通过取0.75次方，低频单词的概率将稍微变高。作为一种补救措施，使得变换后低频单词比变换前抽到的几率增加。

以1个连续单词(unigram)为对象创建概率分布，进行负例抽取的函数如下。corpus是是单词ID列表；power是概率分布取的次方值；sample_size是负例的采样个数。

如果是bigram，则以(you,say)、(you,goodbye)这样的2个单词的组合为对象创建概率分布。

class UnigramSampler:
    def __init__(self, corpus, power, sample_size):
        self.sample_size = sample_size
        self.vocab_size = None
        self.word_p = None

        counts = collections.Counter()
        for word_id in corpus:
            counts[word_id] += 1

        vocab_size = len(counts)
        self.vocab_size = vocab_size

        self.word_p = np.zeros(vocab_size)
        for i in range(vocab_size):
            self.word_p[i] = counts[i]

        self.word_p = np.power(self.word_p, power)
        self.word_p /= np.sum(self.word_p)

    def get_negative_sample(self, target):
        batch_size = target.shape[0]

        if not GPU:
            negative_sample = np.zeros((batch_size, self.sample_size), dtype=np.int32)

            for i in range(batch_size):
                p = self.word_p.copy()
                target_idx = target[i]
                p[target_idx] = 0
                p /= p.sum()
                negative_sample[i, :] = np.random.choice(self.vocab_size, size=self.sample_size, replace=False, p=p)
        else:
            # 在用GPU(cupy）计算时，优先速度
            # 有时目标词存在于负例中
            negative_sample = np.random.choice(self.vocab_size, size=(batch_size, self.sample_size),
                                               replace=True, p=self.word_p)

        return negative_sample

使用这个类：[1, 3, 0]这3个数据的mini-batch作为正例，对各个数据采样2个负例。

import numpy as np
from negative_sampling_layer import UnigramSampler
corpus = np.array([0, 1, 2, 3, 4, 1, 2, 3])
power = 0.75
sample_size = 2
sampler = UnigramSampler(corpus, power, sample_size)
target = np.array([1, 3, 0])
negative_sample = sampler.get_negative_sample(target)
print(negative_sample)

输出：可以看到每个数据的负例。

[[2 4]
 [2 0]
 [2 1]]

实现负采样层：

参数：输出侧权重W，单词ID列表corpus，概率分布的次方值power，负例的采样数sample_size， sampler保存UnigramSampler生成的采样负例。

loss_layers 和 embed_dot_layers 中以列表格式保存了必要的层，生成sample_size + 1 个层，意味着生成一个正例用的层和 sample_size 个负例用的层。loss_layers[0] 和 embed_dot_layers[0] 是处理正例的层。

正向传播：通过 Embedding Dot 层的 forward 输出得分，再将得分和标签一起输入 Sigmoid with Loss 层来计算损失和。

反向传播：以与正向传播相反的顺序调用各层的 backward() 函数，将多份梯度累加起来。

class NegativeSamplingLoss:
    def __init__(self, W, corpus, power=0.75, sample_size=5):
        self.sample_size = sample_size
        self.sampler = UnigramSampler(corpus, power, sample_size)
        self.loss_layers = [SigmoidWithLoss() for _ in range(sample_size + 1)]
        self.embed_dot_layers = [EmbeddingDot(W) for _ in range(sample_size + 1)]

        self.params, self.grads = [], []
        for layer in self.embed_dot_layers:
            self.params += layer.params
            self.grads += layer.grads

    def forward(self, h, target):
        batch_size = target.shape[0]
        negative_sample = self.sampler.get_negative_sample(target)

        # 正例的正向传播
        score = self.embed_dot_layers[0].forward(h, target)
        correct_label = np.ones(batch_size, dtype=np.int32)
        loss = self.loss_layers[0].forward(score, correct_label)

        # 负例的正向传播
        negative_label = np.zeros(batch_size, dtype=np.int32)
        for i in range(self.sample_size):
            negative_target = negative_sample[:, i]
            score = self.embed_dot_layers[1 + i].forward(h, negative_target)
            loss += self.loss_layers[1 + i].forward(score, negative_label)

        return loss

    def backward(self, dout=1):
        dh = 0
        for l0, l1 in zip(self.loss_layers, self.embed_dot_layers):
            dscore = l0.backward(dout)
            dh += l1.backward(dscore)

        return dh

二分类改进CBOW

解决问题二：中间层的神经元和权重矩阵的乘积、Softmax 层的计算需要花费很多计算时间

第k个单词的 Softmax 的计算式如下，其中Si是第i个单词的得分。这个计算也与词汇量成正比，所以需要一个替代Softmax的计算。

使用 Negative Sampling (负采样) 替代 Softmax。也就是用二分类拟合多分类。

多分类问题：从100万个单词中选择1个正确单词。

二分类问题：处理答案为是或否的问题，比如目标词是 say 吗。

让神经网络来回答：当上下文是 you 和 goodbye 时，目标词是 say 吗？

这时输出层只需要一个神经元，神经元输出的是 say 的得分。

仅计算目标词得分的神经网络如下。

上面这个图，中间层是one-hot 表示矩阵和权重矩阵的乘积，也就是权重矩阵的某个特定行。

当输出侧神经元只有一个的时候，计算中间层和输出侧的权重矩阵的乘积，只需要提取输出侧权重矩阵的某一列(目标词所在的列)，将提取的这一列与中间层进行内积计算。示意图如下图。

输出侧的权重矩阵中保存了各个单词ID对应的单词向量，提取目标词的单词向量，再求这个向量和中间层神经元 的内积，就是最终的得分。

多分类：输出层使用Softmax函数将得分转化为概率，损失函数使用交叉熵误差。

二分类：输出层使用sigmoid函数将得分转化为概率，损失函数使用交叉熵误差。

sigmoid 函数的输出可以解释为概率。

通过sigmoid函数得到概率后，可以由概率计算损失。

多分类交叉熵误差数学表达：yk是神经网络的输出，tk是正确解标签，k表示数据的维数。如果标签为one-hot表示，即tk中只有正确解标签索引为1，其他均为0 。那么式子只计算对应正确解标签的输出的自然对数。

二分类的交叉熵误差数学表达式：

y是sigmoid函数的输出(神经网络判断的目标词是say的得分)，t是正确解标签，t取值为1或0。t=1，输出-tlogy，求目标词是say情况下的损失。t=0，求目标词不是say情况下的损失。这个式子和多分类的其实是一回事：式子只计算对应标签的输出的自然对数。

Sigmoid层和Cross Entropy Error层的计算图如下。y是神经网络输出的概率，t是正确解标签。y-t相当于误差。误差向前面的层传播。误差大时，模型学习得多(参数的更新力度增大)。

举个例子，t=1，y接近1，误差就小。

正确解标签是1是什么意思，其实就是：正确答案就是这个词，神经网络输出的概率越接近于1，表示预测的越准确。

二分类的CBOW模型：向Sigmoid with Loss 层输入正确解标签1，表示现在正在处理的问题的答案是Yes。当答案是No时，向 Sigmoid with Loss 层输入0。

Embedding Dot 层合并Embedding 层和 dot 运算(内积运算)：

Embedding Dot 层实现代码如下：

成员变量：params保存参数，grads保存梯度。embed保存Embedding层，cache保存正向传播时的计算结果。

正向传播：参数接收中间层的神经元h，单词ID列表(idx)。首先调用Embedding层的forward(idx)方法，然后通过下面这种方式计算内积。

上面的例子，单词列表有3个数，表示mini-batch一并处理3个数据。

反向传播：乘法节点需要将上游传过来的导数dout乘正向传播的翻转值，然后传给下游。

class EmbeddingDot:
    def __init__(self, W):
        self.embed = Embedding(W)
        self.params = self.embed.params
        self.grads = self.embed.grads
        self.cache = None

    def forward(self, h, idx):
        target_W = self.embed.forward(idx)
        out = np.sum(target_W * h, axis=1)

        self.cache = (h, target_W)
        return out

    def backward(self, dout):
        h, target_W = self.cache
        dout = dout.reshape(dout.shape[0], 1)

        dtarget_W = dout * h
        self.embed.backward(dtarget_W)
        dh = dout * target_W
        return dh

目前，只是对正例say进行了二分类，如果此时模型有好的权重，则Sigmoid层的输出概率将接近1。

真正要做的事是，对于正例say，使Sigmoid层的输出接近1；对于负例(say 以外的单词)，使Sigmoid层的输出接近0。

权重需要满足：当输入say时使Sigmoid层的输出接近1，当输入say以外的单词时使输出接近0。如下图，当上下文是 you和goodbye时，目标词是hello（错误答案）的概率要比较低。