nlp skip gram模型

skip gram模型的实现

CBOW模型的概率表示：

P(A)：A发生的概率。

P(A,B)：事件A和事件B同时发生的概率，称为联合概率。

P(A|B)：在给定事件B的信息后，事件A发生的概率，称为后验概率。

CBOW模型：当给定某个上下文时，输出目标词的概率。

用数学式来表示给定上下文wt-1和wt+1时目标词为wt的概率：

交叉熵误差函数公式：yk是神经网络的输出， tk是正确解标签， k表示数据的维数。如果标签为one-hot表示，即tk中只有正确解标签索引为1，其他均为0 。那么式子只计算对应正确解标签的输出的自然对数。

CBOW 模型的损失函数（一 笔样本数据的损失函数）：

CBOW 模型的损失函数（扩展到整个语料库）：

CBOW 模型学习的任务：让上面损失函数尽可能地小。那时的权重参数就是想要的单词的分布式表示。（这里只考虑窗口大小为 1 的情况）

skip-gram 模型：CBOW 模型从上下文的多个单词预测中间的单词（目标词），而 skip-gram 模型则从中间的单词（目标词）预测周围的多个单词（上下文）。

skip-gram 模型的网络结构：输入层只有一个，输出层的数量则与上下文的单词个数相等。要分别求出各个输出层的损失（通过 Softmax with Loss 层等），然后将它们加起来作为最后的损失。

skip-gram 模型的数学表示：

在 skip-gram 模型中，假定上下文的单词之间出现的条件独立。

代入交叉熵误差函数，可以推导出 skip-gram 模型一笔样本数据的损失函数。skip- gram 模型的损失函数先分别求出各个上下文对应的损失，然后将它们加在一 起。

扩展到整个语料库， skip-gram 模型的损失函数可以表示为：

skip-gram在准确度上比CBOW高。CBOW 模型比 skip-gram 模型学习速度要快。

skip-gram 模型的实现：

import sys
sys.path.append('..')
import numpy as np
from common.layers import MatMul, SoftmaxWithLoss


class SimpleSkipGram:
    def __init__(self, vocab_size, hidden_size):
        V, H = vocab_size, hidden_size

        # 初始化权重
        W_in = 0.01 * np.random.randn(V, H).astype('f')
        W_out = 0.01 * np.random.randn(H, V).astype('f')

        # 生成层
        self.in_layer = MatMul(W_in)
        self.out_layer = MatMul(W_out)
        self.loss_layer1 = SoftmaxWithLoss()
        self.loss_layer2 = SoftmaxWithLoss()

        # 将所有的权重和梯度整理到列表中
        layers = [self.in_layer, self.out_layer]
        self.params, self.grads = [], []
        for layer in layers:
            self.params += layer.params
            self.grads += layer.grads

        # 将单词的分布式表示设置为成员变量
        self.word_vecs = W_in

    def forward(self, contexts, target):
        h = self.in_layer.forward(target)
        s = self.out_layer.forward(h)
        l1 = self.loss_layer1.forward(s, contexts[:, 0])
        l2 = self.loss_layer2.forward(s, contexts[:, 1])
        loss = l1 + l2
        return loss

    def backward(self, dout=1):
        dl1 = self.loss_layer1.backward(dout)
        dl2 = self.loss_layer2.backward(dout)
        ds = dl1 + dl2
        dh = self.out_layer.backward(ds)
        self.in_layer.backward(dh)
        return None

调用这个skip-gram模型

# coding: utf-8
import sys
sys.path.append('..')  # 为了引入父目录的文件而进行的设定
from common.trainer import Trainer
from common.optimizer import Adam
#from simple_cbow import SimpleCBOW
from simple_skip_gram import SimpleSkipGram
from common.util import preprocess, create_contexts_target, convert_one_hot


window_size = 1
hidden_size = 5
batch_size = 3
max_epoch = 1000

text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)

vocab_size = len(word_to_id)
contexts, target = create_contexts_target(corpus, window_size)
target = convert_one_hot(target, vocab_size)
contexts = convert_one_hot(contexts, vocab_size)

#model = SimpleCBOW(vocab_size, hidden_size)
model = SimpleSkipGram(vocab_size, hidden_size)
optimizer = Adam()
trainer = Trainer(model, optimizer)

trainer.fit(contexts, target, max_epoch, batch_size)
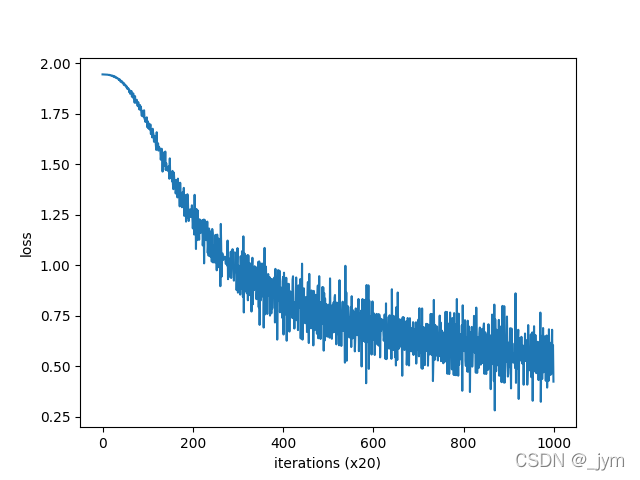
trainer.plot()

word_vecs = model.word_vecs
for word_id, word in id_to_word.items():
    print(word, word_vecs[word_id])

you [ 0.0070119   0.01140655 -0.00602617 -0.00951831  0.00306297]
say [ 0.90311    -0.90883684  0.92998946  0.9578707   1.1098603 ]
goodbye [-0.8135963   0.805687   -0.8332484  -0.86875284  1.1370432 ]
and [ 0.9542584  -0.9512509   0.97993344  0.98317575 -1.2883114 ]
i [-0.80985945  0.81495476 -0.85571784 -0.84448576  1.1391366 ]
hello [-0.8404988  0.8455065 -0.8266616 -0.8118625 -1.3357102]
. [-0.01073505 -0.01199387 -0.02076071 -0.01374857  0.01593136]

对比一下之前的CBOW模型的输出：发现两个方法得到的单词的密集向量的表示有很大不同。

you [-0.9987413   1.0136298  -1.4921554   0.97300434  1.0181936 ]
say [ 1.161595   -1.1513934  -0.25779223 -1.1773298  -1.1531342 ]
goodbye [-0.88470864  0.9155085  -0.30859873  0.9318609   0.9092796 ]
and [ 0.7929211 -0.8148116 -1.8787507 -0.7845257 -0.8028278]
i [-0.8925459   0.95505357 -0.29667985  0.90895575  0.90703803]
hello [-1.0259517   0.97562104 -1.5057516   0.96239203  1.0297285 ]
. [ 1.2134467 -1.1766206  1.6439314 -1.1993438 -1.1676227]