机器学习 卷积神经网络
2022-04-05 14:27 jym蒟蒻 阅读(132) 评论(0) 收藏 举报卷积神经网络的整体结构、卷积层、池化、python实现
- 一、整体结构
- 二、卷积层
- 三、池化层
- 四、python实现卷积层、池化层
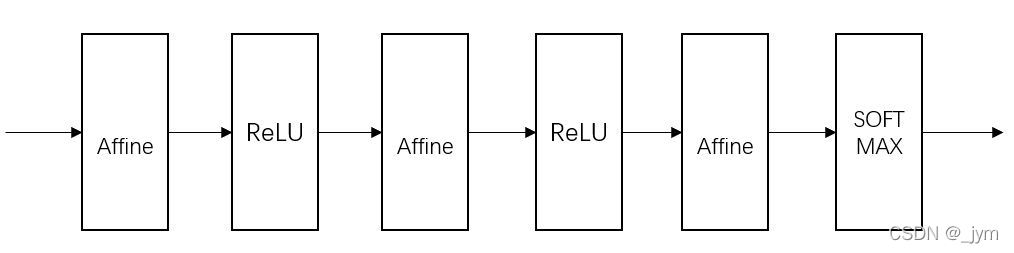
神经网络相邻层所有神经元之间都有连接,称为全连接。前面用Affine层实现了全连接。
举个例子
全连接神经网络结构:
卷积神经网络CNN的结构:
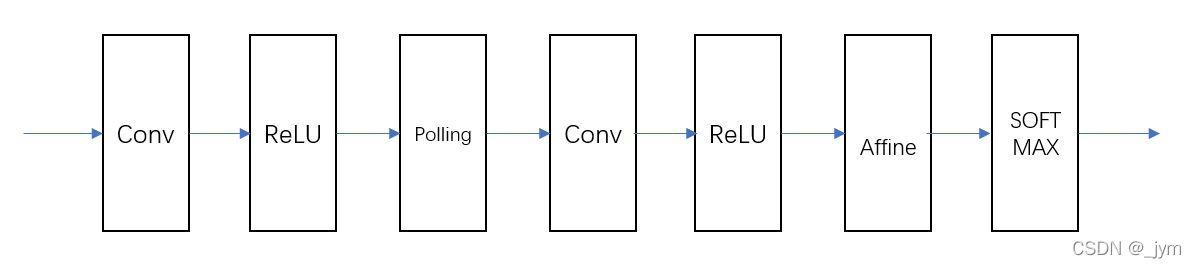
新增了Conv卷积层和Pooling池化层,之前的Affine-ReLU连接替换成了Conv-ReLU-Pooling连接。
CNN中,靠近输出的层中使用之前Affine-ReLU组合,最后输出层使用之前Affine-softmax组合,这是一种常见的CNN结构。
全连接神经网络存在的问题就是数据的形状被忽视了,输入三维图像,但是向全连接层输入时,需将三维拉成一维,这导致忽视了形状中含有的空间信息,也就是说全连接,无法利用与形状相关的信息。
卷积神经网络为了解决这一问题,向各层中传递的数据是有形状的数据,比如三维数据。
卷积层进行卷积运算,就像是图像处理的滤波。
对于输入数据,卷积运算以一定间隔滑动滤波器的窗口并将各个位置上滤波器的元素和输入的对应元素相乘再求和,进行所谓乘积累加运算。
全连接神经网络中,参数有权重和偏置等。
CNN中滤波器里面的数就是参数,滤波器里面数据的偏置也是参数。要通过cnn网络对数据的学习,把这些参数给找到,从而达到优异的学习效果。
有时候进行卷积处理前要进行填充,也就是向输入数据周围填入固定的数据,填充主要是为了调整输出的大小。(4,4)的输入数据应用(3,3)滤波器时,输出为(2,2),输出比输入缩小两个元素就导致一个问题,如果每次进行卷积运算都缩小输出,那么某时刻就无法再对输出进行卷积运算,网络就传不下去了。如果说这个例子填充幅度是1,那么卷积运算输出也是(4,4),卷积运算就可以在保持空间大小不变的情况下传递数据给下一层。
增大步幅,输出大小会变小,增大填充输出大小会变大。
假设输入大小为(H,W),滤波器大小为(FH,FW),输出大小为(OH,OW),填充为P,步幅为S。
有下面这个公式。
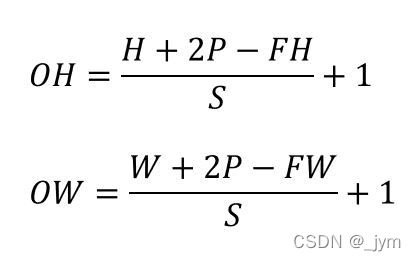
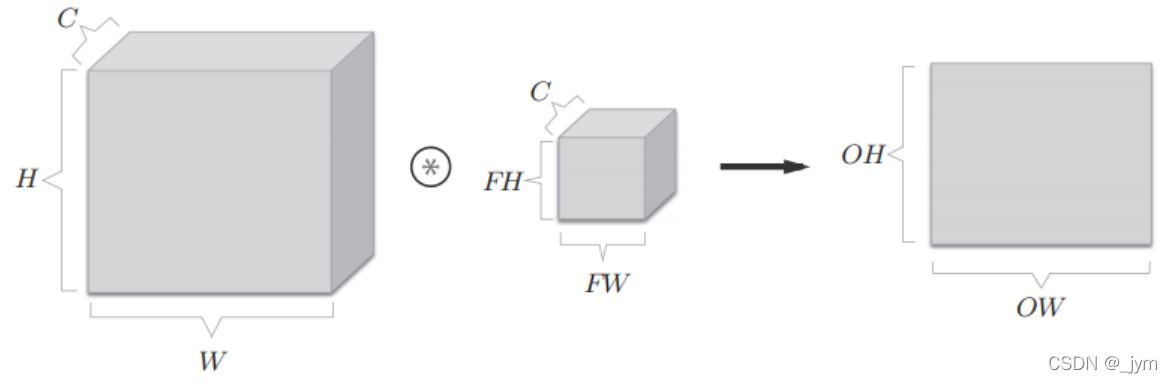
多维数据的卷积运算:
通道数为C、高度为H、长度为W的数据形状,(C,H,W)
滤波器通道数为C、高度为FH、长度为FW,(C,FH,FW)
卷积后输出的是一张特征图。可以这样理解,一个小方块在大方块里面移动,由于大方块的C和小方块一样,所以卷积后是二维的。
如果想在通道上也有多个卷积运算,就需要用到多个滤波器如下图。输出将以方块的形式传给下一层。
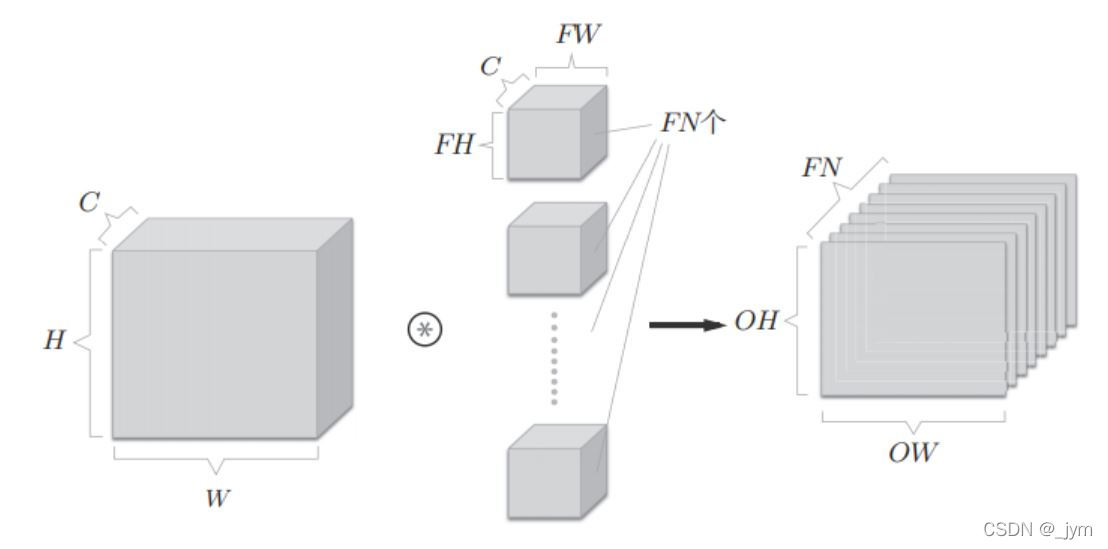
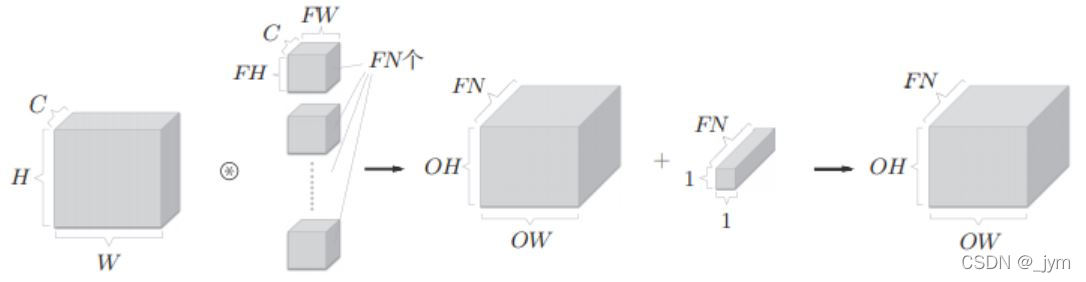
如果增加偏置,如下图:小长方体,也就是FN个偏置值。
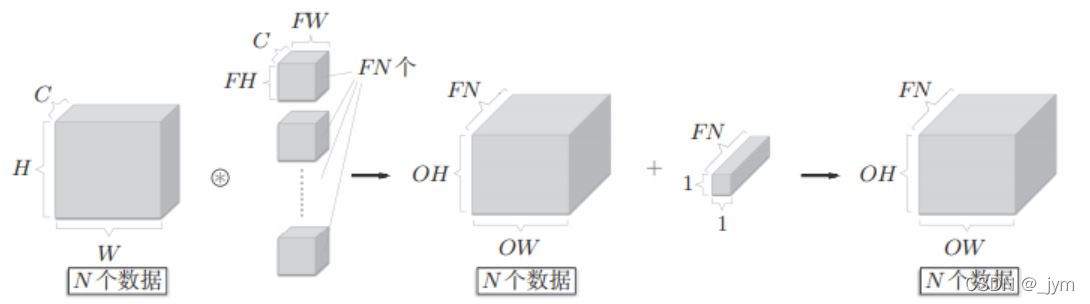
如果增加批处理,也就是一次性处理N个数据,那么各层传递数据保存维度将增加一维,如下图。
池化是缩小高、长方向上的空间运算。Max池化层是获取目标区域最大值,然后把最大值放到输出数据的其中一个元素里。池化层没有要学习的参数,通道数不发生变化。池化对输入数据微小偏差具有鲁棒性,也就是说,输入数据发生微小偏差时,池化层返回(与输入数据没发生微小偏差时)相同的输出结果。
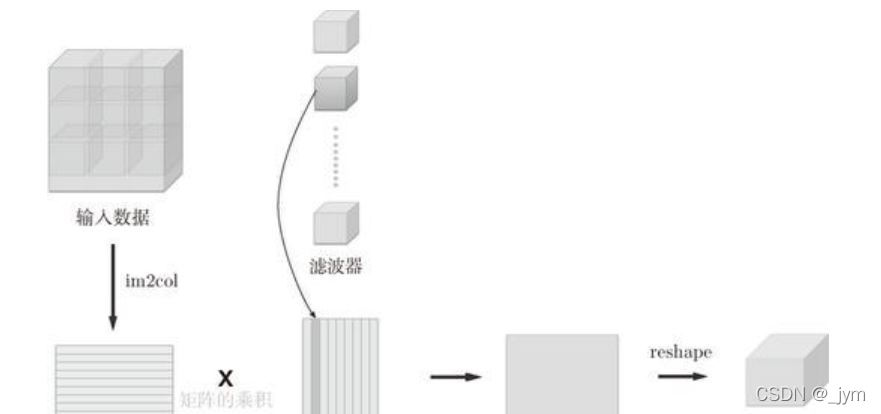
对于卷积来说,im2col这个函数能够把大方块的小方块展开一行,这样的话能和滤波器的小方块 进行矩阵乘积运算,如下图所示。
对于池化来说,im2col依然可以这么展开,就是把大正方形里面的小正方形展成一行,这里就不放图了。
im2col实现代码:
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
input_data : 由(数据量, 通道, 高, 长)的4维数组构成的输入数据
filter_h : 滤波器的高
filter_w : 滤波器的长
stride : 步幅
pad : 填充
Returns
-------
col : 2维数组
"""
N, C, H, W = input_data.shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
反向传播时候,要进行im2col逆处理,用的是col2im函数。
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
col :
input_shape : 输入数据的形状(例:(10, 1, 28, 28))
filter_h :
filter_w
stride
pad
Returns
-------
"""
N, C, H, W = input_shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)
img = np.zeros((N, C, H + 2*pad + stride - 1, W + 2*pad + stride - 1))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]
return img[:, :, pad:H + pad, pad:W + pad]
卷积层、池化层实现代码:
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
# 中间数据(backward时使用)
self.x = None
self.col = None
self.col_W = None
# 权重和偏置参数的梯度
self.dW = None
self.db = None
def forward(self, x):
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
out_h = 1 + int((H + 2*self.pad - FH) / self.stride)
out_w = 1 + int((W + 2*self.pad - FW) / self.stride)
col = im2col(x, FH, FW, self.stride, self.pad)
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
self.x = x
self.col = col
self.col_W = col_W
return out
def backward(self, dout):
FN, C, FH, FW = self.W.shape
dout = dout.transpose(0,2,3,1).reshape(-1, FN)
self.db = np.sum(dout, axis=0)
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
dcol = np.dot(dout, self.col_W.T)
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
self