机器学习 反向传播 实现神经网络的ReLU、Sigmoid激活函数层

结合反向传播算法使用python实现神经网络的ReLU、Sigmoid激活函数层

这里写目录标题

• 一、ReLU层的实现
• 二、Sigmoid层的实现
• 三、实现神经网络的Affine层
• 四、Softmax-with-Loss层实现

 

一、ReLU层的实现

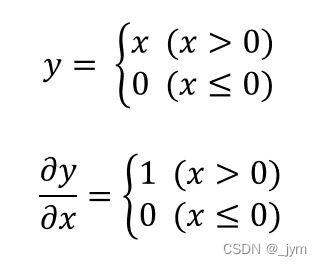
正向传播时的输入大于0，则反向传播会将上游的值原封不动地传给下游，这是因为y对x偏导是1，而传出来的数又是输入乘以偏导，那么输出就是上游的值。

如果正向传播时的x小于等于0，则反向传播中传给下游的信号将停在此处。因为偏导是0，所以输入乘偏导就等于0，输出就是0。

代码实现：这个里面forward和backward参数是Numpy数组。

mask是由True和False构成的Numpy数组，会把正向传播输入x元素中，<=0的地方保存为True，>0的保存为False。反向传播中会使用正向传播时保存的mask，将dout的mask中元素为true地方设为0。

out[self.mask] = 0，这句话是说，mask为true的地方设为0。

class Relu:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0

        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout

        return dx

二、Sigmoid层的实现

最后一个节点那块，进行的是y=1/x的操作，求y关于x的偏导，最后用y表示出来，（因为反向传播是倒着的，所以要用y表示）。

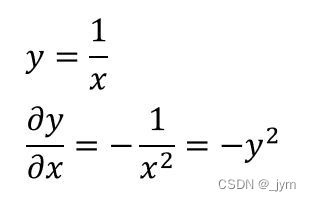
代码：

out保存正向传播的输出，反向传播时候，用out计算。变量都是Numpy数组。

class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = sigmoid(x)
        self.out = out
        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out

        return dx

三、实现神经网络的Affine层

神经网络正向传播计算加权信号综合，使用矩阵的乘积运算。

Y=np.dot(X,W)+B

正向进行的矩阵乘积运算，称为仿射变换，Affine。

输入X是单个数据时的反向传播图如图所示：

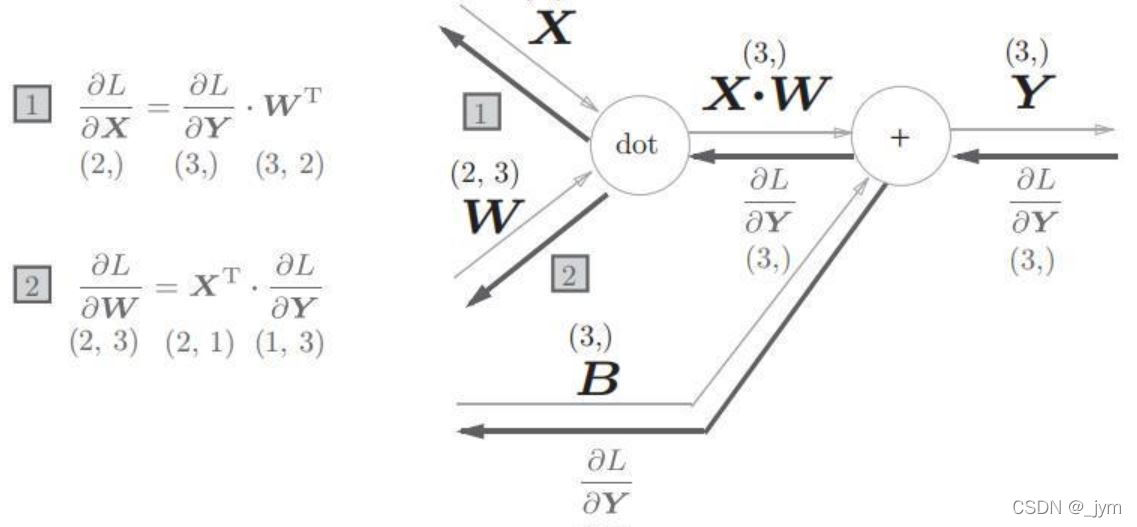
输入X是N个数据时：

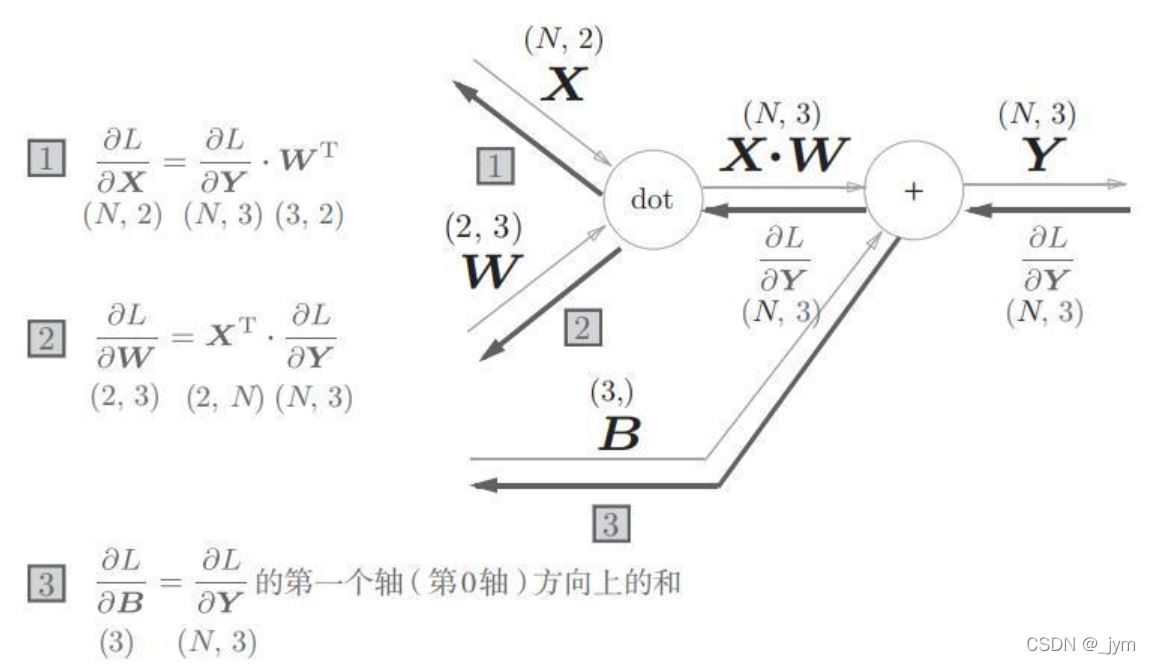
代码：

以后有时间再来分析。

class Affine:
    def __init__(self, W, b):
        self.W =W
        self.b = b
        
        self.x = None
        self.original_x_shape = None
        # 权重和偏置参数的导数
        self.dW = None
        self.db = None

    def forward(self, x):
        # 对应张量
        self.original_x_shape = x.shape
        x = x.reshape(x.shape[0], -1)
        self.x = x

        out = np.dot(self.x, self.W) + self.b

        return out

    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        
        dx = dx.reshape(*self.original_x_shape)  # 还原输入数据的形状（对应张量）
        return dx

四、Softmax-with-Loss层实现

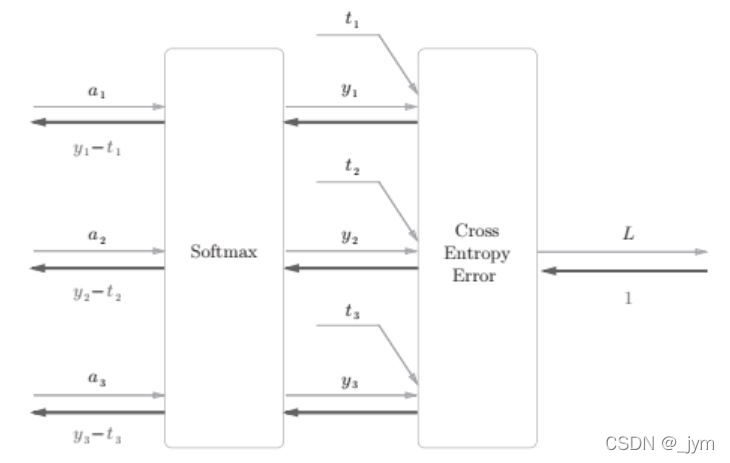
交叉熵误差作为Softmax函数的损失函数后，反向传播得到y1-t1之类的结果，这是差分表示的误差，说明神经网络的反向传播会把误差传递给前面的层。

这样结果不偶然，使用平方和误差作为恒等函数的损失函数，交叉熵误差作为Softmax函数的损失函数，反向传播才能够得到y1-t1之类的结果。

代码：

以后有时间再来分析。

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None # softmax的输出
        self.t = None # 监督数据

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        
        return self.loss

    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        if self.t.size == self.y.size: # 监督数据是one-hot-vector的情况
            dx = (self.y - self.t) / batch_size
        else:
            dx = self.y.copy()
            dx[np.arange(batch_size), self.t] -= 1
            dx = dx / batch_size
        
        return dx