义乌集训7.11 contest 4题解
2021.7.11 Contest 题解
T1:
Description:
有 \(n\) 只青蛙,第 \(i\) 只青蛙会每过 \(x_i\) 秒会连续叫 \(y_i\) 秒。然而由于青蛙的寿命在增加,所以从第二次开始每次休息结束后这只青蛙连续叫的时间会增加 \(z_i\) 秒。
给定 \(n\) 只青蛙,每一只的 \(x_i,y_i,z_i\),以及时间 \(t\),求在前 \(t\) 秒中,所有青蛙共叫了多少秒。
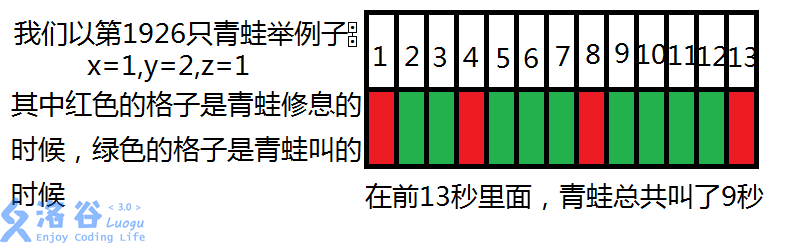
Input:
第一行两个数 \(n\) 和 \(t\)。
之后 \(n\) 行,第 \(i+1\) 行每行三个非负整数 \(x_i,y_i,z_i\)。
Output:
一行一个数表示答案。
Sample1 Input:
8 10
9 1 1
1 9 9
4 1 0
2 3 3
1 0 0
1 4 0
9 2 5
1 2 1
Sample1 Output:
34
Sample2 Input:
1 233333
233 233 233
Sample2 Output:
223081
Sample3 Input:
10 100000000
1 0 0
1 0 5
1 2 2
1 2 8
1 3 0
1 5 0
1 5 2
1 5 5
1 7 0
1 8 3
Sample3 Output:
845787522
Hint:
样例 #4,#5 见下发的文件
子任务会给出部分测试数据的特点。 如果你在解决题目中遇到了困难, 可以尝试只解决一部分测试数据。
每个测试点的数据规模及特点如下表:
| 测试点编号 | n的范围 | t的范围 | 特殊性质 |
|---|---|---|---|
| \(1\) | \(n = 1\) | ||
| \(2\) | \(n = 100\) | \(t \le 100\) | \(x = 0\) |
| \(3\) | \(n = 100\) | \(y = 0\) | |
| \(4\) | \(n = 100\) | \(z = 0\) | |
| \(5\) | \(n = 100\) | ||
| \(6\) | \(n = 100000\) | \(t\le 100\) | \(x = y = z\) |
| \(7\) | \(n = 100000\) | \(t\le 100\) | \(z = 0\) |
| \(8\) | \(n = 100000\) | \(y = 0\) | |
| \(9\) | \(n = 100000\) | \(t\le 100000\) | |
| \(10\) | \(n = 100000\) |
对于 \(100\%\) 的数据,\(n \le 100000 , t \le 2000000000,x + y + z > 0\),\(0 \le x , y , z \le 2000000000\)。
【说明】
【样例 \(1\) 说明】
每只青蛙分别叫了 \(1,9,2,6,0,8,1,7\) 秒。
【样例 \(2\) 说明】
那只青蛙叫了 \(223081\) 秒。
【样例 \(3\) 说明】
每只青蛙分别叫了\(0,99993675,99990000,99994999,75000000,83333333,99990002,99993676,87500000,99991837\) 秒。
题目分析:
推个柿子,二分一下然后算答案即可。无非就是个等差数列求和。
代码如下(马蜂很丑,不喜勿喷)——
#include<bits/stdc++.h>
#define N 500005
#define LL long long
using namespace std;
int n;LL ans,t;
inline int read(){
int ret=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}
while(isdigit(ch)) ret=(ret<<1)+(ret<<3)+ch-'0',ch=getchar();return ret*f;
}
int main(){
freopen("a.in","r",stdin);freopen("a.out","w",stdout);
n=read(),t=read();while(n--){
LL x=read(),y=read(),z=read(),l=0,r=t,T=-1;if(z) r=min(r,(LL)sqrt(2ll*t/z));while(l<=r)
{LL mid=l+r>>1ll;if(1ll*(mid+1)*(x+y)+1ll*mid*(mid+1)/2ll*z<=t) l=mid+1,T=mid;else r=mid-1;}
LL res=(T+1)*y+1ll*T*(T+1)/2ll*z,tt=t-(T+1)*(x+y)-1ll*T*(T+1)/2ll*z;if(tt>x) res+=tt-x;ans+=(LL)res;
}
cout<<ans<<'\n';return 0;
}
T2:
Description:
有一款垃圾游戏叫坦克世界,也叫作脚本世界。
坦克有各种炮弹,比如 AP,APC,APCBC,APCR,APCNR,APBC,APDS,APFSDS,HEAT,HEATFS,HE,HESH,HVAP......
其实我也只认得其中一部分。
为了简化游戏,我们只考虑全口径穿甲弹 AP (Armor Piercing) 与高爆榴弹 HE (High Explosive)。
每种炮弹有一个标准伤害值,当炮弹击中敌人,会由以下方法计算伤害:
AP : 如果击穿了敌人的装甲,则敌人会受到该炮弹的标准伤害值大小的伤害,如果我们未能击穿敌人的装甲,则敌人不受到任何伤害。
HE : 如果击穿了敌人的装甲,则敌人会受到该炮弹的标准伤害值大小的伤害,如果我们未能击穿敌人的装甲,则敌人会受到一个在 \([0,0.5 \times \mathrm{标准伤害值}]\) 中均匀随机的整数伤害值。
游戏有一个特性,因为 HE 炮弹的装药一般都比 AP 多(要是比 AP 还少那实在是没救了),所以 HE 炮弹的标准伤害值大于 AP 炮弹的标准伤害值。
在上一局游戏中,nzhtl1477 发射了 \(n\) 发炮弹,但是不知道这些炮弹是否有击穿敌人或者击中敌人,请问该玩家是否可能造成了总共 \(m\) 点伤害?
Input:
输入包含多组数据,第一行输入一个 \(t\) 表示数据组数。
之后 \(t\) 行,每行四个数 \(n, m, a, b\) ,其中 \(n,m\) 的意义如上述,\(a\) 表示 AP 的标准伤害值,\(b\) 表示 HE 的标准伤害值。
保证 \(a<b\),\(a\) 与 \(b\) 均为正整数,所有数均为整数。
Output:
输出 \(t\) 行,对每组数据,如果可以,输出 "Yes",否则输出 "No"(均不带括号)。
Sample1 Input:
10
1 3 4 5
1 4 4 5
1 5 4 5
2 7 4 5
2 8 4 5
2 9 4 5
2 10 4 5
2 11 4 5
114 514 2 4
114 514 2 5
Sample1 Output:
No
Yes
Yes
Yes
Yes
Yes
Yes
No
No
Yes
Hint:
对于 \(30\%\) 的数据,满足 \(t\le 10\), \(0\le n,m,a,b\le 10^5\)。
对于另外 \(30\%\) 的数据,满足 \(t\le 100\)。
对于 \(100\%\) 的数据,满足 \(1 \leq t \leq 10 ^ 6\),\(0 \leq n,m \leq 10 ^ {18}\),\(1 \leq a<b \leq 10 ^ {18}\)。
题目分析:
小清新结论题。如果 \(b\times n \leq m\),显然不成立,直接退出。在此基础上:
若 \(m\) 是 \(b\) 的倍数,则成立;
若 \(m \% b \leq b/2\) ,即可以通过使用若干个HE击穿装甲再用 \(1\) 个HE不击穿装甲但产生贡献,成立;
若 \(n-m/b \geq 2\),即使用若干个HE击穿装甲直到 \(m < b\) 时,还剩余 \(2\) 个以上的炮弹,肯定可以用 \(2\) 个不击穿装甲的HE凑出 \(m\),成立;
此时我们仅需考虑剩余 \(1\) 发炮弹,且剩余伤害值 \(> b/2\) 的情况。
那么我们采取用AP替换HE的策略直到剩余伤害值恰好等于 \(a\),则设替换的个数等于 \(z\),剩余的伤害值为 y,已用的炮弹数为 \(x\)。
\(z*(b-a)=a-y\) 且 \(0 \leq z \leq x\),能找到满足条件的 \(z\) ,则成立;反之,不成立。
如果你像我一样写了龟速乘来判断 \(b \times n\) 是否 \(\geq m\) 注意 \(n=0\) 的情况。(主要是我的写法有小问题QAQ)
代码如下(马蜂很丑,不喜勿喷)——
#include<bits/stdc++.h>
#define N 200005
#define LL long long
using namespace std;
int T;LL n,m,a,b;
inline bool mul(LL x,LL y,LL z){LL res=0;while(y){if(y&1ll) res+=x;if(res>=z) return 1;y>>=1ll,x<<=1ll;if(y&&x>=z) return 1;}if(res<z) return 0;return 1;}
inline LL read(){
LL ret=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}
while(isdigit(ch)) ret=(ret<<1ll)+(ret<<3ll)+ch-'0',ch=getchar();return ret*f;
}
int main(){
freopen("b.in","r",stdin);freopen("b.out","w",stdout);
T=read();while(T--){
n=read(),m=read(),a=read(),b=read(); if(!mul(b,n,m)){puts("No");continue;}
if(m%b==0){puts("Yes");continue;} LL x=m/b,y=m%b;if(y<=b/2){puts("Yes");continue;}
if(n-x>=2){puts("Yes");continue;} if((a-y)%(b-a)==0){LL z=(a-y)/(b-a);if(z>=0&&z<=x){puts("Yes");continue;}} puts("No");
}
return 0;
}
T3:
Description:
给你一个图,保证每个点最多属于一个简单环,每个点度数最多为 \(3\),求这个图有多少“眼镜图形”。
其中“眼镜图形”,定义为三元组 \((x,y,S)\),其中 \(x\) 和 \(y\) 表示图上的两个点,\(S\) 表示一条 \(x\) 到 \(y\) 的简单路径,而且必须满足:
-
\(x\) 和 \(y\) 分别在两个不同的简单环上
-
\(x\) 所在的简单环与路径 \(S\) 的所有交点仅有 \(x,y\) 所在的简单环与路径S的所有交点仅有 \(y\)。
\((x,y,S)\) 与 \((y,x,S)\) 算同一个眼镜。
如果你无法理解,可以参考样例。
保证图是联通的
Input:
第一行两个数 \(n\) 和 \(m\)。
之后 \(m\) 行,每行两个数 \(x,y\) 表示 \(x\) 和 \(y\) 之间有一条边。
Output:
输出一个数,表示眼镜的个数对 \(19260817\) 取膜的结果。
Sample1 Input:
11 12
1 2
2 3
3 4
4 5
5 1
4 6
6 7
7 8
8 9
9 10
10 11
11 7
Sample1 Output:
1
Sample2 Input:
14 16
1 2
2 3
3 4
4 1
3 5
5 6
6 7
7 8
8 9
9 6
9 13
13 14
13 10
10 11
11 12
12 10
Sample2 Output:
4
Hint:
样例 #3,#4,#5,#6 见下发的文件
子任务会给出部分测试数据的特点。
如果你在解决题目中遇到了困难, 可以尝试只解决一部分测试数据。
| 测试点编号 | n的范围 | m的范围 | 特殊性质 |
|---|---|---|---|
| \(1\) | \(n \le 10\) | \(m \le 20\) | |
| \(2\) | \(n \le 20\) | \(m \le 40\) | |
| \(3\) | \(n \le 20\) | \(m \le 40\) | |
| \(4\) | \(n \le 2000\) | \(m \le 4000\) | |
| \(5\) | \(n \le 2000\) | \(m \le 4000\) | |
| \(6\) | \(n \le 1000000\) | \(m \le 2000000\) | 简单环个数$ \le 2000$ |
| \(7\) | \(n \le 1000000\) | \(m \le 2000000\) | 简单环个数$ \le 2000$ |
| \(8\) | \(n \le 1000000\) | \(m \le 2000000\) | |
| \(9\) | \(n \le 1000000\) | \(m \le 2000000\) | |
| \(10\) | \(n \le 1000000\) | \(m \le 2000000\) |
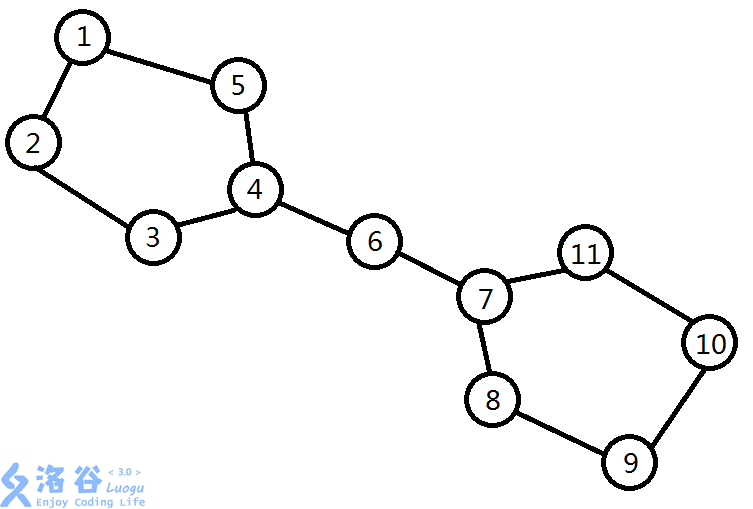
【样例 \(1\)说明】
有 \((4,5,1,2,3)—6—(7,8,9,10,11)\) 这一个眼镜
【样例 \(2\) 说明】
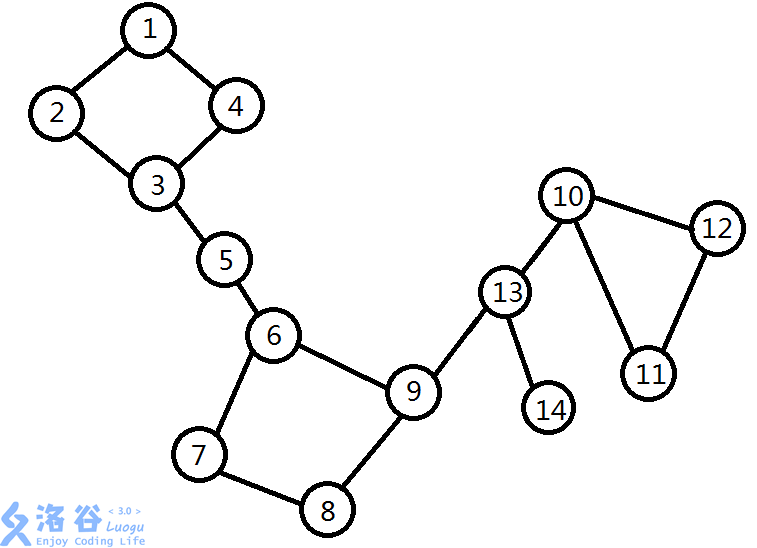
有四个眼镜,下图中分别标出:
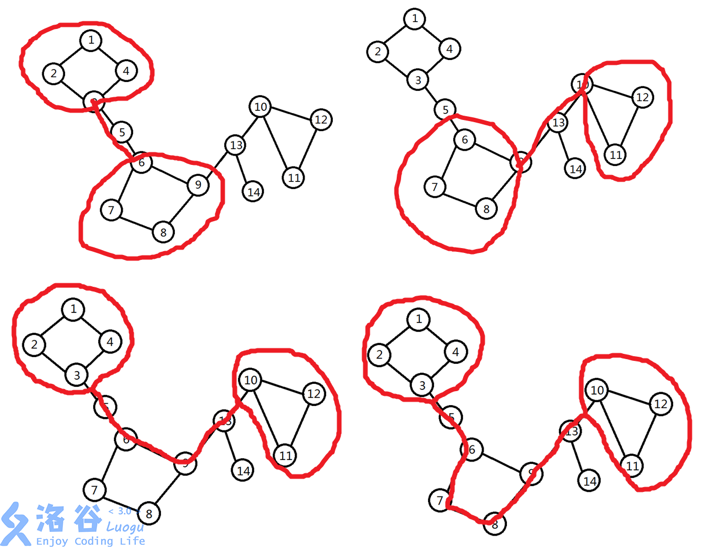
题目分析:
首先找到环,缩点之后根据给定的图的性质跑树形DP,做法比较套路,有些小细节需要注意。
代码如下(马蜂很丑,不喜勿喷)——
#include<bits/stdc++.h>
#define N 2000005
#define LL long long
using namespace std;
int n,m,ans,tot=1,H,top,u[N],v[N],f[N],st[N],B[N],fir[N],nxt[N<<1],son[N<<1];const int p=19260817;bool vis[N];
inline void add(int x,int y){son[++tot]=y,nxt[tot]=fir[x],fir[x]=tot;} inline void dfs(int x,int fa)
{vis[x]=1,st[++top]=x;for(register int i=fir[x];i;i=nxt[i]) if(fa!=(i^1)) if(vis[son[i]]){int to=son[i];if(B[to]) continue;tot++;while(st[top]^to) B[st[top]]=tot,top--;B[to]=tot,top--;} else dfs(son[i],i);if(st[top]==x) top--;}
inline void solve(int x,int fa){for(register int i=fir[x];i;i=nxt[i]) if(son[i]^fa){int to=son[i];solve(to,x),ans+=1ll*f[x]*(f[to]*(to<=H?2:1)+(to<=H))*(x<=H?2:1)%p,(ans>=p)&&(ans-=p),f[x]+=f[to]*(to<=H?2:1)+(to<=H),f[x]%=p;} if(x<=H) ans+=f[x],(ans>=p)&&(ans-=p);}
inline int read(){int ret=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}while(isdigit(ch)) ret=(ret<<1)+(ret<<3)+ch-'0',ch=getchar();return ret*f;}
int main(){
freopen("c.in","r",stdin);freopen("c.out","w",stdout);
n=read(),m=read();for(register int i=1;i<=m;i++) u[i]=read(),v[i]=read(),add(u[i],v[i]),add(v[i],u[i]);tot=0,dfs(1,-1),H=tot;for(register int i=1;i<=n;i++) if(!B[i]) B[i]=++tot;
memset(fir,0,sizeof(fir)),tot=0;for(register int i=1;i<=m;i++) if(B[u[i]]^B[v[i]]) add(B[u[i]],B[v[i]]),add(B[v[i]],B[u[i]]);solve(1,0),cout<<ans<<'\n';return 0;
}
T4:
Description:
给出三个长度 \(n\) 的正整数序列 \(A,B,C\)。
定义 \(f(X,l,r)\) 为在序列 \(X\) 中,区间 \([l,r]\) 的最大值减去区间 \([l,r]\) 的最小值的差。
定义一个区间 \([l,r]\) 的权值为 \(f(A,l,r)\times f(B,l,r)\times f(C,l,r)\)。
求对于所有 \(1\le l\le r\le n\),区间 \([l,r]\) 的权值之和,由于答案可能比较大,所以输出答案对 \(2^{32}\) 取模的结果。
Input:
第一行一个整数 \(n\)。
之后三行,每行 \(n\) 个正整数,分别表示 \(A,B,C\) 三个序列。
Output:
一行一个数表示答案。
Sample1 Input:
5
1 3 5 5 5
2 3 2 1 2
3 5 5 3 5
Sample1 Output:
60
Hint:
对于 \(20\%\) 的数据,满足 \(1\le n\le 2\times 10^3\)。
对于另外 \(20\%\) 的数据,满足 \(A,B,C\) 序列分别单调不减。
对于另外 \(10\%\) 的数据,满足 \(A\) 序列均为 \(1\)。
对于 \(100\%\) 的数据,满足 \(1\le n\le 10^5\),\(1\le A_i,B_i,C_i\le 10^9\)。
题目分析:
正解貌似是线段树+扫描线,但是方老师想了一种分治的做法。
首先答案可以直接把多项式打开,拆成 \(8\) 个贡献之和。
对于一段区间 \([l,r]\) 的贡献,我们可以找到一个分段点 \(mid\),于是贡献拆分成了 \([l,mid],[mid+1,r]\) 和跨过 \(mid\) 的区间的贡献。
前两段贡献递归处理,对于第三种贡献我们枚举 \(i\) \((l\leq i \leq mid)\) , 对于 \(j\) \((mid+1\leq j \leq r)\) 可以分成三段贡献,分类讨论一下做个前缀和之类的东西就能计算了。详情见代码。
代码如下(马蜂很丑,不喜勿喷)——
#include<bits/stdc++.h>
#define N 1000005
#define inf 1000000001
#define max(a,b) (a)>(b)?(a):(b)
#define uint unsigned int
using namespace std;
int n;uint ans,a[N],b[N],c[N],ax[N],bx[N],cx[N],sa[N],sb[N],sc[N],ab[N],ac[N],bc[N],abc[N];
inline void solve(int l,int r){
if(l>r) return;if(l==r) return;int mid=l+r>>1;solve(l,mid-1),solve(mid+1,r);int A=mid,B=mid,C=mid;uint aa=a[mid],bb=b[mid],cc=c[mid];
ax[mid-1]=bx[mid-1]=cx[mid-1]=ab[mid-1]=ac[mid-1]=bc[mid-1]=abc[mid-1]=sa[mid-1]=sb[mid-1]=sc[mid-1]=0;for(register int i=mid;i<=r;i++)
ax[i]=max(ax[i-1],a[i]),bx[i]=max(bx[i-1],b[i]),cx[i]=max(cx[i-1],c[i]),sa[i]=sa[i-1]+ax[i],sb[i]=sb[i-1]+bx[i],sc[i]=sc[i-1]+cx[i],
ab[i]=ab[i-1]+ax[i]*bx[i],ac[i]=ac[i-1]+ax[i]*cx[i],bc[i]=bc[i-1]+bx[i]*cx[i],abc[i]=abc[i-1]+ax[i]*bx[i]*cx[i];for(register int i=mid;i>=l;i--){
aa=max(aa,a[i]),bb=max(bb,b[i]),cc=max(cc,c[i]);while(ax[A]<=aa&&A<=r) A++;while(bx[B]<=bb&&B<=r) B++;while(cx[C]<=cc&&C<=r) C++;
if(A<=B&&B<=C) ans+=aa*bb*cc*(A-mid)+bb*cc*(sa[B-1]-sa[A-1])+cc*(ab[C-1]-ab[B-1])+abc[r]-abc[C-1];
else if(A<=C&&C<=B) ans+=aa*bb*cc*(A-mid)+bb*cc*(sa[C-1]-sa[A-1])+bb*(ac[B-1]-ac[C-1])+abc[r]-abc[B-1];
else if(B<=A&&A<=C) ans+=aa*bb*cc*(B-mid)+aa*cc*(sb[A-1]-sb[B-1])+cc*(ab[C-1]-ab[A-1])+abc[r]-abc[C-1];
else if(B<=C&&C<=A) ans+=aa*bb*cc*(B-mid)+aa*cc*(sb[C-1]-sb[B-1])+aa*(bc[A-1]-bc[C-1])+abc[r]-abc[A-1];
else if(C<=A&&A<=B) ans+=aa*bb*cc*(C-mid)+aa*bb*(sc[A-1]-sc[C-1])+bb*(ac[B-1]-ac[A-1])+abc[r]-abc[B-1];
else if(C<=B&&B<=A) ans+=aa*bb*cc*(C-mid)+aa*bb*(sc[B-1]-sc[C-1])+aa*(bc[A-1]-bc[B-1])+abc[r]-abc[A-1];
}
}
inline int read(){int ret=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}while(isdigit(ch)) ret=(ret<<1)+(ret<<3)+ch-'0',ch=getchar();return ret*f;}
int main(){
// freopen("d.in","r",stdin);freopen("d.out","w",stdout);
n=read();for(register int i=1;i<=n;i++) a[i]=read();for(register int i=1;i<=n;i++) b[i]=read();for(register int i=1;i<=n;i++) c[i]=read();
solve(1,n);for(register int i=1;i<=n;i++) a[i]=-a[i];solve(1,n);for(register int i=1;i<=n;i++) a[i]=-a[i];
for(register int i=1;i<=n;i++) swap(a[i],b[i]);for(register int i=1;i<=n;i++) a[i]=-a[i];solve(1,n);for(register int i=1;i<=n;i++) a[i]=-a[i];
for(register int i=1;i<=n;i++) swap(a[i],c[i]);for(register int i=1;i<=n;i++) a[i]=-a[i];solve(1,n);for(register int i=1;i<=n;i++) b[i]=-b[i];
solve(1,n);for(register int i=1;i<=n;i++) a[i]=-a[i];for(register int i=1;i<=n;i++) swap(a[i],c[i]);for(register int i=1;i<=n;i++) a[i]=-a[i];
solve(1,n);for(register int i=1;i<=n;i++) b[i]=-b[i];for(register int i=1;i<=n;i++) swap(b[i],c[i]);
for(register int i=1;i<=n;i++) b[i]=-b[i];solve(1,n);for(register int i=1;i<=n;i++) c[i]=-c[i];solve(1,n),cout<<ans<<'\n';return 0;
}

