义乌集训7.9 contest 2题解

2021.7.9 Contest 题解

​ 由于博主肝比较多，干脆把所有题都写了吧。这场比赛题目偏氵，AK理论上是没难度的，然而博主脑抽挂了几分QAQ。

T1:

Description:

​ 给定 \(n,m\) ，求有多少个正整数 \(x\)，使得 \(x^m \leq n\)。

Input:

​ 一行两个正整数 \(n,m\)。

Output:

​ 一行一个数表示正整数 \(x\) 的个数。

Sample1 Input:

5 2

Sample1 Output:

2

Hint:

对于 \(25\%\) 的数据，\(m=1\)。

对于 \(50\%\) 的数据，\(n\leq 10^6\)。

对于 \(100\%\) 的数据，\(1 \leq n,m \leq 10^{9}\)。

题目分析：

​ 简单题，\(m=1\) 时特判一下，其他情况直接枚举即可。

代码如下(马蜂很丑，不喜勿喷)——

#include<bits/stdc++.h>
#define N 100005
#define LL long long
using namespace std;
int n,m,ans=1;inline int read(){
	int ret=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}
	while(isdigit(ch)) ret=(ret<<1)+(ret<<3)+ch-'0',ch=getchar();return ret*f;
}
int main(){
	freopen("a.in","r",stdin);freopen("a.out","w",stdout);
	n=read(),m=read();if(m==1) cout<<n<<'\n',exit(0);if(m==2) cout<<(int)sqrt(n)<<'\n',exit(0);if(m>=30) puts("1"),exit(0);
	for(register int i=2;;i++){LL mul=1;for(register int j=1;mul<=n&&j<=m;j++) mul*=i;if(mul<=n) ans++;else break;}cout<<ans<<'\n';return 0;
}

T2:

Description:

​ 给定 \(n\)，你现在需要给整数 \(1\) 到 \(n\) 进行染色，使得对于所有的 \(1\leq i<j\leq n\)，若 \(i - j\) 为质数，则 \(i\) 和 \(j\) 不同色。

​ 求出颜色尽可能少的染色方案。如果有多种方案，输出任意一种即可。

Input:

​ 第一行一个整数 \(n\)。

Output:

​ 第一行一个整数 \(k\)，表示颜色数。

​ 第二行 \(n\) 个整数 \(col_i\)（\(1 \leq col_i \leq k\)），表示 \(i\) 的颜色。

Sample1 Input:

7

Sample1 Output:

4
1 2 2 3 3 4 1

Hint:

对于 \(30\%\)的数据，\(n \leq 10\)；

对于 \(60\%\) 的数据，\(n \leq 20\)；

对于 \(100\%\) 的数据，\(n \leq 10^4\)。

题目分析：

​ 构造题，如果感觉不好可以随便写个dfs打个表就能发现 \(n \geq 7\) 时，\(k=4\)，构造方案形如 \(1,2,3,4,1,2,3,4,1,2,3,4……\)

​ 证明显然。对于颜色相同的两个数 \(x,y\)，满足\(|x-y|= 4z (z ∈ N)\) ，故\(|x-y|\)一定不是质数，方案合法。

​ 对于 \(n \leq 6\) 直接跑dfs或者直接手玩即可。

代码如下(马蜂很丑，不喜勿喷)——

#include<bits/stdc++.h>
#define N 100005
#define LL long long
using namespace std;
int n,tot,pri[N],a[N];bool ok[N],vis[N];inline int read(){
	int ret=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}
	while(isdigit(ch)) ret=(ret<<1)+(ret<<3)+ch-'0',ch=getchar();return ret*f;
}
int main(){
	freopen("b.in","r",stdin);freopen("b.out","w",stdout);
	n=read();if(!n) return puts("0"),0;if(n<7){
		a[1]=1,ok[1]=1;for(register int i=2;i<=n;i++)
		{if(!ok[i]) pri[++tot]=i;for(register int j=1;j<=tot&&i*pri[j]<=n;j++){ok[i*pri[j]]=1;if(i%pri[j]==0) break;}}
		tot=1;for(register int i=2;i<=n;i++){
			for(register int j=1;j<=tot;j++) vis[j]=1;bool flg=0;
			for(register int j=1;j<i;j++) if(!ok[i-j]) vis[a[j]]=0;
			for(register int j=1;j<=tot;j++) if(vis[j]){a[i]=j,flg=1;break;}if(!flg) a[i]=++tot;
		}
		cout<<tot<<'\n';for(register int i=1;i<=n;i++) cout<<a[i]<<' ';return 0;
	}
	cout<<4<<'\n';for(register int i=1,j=1;i<=n;i++,j=j%4+1) cout<<j<<' ';return 0;
}

T3:

Description:

​ 小QwQ 在批改作业的时候发现大家的提交的文件名都很不规范，这让他很头疼。作为一个强迫症患者，他决定手动规范大家的文件名。但是有些人的文件名特别长，他想要知道最少需要修改多少次才能够使得字符串 \(A\) 变成字符串 \(B\)。当然对于修改代价超过 \(K\) 的文件名我们会选择放弃。

​ 定义一次修改代价：

1. 在第 \(i\) 个位置插入一个字符
   \(...S_{i-1}S_{i}S_{i+1}...\Rightarrow S_{i-1}KS_{i}S_{i+1}\)

2. 删除第 \(i\) 个位置的字符
   \(...S_{i-1}S_{i}S_{i+1}...\Rightarrow S_{i-1}S_{i+1}...\)

Input:

​ 输入共包含 \(3\) 行。

​ 第 \(1\) 行包含三个整数 \(n,m,K\)，分别表示原始串 \(A\) 的长度,目标串 \(B\) 的长度和限制的最大修改次数。

​ 接下来 \(2\) 行，分别输入原始字符串 \(A\) 和目标字符串 \(B\)。

Output:

​ 输出共包含 \(1\) 行，如果最小修改次数小于等于 \(K\)，则输出最少修改次数，不然输出 \(-1\)。

Sample1 Input:

3 4 2
bee
beef

Sample1 Output:

1

Hint:

对于其中 \(25\%\) 的数据，\(n,m\le10\)。

对于其中 \(50\%\) 的数据，\(n,m\le1000\)。

对于另外 \(25\%\) 的数据，\(K\le10\)。

对于 \(100\%\) 的数据，满足 \(0\le n,m\le500000,0\le K\le100\)。字符串中只包含小写字母。

题目分析：

​ 首先我们发现加字母的操作可以转化为删除操作。

​ 考虑DP，最朴素的想法就是考虑 \(A\) 的第 \(i\) 位与 \(B\) 的第 \(j\) 位匹配所需的最少修改次数。然而这样的复杂度是 \(O(nm)\) 的。

​ 经过思考可以发现，由于 \(K\) 的范围很小，于是 \(A\) 的第 \(i\) 位只能与 B 的第 \([i-K+1,i+K-1]\)匹配，于是我们就能把复杂度优化到 \(O(nK)\) ，可以通过此题。

​ 具体实现的时候可以采用前缀和优化。(然而还有其他更简单的实现方法)

代码如下(马蜂很丑，不喜勿喷)——

#include<bits/stdc++.h>
#define N 500005
#define M 105
#define LL long long
#define inf 214748364
using namespace std;
int n,m,K,g[N+M*2],f[N+M*2];char A[N],B[N];inline int read(){
	int ret=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}
	while(isdigit(ch)) ret=(ret<<1)+(ret<<3)+ch-'0',ch=getchar();return ret*f;
}
int main(){
	n=read(),m=read(),K=read();if(abs(n-m)>K) puts("-1"),exit(0);scanf("%s%s",A+1,B+1);
	if(n>m){for(register int i=1;i<=m;i++) swap(A[i],B[i]);for(register int i=m+1;i<=n;i++) B[i]=A[i];swap(n,m);}
	for(register int i=0;i<K;i++) g[i]=inf;for(register int i=K;i<=n+2*K;i++) g[i]=-2-K;A[++n]='@',B[++m]='@';for(register int i=1;i<=n;i++){
		int up=min(m+K-i,K<<1);for(register int j=max(K+1-i,0);j<=up;j++){
			if(i==n&&i+j-K==m){int x;if(i+j-2>=0) x=min(g[i+j-1],g[i+j-2]);else x=g[i+j-1];x+=2*i+j;if(x<=K) cout<<x<<'\n';else puts("-1");return 0;}
			if(A[i]==B[i+j-K]) if(i+j-2>=0) f[i+j]=min(g[i+j],min(g[i+j-1],g[i+j-2])-2);else f[i+j]=min(g[i+j],g[i+j-1]-2);
			else if(i+j-2>=0) f[i+j]=min(g[i+j],min(g[i+j-2],g[i+j-1]));else f[i+j]=min(g[i+j],g[i+j-1]);
		}
		for(register int j=max(K+1-i,0);j<=up;j++) g[i+j]=min(g[i+j],f[i+j]),g[i+j]=min(g[i+j],g[i+j-1]);
	}
	puts("-1");return 0;
}
/*
4 4 2
abcd
adbd
*/

T4:

Description:

​ 你有一棵 \(n\) 节点的树 \(T\)，回答 \(m\) 个询问，每次询问给你两个整数 \(l,r\)，问存在多少个整数 \(k\) 使得从树上编号为 \(l\) 的点沿着 \(l\to r\) 的简单路径走 \(k\) 步恰好到达 \(k\)。

Input:

​ 第一行，两个整数 \(n,m\) 表示节点数和询问数。

​ 之后 \(n-1\) 行，每行两个整数 \(u,v\) 表示一条边。

​ 之后 \(m\) 行，每行两个整数 \(l,r\) 表示 一个询问，题意同题目描述。

Output:

​ \(m\) 行，对于每个询问单独输出一行表示你的答案。

Sample1 Input:

9 3
5 4
4 3
3 7
4 1
1 6
1 8
1 9
5 2
6 7
2 3
3 2

Sample1 Output:

2
1
0

Hint:

sample explaination:

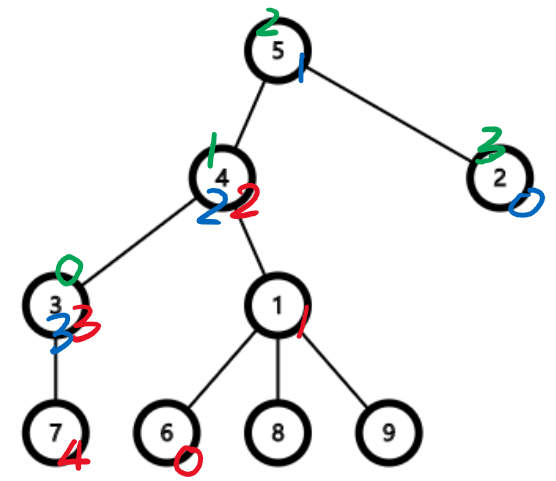
如图，红色表示第一次询问中 \(k=0,1,\ldots,4\) 的情况，蓝色表示第二次询问，绿色是第三次询问。

其中，在第一次询问中：

• 走 \(0\) 步到达 \(6\)，不符题意。

• 走 \(1\) 步到达 \(1\)，满足题意。

• 走 \(2\) 步到达 \(4\)，不符题意。

• 走 \(3\) 步到达 \(3\)，满足题意。

• 走 \(4\) 步到达 \(7\)，不符题意。

data range:

测试点编号	\(n\le\)	\(m\le\)	特殊性质
\(1\sim 3\)	\(10\)	\(10\)	ACD
\(4\sim 6\)	\(100\)	\(100\)	ACD
\(7\sim 10\)	\(500\)	\(500\)	ABCD
\(11\sim 13\)	\(10^4\)	\(10^4\)	ABD
\(14\sim 16\)	\(10^5\)	\(10^5\)	ABD
\(17\sim 20\)	\(3\times 10^5\)	\(3\times 10^5\)	CDDD

其中特殊性质一栏中，每个字符分别表示该测试点满足的性质。例如 \(4\sim 6\) 行中的"ACD"表示#4满足A，#5满足C，#6 满足 D。

• A： 一条链
• B： 深度不超过 \(50\)
• C： 将 \(1\) 作为根时会形成一棵二叉树
• D： 无性质

题目分析：

​ 树剖套路题。找到 \(LCA\), 把一条路径拆成两条链，每条链分别推个柿子。对于\(x->LCA->y\) :

1. \(x->LCA\) ：\(dep[i]+i=dep[x]\)

2. \(LCA->y\) ：\(dep[y]-(dep[x]+dep[y]-2*dep[LCA]-i)=dep[i] -> dep[i]-i=2*dep[LCA]-dep[x]\)

​ 最后用vector存一下然后直接查询即可，常数很小。

代码如下(马蜂很丑，不喜勿喷)——

#include<bits/stdc++.h>
#define N 300005
#define s_id vector<int>::iterator
using namespace std;
int n,m,tot,s1,s2,f[N],w[N],s[N],top[N],dfn[N],rk[N],fir[N],nxt[N<<1],son[N<<1],dep[N];
vector<int> g1,g2,F1[N],F2[N];inline void add(int x,int y){son[++tot]=y,nxt[tot]=fir[x],fir[x]=tot;} inline void dfs(int x){
	dep[x]=dep[f[x]]+1,s[x]=1,g1.push_back(dep[x]+x),g2.push_back(dep[x]-x);
	for(register int i=fir[x];i;i=nxt[i]) if(son[i]!=f[x]) f[son[i]]=x,dfs(son[i]),s[x]+=s[son[i]],(s[w[x]]<=s[son[i]])&&(w[x]=son[i]);
}
inline void dfs2(int x,int tp){top[x]=tp,dfn[x]=++tot,rk[tot]=x;if(w[x]) dfs2(w[x],tp);for(register int i=fir[x];i;i=nxt[i]) if(son[i]!=f[x]&&son[i]!=w[x]) dfs2(son[i],son[i]);}
inline int get1(int x){return lower_bound(g1.begin(),g1.end(),x)-g1.begin();}
inline int get2(int x){return lower_bound(g2.begin(),g2.end(),x)-g2.begin();}
inline int LCA(int x,int y){while(top[x]^top[y]) if(dep[top[x]]>dep[top[y]]) x=f[top[x]];else y=f[top[y]];if(dep[x]<dep[y]) return x;return y;}
inline int Q1(int l,int r,int x){return upper_bound(F1[x].begin(),F1[x].end(),r)-lower_bound(F1[x].begin(),F1[x].end(),l);}
inline int Q2(int l,int r,int x){return upper_bound(F2[x].begin(),F2[x].end(),r)-lower_bound(F2[x].begin(),F2[x].end(),l);}
inline int solve(int x,int y){
	int lca=LCA(x,y),res=0,xx=x,x1=get1(dep[xx]),x2=get2(2*dep[lca]-dep[xx]);
	if(x1<s1&&g1[x1]==dep[xx]) ;else x1=-1;if(x2<s2&&g2[x2]==2*dep[lca]-dep[xx]) ;else x2=-1;while(top[x]^top[y]){
		if(dep[top[x]]>dep[top[y]]) (x1!=-1)&&(res+=Q1(dfn[top[x]],dfn[x],x1),0),x=f[top[x]];
		else (x2!=-1)&&(res+=Q2(dfn[top[y]],dfn[y],x2),0),y=f[top[y]];
	}
	if(dep[x]>=dep[y]) (x1!=-1)&&(res+=Q1(dfn[y],dfn[x],x1),0);else (x2!=-1)&&(res+=Q2(dfn[x],dfn[y],x2),0);return res;
}
inline int read(){
	int ret=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}
	while(isdigit(ch)) ret=(ret<<1)+(ret<<3)+ch-'0',ch=getchar();return ret*f;
}
int main(){
//	freopen("d.in","r",stdin);freopen("d.out","w",stdout);
	n=read(),m=read();for(register int i=1,x,y;i<n;i++) x=read(),y=read(),add(x,y),add(y,x);tot=0,dfs(1),dfs2(1,1),tot=0;
	sort(g1.begin(),g1.end()),g1.erase(unique(g1.begin(),g1.end()),g1.end()),s1=g1.size(),sort(g2.begin(),g2.end()),g2.erase(unique(g2.begin(),g2.end()),g2.end()),s2=g2.size();
	for(register int i=1;i<=n;i++) F1[get1(rk[i]+dep[rk[i]])].push_back(i),F2[get2(dep[rk[i]]-rk[i])].push_back(i);
	while(m--){int x=read(),y=read();cout<<solve(x,y)<<'\n';}return 0;
}