无损卡尔曼滤波UKF(2)-简介
1 新来的无损卡尔曼滤波器有什么不一样呢?
对于非线性模型,比如我们前面使用的CVTR
经过这样的模型预测出来的状态就不会是正态分布的了
那么我们就没法用传统的卡尔曼滤波器
当然,可以选择使用扩展卡尔曼滤波,非线性函数,泰勒展开线性化呗
你愿意这么做,也可以,但是你就得算雅克比矩阵不是么
新来的无损卡尔曼滤波呢,就让你不用再算Jacobi矩阵了哦
他就是 处理非线性函数时,他就是进行了无损转换
怎么说呢?
就是把非线性过程模型的结果,就是这个谁也不知道什么分布的结果
他给转换成了一个正态分布的结果!!
还能表示一样的状态。
那接下来呢??
求一个分布的均值和协方差,接着迭代呗
所以其他部分,和我们的卡尔曼滤波没啥区别
重点就是,把非线性函数处理来的结果,转换了
那他到底是怎么转换的呢??

2 无损卡尔曼滤波器到底是怎么无损转换的呢??
好的,关键词来了 ----Sigma点----
你好问了,这是什么玩意?
大家都知道,使用非线性函数对整个状态分布,进行转换,很有难度
但是啊,你把分布A的某个点,由非线性模型转换到分布B的某个点,就很简单。带进函数求个值就完了
分布A就是我们后验嘛,就是上一轮迭代出来的。
分布B呢,先验呗,我们要预测的状态,但是现在我们还不知道他是个啥
Sigma点是什么呢?
他们分布在状态均值的周围,和每一个状态大小的标准差的和有一定关系
他们就可以代表整个分布。
所以得到当前分布的Sigma点之后,带进非线性函数,算出一组新的Sigma点。
那么,得到的这组新的Sigma点不就是代表了分布B么
所以求出这组Sigma的均值和方差就可以下一步迭代了
好的,总结一下流程
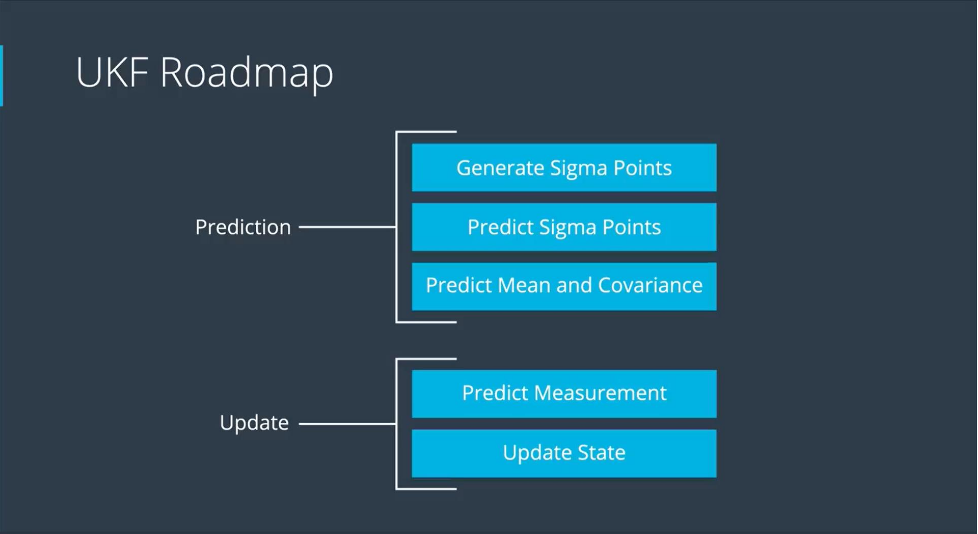
- 选择sigma点
- 预测sigma点
- 根据得到的sigma点,计算均值和方差
本文来自博客园,作者:longlongban,转载请注明原文链接:https://www.cnblogs.com/jiangxinyu1/p/12462491.html
简单学习分享,如有错误欢迎指正


