无损卡尔曼滤波UKF(1)-预测--从CTRV过程模型开始

无损卡尔曼滤波UKF（1）-从CTRV过程模型开始

无损卡尔曼滤波

1. 处理非线性过程模型和非线性测量模型的替代方法
2. 不会对非线性函数进行线性化处理
3. 用所谓的sigma点来近似概率分布
4. 省去计算雅阁比矩阵的部分

过程模型

1 CV模型的缺陷：

In the extended kalman filter lesson, we used a constant velocity model (CV).
A constant velocity model is one of the most basic motion models used with object tracking.

1. 实际上简化了车辆的运动方式，大多数道路是有转弯的。
2. 速度为常量，拐弯的你就没法整了。
   

2 其他模型

1. constant turn rate and velocity magnitude model (CTRV)
2. constant turn rate and acceleration (CTRA)
3. constant steering angle and velocity (CSAV)
4. constant curvature and acceleration (CCA)

3 CTRV 模型确定性部分推导

1. 固定的转弯速率
2. 恒定的速度大小

3.1 状态向量

\(x = [px,py,v,\phi,\dot{\phi}]^T\)

1. 位置px py
2. 速度大小 v
3. 偏航角 φ
4. 角速度 φ.

3.2 过程模型推导

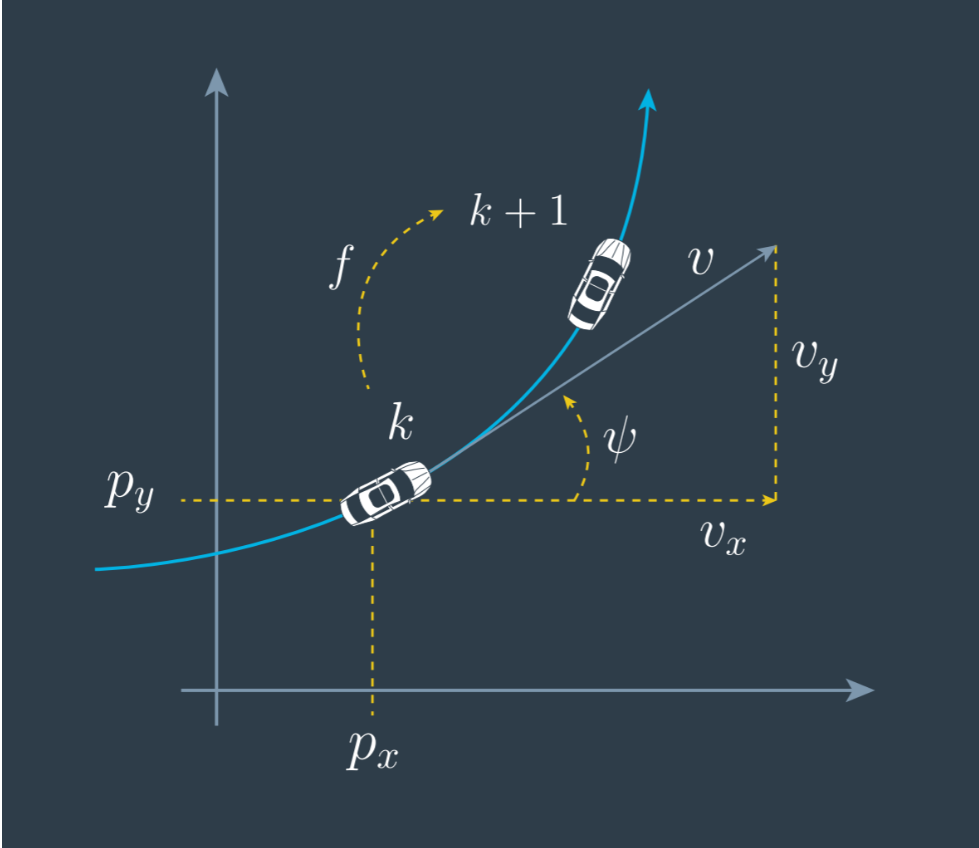
\(x_{k+1} = f(x_k,v_k);\)

噪声向量vk就是需要我们建模时推导的函数

先讨论状态x的变更速率

\(x = [px,py,v,\phi,\dot{\phi}]^T\)

\(\dot{x} = [\dot{p_x},\dot{p_y},\dot{v},\dot{\phi},\ddot{\phi}]^T\)

其中g(x)的各变量

\(\dot{p_x} = v_x = cos(\phi) \cdot v\)

\(\dot{p_y} = v_y = sin(\phi) \cdot v\)

\(\dot{v} = 0\)

\(\dot{\phi} = \dot{\phi}\)

\(\ddot{\phi} = 0\)

推出差分方程

\(\dot{x} = g(x) = [cos(\phi)\cdot v, sin(\phi)\cdot v , 0 ,\dot{\phi} ,0 ]^T\)

求时间差

\(\Delta t = t_{k+1} - t_k\)

在时间差内求积分 就可以求得时间差内各项的变化，也就是确定性部分的预测方程
\(x_{k+1} = x_k + \int^{t_{k+1}}_{t_k}{g(x)}{\rm d}t\)

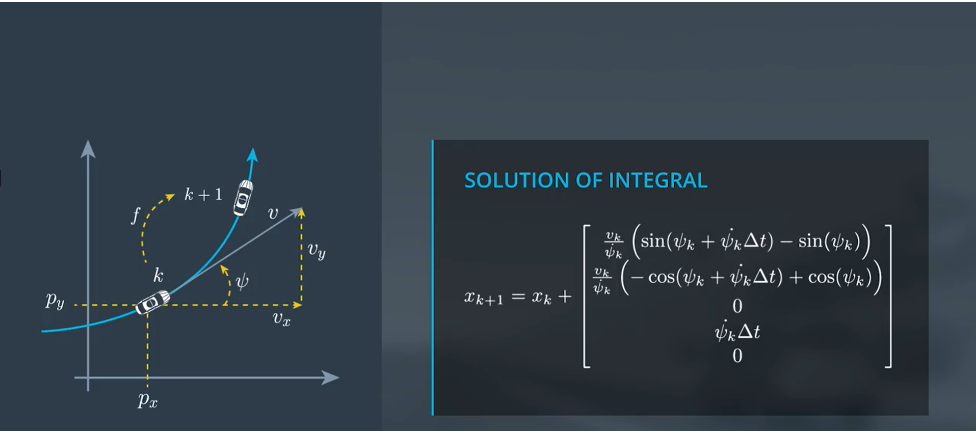
特殊情况：角速度为0的时候

\(p_{x_{k+1}} = p_{x_k} + cos(\phi)\cdot v_k \cdot \Delta t\)

\(p_{y_{k+1}} = p_{y_k} + sin(\phi)\cdot v_k \cdot \Delta t\)

4 CTRV 模型噪声向量推导

过程模型噪声分为两个部分

我们的CTRV模型，假设了车的纵向速度和角速度为恒定值，忽略了速度的变化。

因此要把加速度项的影响放到误差项里面。

1. 纵向加速度噪声va，表示在纵向速度上的不确定性，因此可以定义为，正态分布的白噪声，以0为均值

\(\nu_{a,k} - N (0,\sigma^2_a )\)

2. 角加速度噪声vφ..，表示偏航角速度上的不确定性，因此可以定义为，正态分布的白噪声，以0为均值

\(\nu_{\ddot{\phi},k} - N (0,\sigma^2_{\ddot{\phi}} )\)

因此，过程噪声向量为：

\(\nu_k = [ \nu_{a,k} , \nu_{\ddot{\phi},k} ]^T\)

考虑噪声向量对整个过程的影响：

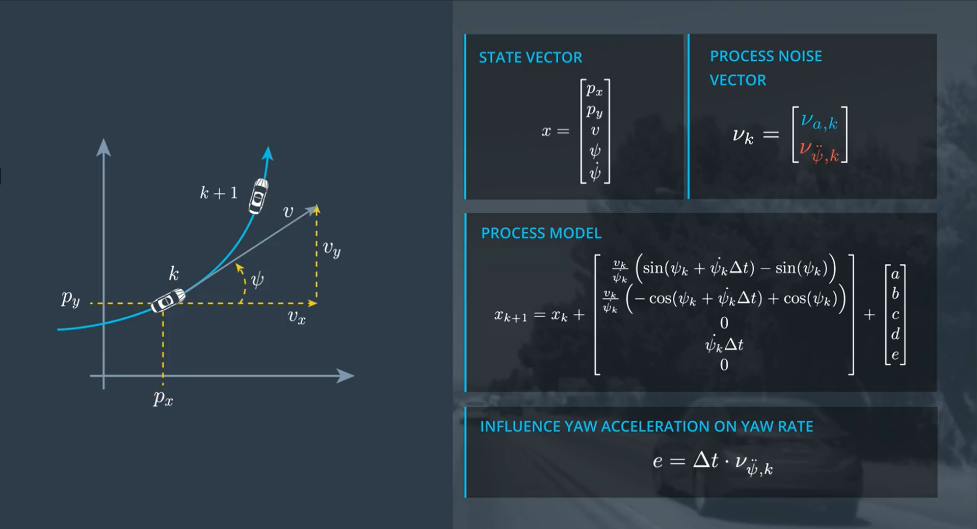
假设误差项-偏航角角加速度和纵向加速度是常量，那么在时间差内产生的误差a,b,c,d,e ，就可以定义为

\(a = (1/2) \cdot \nu_{a,k} \cdot cos(\phi_k) \cdot (\Delta t )^2\)

\(b = (1/2) \cdot \nu_{a,k} \cdot sin(\phi_k) \cdot (\Delta t )^2\)

\(c = \Delta t \cdot \nu_{a,k}\)

\(d = (1/2)\cdot \nu_{\ddot{\phi},k} \cdot (\Delta t )^2\)

\(e = \Delta t \cdot \nu_{\ddot{\phi},k}\)

注意上式中的

\(\nu_{a,k}\)- 和 -\(\nu_{\ddot{\phi},k}\)

分别代表误差项中的纵向加速度项和角加速度项，并不是速度。

到此，CTRV模型的各项我们已经推导结束。