Deep Knowledge Tracing (深度知识追踪)
Addressing Two Problems in Deep Knowledge Tracing via Prediction-Consistent Regularization
How Deep is Knowledge Tracing?
tensorflow代码实现:https://github.com/jiangxinyang227/dkt
1、概述
知识追踪是对学生的知识基于时间建模,以便我们能精确预测学生对于知识点的掌握程度,以及学生在下一次的表现。而且精确的知识追踪能让我们抓住学生当前的需求,并进行精准推题。然而人类的学习过程中受到人类自身知识和大脑两者的复杂的影响的,也导致知识追踪是非常困难的。
早期的知识追踪模型都是依赖于一阶马尔科夫模型,例如贝叶斯知识追踪(Bayesian Knowledge Tracing)。在本文中引入灵活的循环神经网络来处理知识追踪任务。
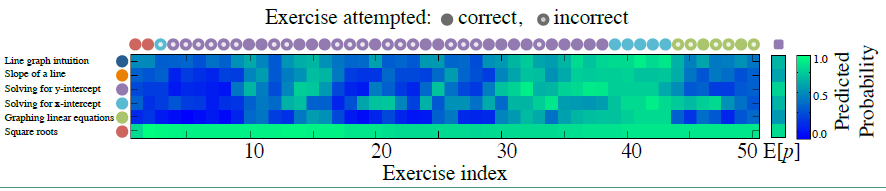
知识追踪任务可以概括为:给定一个学生在某一特定学习任务上的表现的观测序列 ${x_0, x_1, ......, x_t}$ ,预测他们在下一次的表现 $x_{t+1}$ 。下图描述了一个学生在学习八年级数学课室的知识追踪可视化展示。这个学生一开始答对了两个关于平方根的问题,然后答错了一道关于X-轴截距的题,接下来做了一系列关于X-轴截距、Y-轴截距和线性方程作图的题目(在这里平方根、X-轴截距、Y-轴截距等都可以看作是一个知识点)。在学生做完每一道练习时我们都可以预测他在下一道题目上的表现,题目可以是来源于不同知识点的题目。在这个图中我们只预测了和当前练习题相关的知识点的掌握情况。
2、模型
贝叶斯知识追踪(BKT)是最流行的知识追踪模型。在BKT模型中提出了一个关于学生知识状态的隐变量,学生的知识状态由一个二元组表示 {掌握该知识点,没掌握该知识点}。整个模型结构实际上是一个HMM模型,根据状态转移矩阵来预测下一个状态,根据当前的状态来预测学生的答题结果。而且在BKT模型中认为知识一旦掌握就不会被遗忘。并且在当前的工作中还引入了学生未掌握知识的情况下猜对题目的概率和学生掌握知识的情况下答错题目的概率,学生的先验知识和问题的难度来扩展模型。然而不管有没有这些扩展,BKT模型依然存在几个问题:
1)学生的知识状态用二元组表示并不是很实际。
2)隐藏状态和练习做题之间的映射模糊,很难充分预测每个练习的某个概念
3)观测状态的二元组表示会限制题目的类型
循环神经网络是一种时间序列的模型,信息是基于早期的信息和当前输入的信息进行递归传播的。相对于HMM,RNN具有高维,连续的隐藏状态表示。RNN最大的优势在于能利用更多的早期的信息,尤其是RNN的变种LSTM网络结构。RNN在很多时间序列问题上都取得了非常好的结果,因此将RNN应用到知识追踪上也许会有更好的结果。
在这里我们可以用传统的RNN或者是LSTM模型。在将数据输入到模型之前我们要将输入的数据转换成向量表示(输入的数据就是我们观测到的学生做题的结果)。输入值的向量表示有两种方式:
1)one-hot表示。假设在我们的模型中的数据中涉及到M个知识点,所有的题目都属于这M个知识点,每道题的结果有两种 {对,错},对于某一道属于第 $i$ 个知识点,做对时向量表示为第 $M + i$ 个位置为1,其余位置为0;做错时第 $i$ 个位置为1,其余位置为0,向量总长度为2M(注意整个模型只关注题目所属知识点,和做题的结果)。one-hot 的表示比较方便,但是一旦知识点的数量非常大之后,向量就会变得高维、稀疏。
2)通过压缩感知算法将高维稀疏的输入数据进行压缩到低维空间( $\log {2M}$ )中。
输出结果 $y_t$ 是一个长度为 M 的向量,向量中的每一个值描述的是对应的知识点的掌握概率(或者说对应的知识点下的题目答对的概率)。因此,整个序列就是根据前 $i-1$ 个时间步的信息来预测 第 $i$ 步对各知识点的掌握情况。
模型的损失函数为:

在上面$n$是指学生的数量,$T_i$指的是第 $i$个学生的序列长度,$l(.)$是交叉熵损失。
3、DKT的优势
很多研究表明DKT模型在各种开源数据集上的表现基本都由于传统的BKT模型。相关论文表明DKT的优势主要在于:
1)近因效应
在当前时间学生的做题结果是会受到近期学生在这些知识点上的表现的影响的,在BKT模型中假定学生一旦掌握某一知识点,对该知识点就不会遗忘,学生在以后做到属于该知识点的题目时往往就会表现很好。而实际上并不是这样的,时间久了,学生也可能会遗忘之前掌握的知识点。而DKT模型能很好的捕捉学生最近的表现来预测学生的做题结果,能更多的利用学生最近的表现。
2)上下文试验序列
学生在做题的过程中,可能是多个知识点的题较叉练习,例如学生在知识点A,B 上的做题顺序是 $ A_1 - B_1 - A_2 - B_2 - A_3 - B_3 $ 。BKT只能在单个知识点建模,无法将学生这样的做题顺序给表述出来。而DKT能针对多个知识点建模,能很好的表述这样的做题顺序。
3)知识点内在相关性
实际情况中,知识点与知识点之间是具有相关性的,如最上面的图所示,X-截距、Y-截距和线性方程等之间都是具有很强的相关性的。BKT由于只能对单个知识点建模,因此无法将这些相关性表示出来。而DKT可以对多个知识点建模,且神经网络可以根据学生的做题结果获得知识点之间的关系。
4)个体之间的能力差异
DKT 能根据该学生在各个知识点上的表现情况来获得学生的平均能力(该能力能一定程度代表学生的学习能力),而BKT 由于只能在单个知识点上建模,因此无法获得学生在各知识点上的平均水平。
4、DKT的不足
DKT当前在学生知识点追踪上获得了良好的表现,然而其依然存在一些不足,主要有两个方面:
1)模型没法重构当前的输入结果
2)在时间序上学生对知识点的掌握度不是连续一致,而是波动的
具体的如下图所示

1)例如当前输入是 $(s_{32}, 0)$ ,然而在之后的预测结果却是做题正确。反之亦然,作者认为出现这种情况是因为定义的损失函数没有考虑时间 $t$ 的输入值,只考虑了时间 $t$ 的输出结果和时间 $t+1$ 的输入值。因此作者引入一个正则项来消除这种现象,正则项的表达式如下:
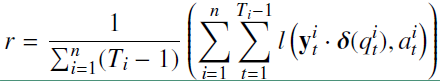
2)在上图中中间段,不断的练习 $s_{32}, s_{33}$ ,发现学生的能力在不断的波动,而没有一致性。为了解决这个问题,作者引入了两个正则项( $L_1$ 和 $L_2$ 正则,相当于弹性网),正则项的表达式如下:

在上面$n$是指学生的数量,$T_i$指的是第 $i$个学生的序列长度。
最后损失函数如下:
![]()



