自然语言处理之LDA主题模型
1、LDA概述
在机器学习领域,LDA是两个常用模型的简称:线性判别分析(Linear Discriminant Analysis)和 隐含狄利克雷分布(Latent Dirichlet Allocation)。本文的LDA仅指代Latent Dirichlet Allocation. LDA 在主题模型中占有非常重要的地位,常用来文本分类。
LDA是基于贝叶斯模型的,涉及到贝叶斯模型离不开“先验分布”,“数据(似然)”和"后验分布"三块。在贝叶斯学派中有:
先验分布 + 数据(似然)= 后验分布
这点其实很好理解,因为这符合我们人的思维方式,比如你对好人和坏人的认知,先验分布为:100个好人和100个的坏人,即你认为好人坏人各占一半,现在你被2个好人(数据)帮助了和1个坏人骗了,于是你得到了新的后验分布为:102个好人和101个的坏人。现在你的后验分布里面认为好人比坏人多了。这个后验分布接着又变成你的新的先验分布,当你被1个好人(数据)帮助了和3个坏人(数据)骗了后,你又更新了你的后验分布为:103个好人和104个的坏人。依次继续更新下去。
2、预备知识
2.1 词袋模型
LDA 采用词袋模型。所谓词袋模型,是将一篇文档,我们仅考虑一个词汇是否出现,而不考虑其出现的顺序。在词袋模型中,“我喜欢你”和“你喜欢我”是等价的。与词袋模型相反的一个模型是n-gram,n-gram考虑了词汇出现的先后顺序。
2.2 二项分布
伯努利分布是只有两种可能结果的单次随机试验,二项分布(Binomial distribution)是n重伯努利试验成功次数的离散概率分布,即为X ~ B(n, p). 概率密度公式为:
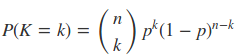
2.3 多项分布
多项式分布(Multinomial Distribution)是二项式分布的推广。二项式做n次伯努利实验,规定了每次试验的结果只有两个,如果现在还是做n次试验,只不过每次试验的结果可以有多k个,且k个结果发生的概率互斥且和为1,则发生其中一个结果X次的概率就是多项式分布。概率密度函数为:
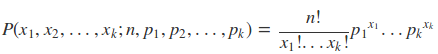
2.4 Beta分布
beta分布可以看作一个概率的概率分布,当你不知道一个东西的具体概率是多少时,它可以给出了所有概率出现的可能性大小。
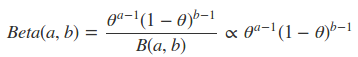
假设此时的二项分布为
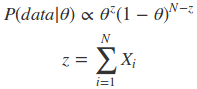
贝叶斯估计为
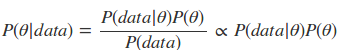
现在我们有了二项分布的似然函数和beta分布,现在我们将beta分布代进贝叶斯估计中的P(θ)中,将二项分布的似然函数代入P(data|θ)中,可以得到:
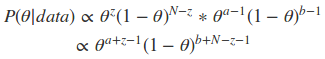
我们设a′=a+z,b′=b+N−z,最后我们发现这个贝叶斯估计服从Beta(a’,b’)分布的,我们只要用B函数将它标准化就得到我们的后验概率:
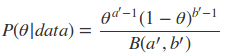
如上面这种形式,先验分布和后验分布的形式是同一种分布,像这样的分布我们称为共轭分布,而和二项分布共轭的分布就是Beta分布。
而共轭的意思是,以Beta分布和二项式分布为例,数据符合二项分布的时候,参数的先验分布和后验分布都能保持Beta分布的形式,这种形式不变的好处是,我们能够在先验分布中赋予参数很明确的物理意义,这个物理意义可以延续到后续分布中进行解释,同时从先验变换到后验过程中从数据中补充的知识也容易有物理解释。
2.5 狄利克雷分布
狄利克雷分布是多项分布的共轭分布,也是Beta分布的一般形式。概率密度函数如下:
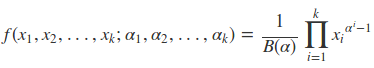
其中
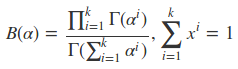
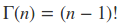
Beta分布的期望求解:
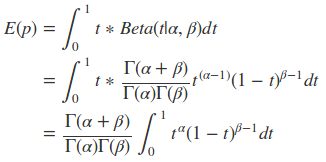
对于上面的分布有
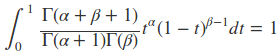
因此可以得到
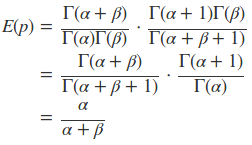
这说明,对于对于Beta分布的随机变量,其均值可以用α/α+β来估计。而对于狄利克雷分布同样有
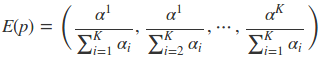
3、LDA主题模型
LDA的特点:
1)它是一种无监督的贝叶斯模型。
2)是一种主题模型,它可以将文档集中的每篇文档按照概率分布的形式给出。
3)是一种无监督学习,在训练时不需要手工标注的训练集,需要的是文档集和指定主题的个数。
4)是一种典型的词袋模型,它认为一篇文档是由一组词组成的集合,词与词之间没有顺序和先后关系。
3.1 LDA的简单理解
同一主题下,某个词出现的概率,以及同一文档下,某个主题出现的概率,两个概率的乘积,可以得到某篇文档出现某个词的概率,我们在训练的时候,只需要调整这两个分布。具体如下图所示
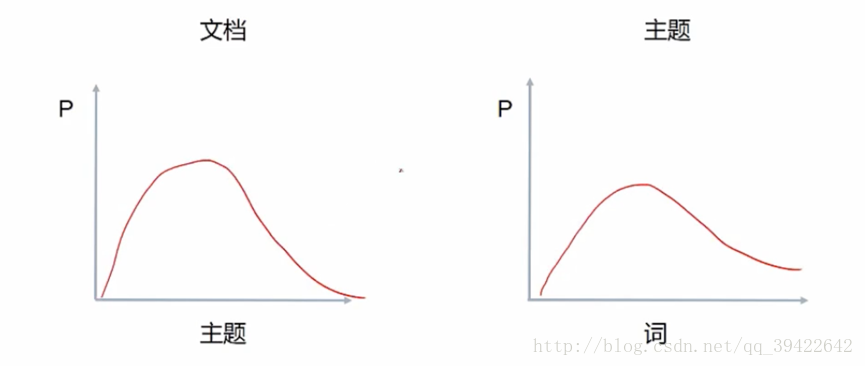
LDA生成文档的流程如下:
1) 按照先验概率p(di)选择一篇文档di
2)从Dirichlet分布α中取样生成文档di的主题分布θi,主题分布θi由超参数为α的Dirichlet分布生成
3)从主题的多项式分布θi中取样生成文档di第 j 个词的主题zi,j
4)从Dirichlet分布β中取样生成主题zi,j对应的词语分布ϕzi,j,词语分布ϕzi,j由参数为β的Dirichlet分布生成
5)从词语的多项式分布ϕzi,j中采样最终生成词语ωi,j
3.2 LDA的数学理解
在LDA中,主题分布和词分布是不确定的,LDA的作者们采用的是贝叶斯派的思想,认为它们应该服从一个分布,主题分布和词分布都是多项式分布,因为多项式分布和狄利克雷分布是共轭结构,在LDA中主题分布和词分布使用了Dirichlet分布作为它们的共轭先验分布。
LDA模型如下图所示
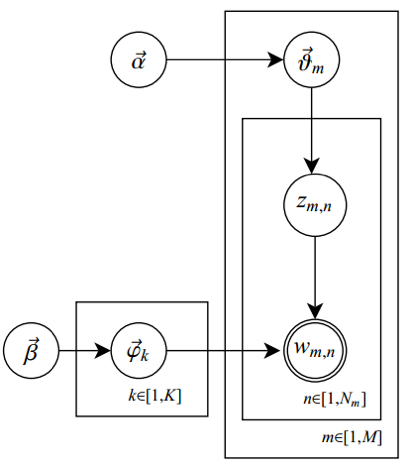
我们来看看LDA模型的物理过程分解,主要分为两个狄利克雷-多项式共轭分布过程:第一是文档主题的先验分布(狄利克雷分布)和每一个主题的多项式分布;第二是主题中词的先验分布(狄利克雷分布)和每一个词的多项式分布。
过程一:
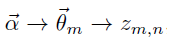
这个过程表示在生成第m篇文档时,先生成对应的主题分布(主题分布是变化的,要根据狄利克雷分布中的超参数α来生成):
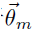
然后根据这个主题分布获得生成文档中第n个词的主题:
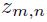
过程二:
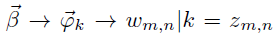
这个过程先获得第k个主题的词分布(该词分布是变化的,要根据狄利克雷分布中的超参数β来生成):
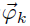
其中

然后根据词的多项式分布来生成词
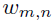
由第一个过程可知
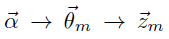
是表示生产第m篇文档中的所有词对应的主题,显然,
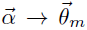
上面的式子对应狄利克雷分布
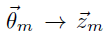
上面的式子对应多项式分布,所以整体上是一个狄利克雷-多项式的共轭结构
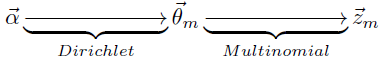
对于第m篇文档的主题生成概率可以表示为

由于语料中M篇文档的主题的生成过程相互独立,因此整个语料中的主题的生成概率
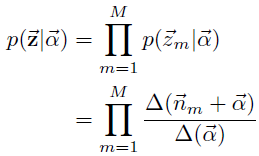
在这里我们得到了第一个共轭分布的表达式
由第二个过程可知
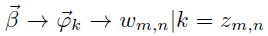
语料中任何两个由主题k生成的词都是可以交换的,即使他们不在同一个文档中(因为这两个过程是相互独立的),所以此处不考虑文档的概念,则上式可以表述为:
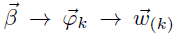
因此可以看出
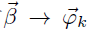
是对应于狄利克雷分布,而
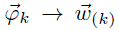
是对应于对象时分布的,所以整体也是一个狄利克雷-多项式的共轭分布:
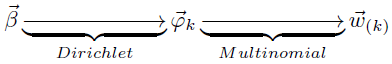
与第一个过程同理,可以得到共轭分布表达式:
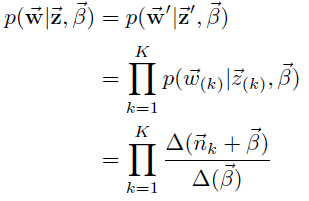
结合第一个过程的共轭分布表达式,可以得到语料中词和主题的联合生成概率
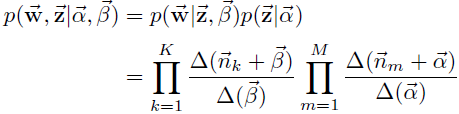
具体的LDA模型求解采用Gibbs采样算法,现成的库可以用gensim,gensim.models.ldamodel.LdaModel()类可以生成LDA模型。
4、总结
LDA可以看作是由四个概率分布组成的(两个狄利克雷分布和多项式分布),也可以看作是两个狄利克雷-多项式共轭分布组成的。
所以这四个概率分布如下:
第一个狄利克雷分布生成主题分布模型,且该主题分布模型服从多项式分布(相当于主题分布有多种)
第一个多项式分布用来生成某一个主题(获得某一个确定的主题分布之后就可以获得确定的主题)
第二个狄利克雷分布生成词分布模型,且该词服从多项式分布(相当于词分布有多种)
第二个多项式分布用来生成某一个词(获得某一个确定的词分布之后就可以获得确定的词,该确定的词分布是和确定的主题有关的)
参考文献:



