自然语言处理之信息论基础

熵

　　如果X是一个离散型随机变量, 取值空间为R, 那么X的熵H(X)定义为式

　　

联合熵和条件熵

　　如果X,Y是一对离散型随机变量X,Y~p(x, y), X, Y的联合熵H(X,Y)定义为　

　　

　　联合熵就是描述一对随机变量平均所需要的信息量

　　给定随机变量X, 随机变量Y的条件熵

　　

　　将联合熵中的log函数展开

　　

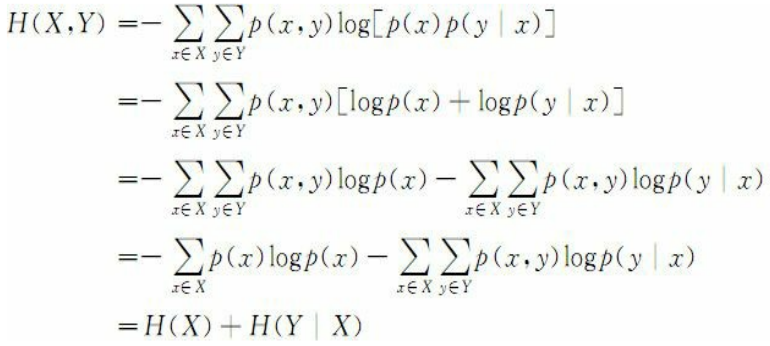
　　将上式称为熵的联合规则, 那么在一般情况下就有

　　

 

 互信息

　　根据熵的连锁规则有

　　

　　可以得到

　　

　　这个差值就叫做X和Y的互信息,记作I(X; Y), 互信息反映的是在知道了Y的值以后X的不确定性的减少量.反之也是一样的.可以理解为Y的值透露了多少关于X的信息量, 具体的如下图所示

　　

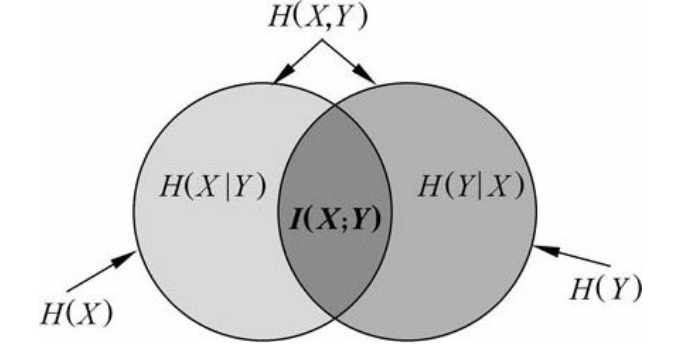
　　对上面的互信息的表达式做一些转换,可以得到

　　

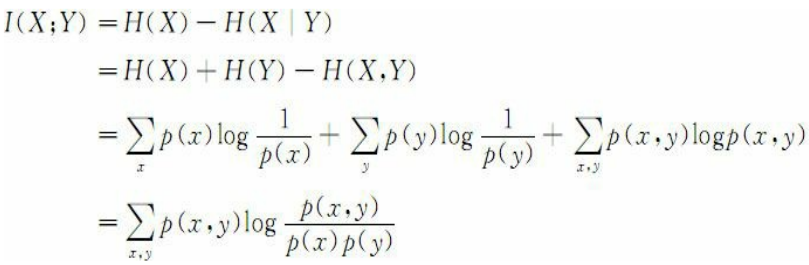
　　由于H(X|X) = 0, 因此

　　

　　这一方面说明了为什么熵又称为自信息,另一方面说明了两个完全相互依赖的变量之间的互信息并不是一个常量,而是取决于它们的熵。实际上, 互信息体现了两个变量之间的依赖程度. 如果I(X;Y)≫0,表明X和Y是高度相关的;如果I(X;Y)=0,表明X和Y是相互独立的;如果I(X;Y)≪0,表明Y的出现不但未使X的不确定性减小,反而增大了X的不确定性,常是不利的。

　　同样,推导条件互信息和互信息的连锁规则

　　

 

相对熵

　　相对熵是衡量相同时间空间里的两个概率分布相对差距的测度. 两个概率分布p(x) 与 q(x)的相对熵定义如下

　　

　　当两个分布差异很小时,相对熵也很小; 当两个分布差异很大时,相对熵也很大

　　互信息实际上就是衡量一个联合分布与独立性差距多大的测度

　　

 

交叉熵

　　交叉熵的概念是用来衡量估计模型与真是概率分布之间的差异情况

　　如果一个随机变量X服从p(x), q(x)为用于近似p(x)的概率分布,那么则有随机变量X与模型q之间的交叉熵为

　　

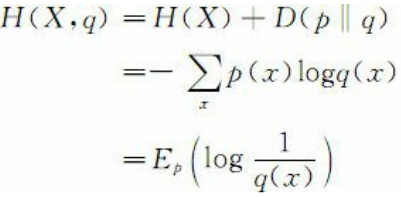
　　很多时候将交叉熵作为损失函数来衡量模型的好坏,交叉熵越小,模型的表现越好