神经网络中的权值初始化方法
1,概述
神经网络中的权值初始化方法有很多,但是这些方法的设计也是遵循一些逻辑的,并且也有自己的适用场景。首先我们假定输入的每个特征是服从均值为0,方差为1的分布(一般输入到神经网络的数据都是要做归一化的,就是为了达到这个条件)。
为了使网络中的信息更好的传递,每一层的特征的方差应该尽可能相等,如果保证这个特征的方差是相等的呢。我们可以从初始化的权重值入手。
首先来做一个公式推导:
$var(s) = var(\sum_i^n w_i x_i)$
$var(s) = \sum_i^n var(w_i x_i)$
$var(s) = \sum_i^n E(w_i^2) E(x_i^2) - (E(x_i))^2 (E(w_i))^2$
$var(s) = \sum_i^n (E(w_i))^2 var(x_i) + (E(x_i))^2 var(w_i) + var(x_i) var(w_i)$
在这里假定了x的均值为0,对于初始化的权重通常均值也是选择0,因此上面的式子可以转换成
$var(s) = \sum_i^n var(x_i) var(w_i)$
又因为x中每个特征我们都假定方差为1,因此上面的式子可以改写成
$var(s) = n * var(w)$
现在要使得$var(s) = 1$,则有
$n * var(w) = 1$。
$var(w) = \frac{1}{n}$。
为了确保量纲和期望一致,我们将方差转换成标准差,因此要确保标准差为$\frac{1}{\sqrt{n}}$
2,初始化方法
现在我们来看看每种方法初始化时我们该如何设置方差能保证输入的分布状态不变。
1)均匀分布
对于均匀分布$U (a, b)$,其期望和方差分别为$E(x) = \frac{(a+b)}{2}, D(x) = \frac{(b-a)^2}{12}$。
假定均匀分布为$(-\frac{1}{\sqrt{d}},\frac{1}{\sqrt{d}})$,在这里$d$为神经元的个数,则有期望和方差为:
$E(x) = 0, D(x) = \frac{1}{3d}$
代入到$var(s) = n * var(w)$中,可以得到:
$var(s) = \frac{1}{3}$,因此为了保证最终的方差为1,因此方差需要乘以3,标准差则需要乘以$\sqrt{3}$。因此一般均匀分布的初始化值可以选择$(-\sqrt{\frac{3}{d}},\sqrt{\frac{3}{d}})$。
在xavier uniform init(glorot uniform),也就是 tf.glorot_uniform_initializer()方法中初始化值为$(-\sqrt{\frac{6}{(d_{in}+d_{out})}},\sqrt{\frac{6}{d_{in}+d_{out}}})$。在一个二维矩阵中$d_{in}, d_{out}$分别表示矩阵的第一个维度和第二个维度。
见下面一个例子,对于tf.glorot_uniform_initializer()方法:

可以看到经过一层神经网络之后,x的期望和方差基本不变。对于均匀分布tf.random_uniform_initializer(),当我们将参数初始化为$(-\sqrt{\frac{3}{d}},\sqrt{\frac{3}{d}})$。其结果如下:

2)正态分布
正态分布会直接给出期望和标准差,所以这个不用多说。为了保证$var(s) = 1$,我们需要让$var(w) = \frac{1}{d}$,则标准差为$\sqrt{\frac{1}{d}}$。
tf.random_normal_initializer(),我们将其标准差设置为$\sqrt{\frac{1}{d}}$。结果如下:

xavier normal init(glorot normal),也就是tf.glorot_normal_initializer(),其标准差为$\sqrt{\frac{2}{(d_{in} + d_{out})}}$,其结果如下:

3)常数初始化
常数初始化时期望为常数值n,方差为0。
tf.zeros_initializer(),以0初始化会导致输出x为0。

tf.ones_initializer(),以1初始化方差会很大

tf.constant_initializer(),同上

3,引入激活函数
上面都是在线性运算的情况下的结果,但实际应用中都是要引入激活函数的,这样神经网络才具有更强的表达能力。如果引入激活函数会怎么样?
为了观看效果,我们将网络层数设置为100层,权重初始化采用tf.glorot_normal_initializer()。
不加激活函数时:

可以看到不加激活函数,方差即使在100层时也基本保持不变。
引入tanh函数,

结果如上,方差会减小到0.005,因此在深层网络中引入归一化层确实是很重要的。
引入relu函数:
上面的结果很显然relu函数并不适用tf.glorot_normal_initializer()。对于relu激活函数时,正态分布的标准差通常为$\sqrt{\frac{2}{d}}$,均匀分布通常为$(-\sqrt{\frac{6}{d}},\sqrt{\frac{6}{d}})$。因此更换下初始化参数,结果如下
上面看结果就好很多了,方差在100层的输出为0.1,结果是比tanh要好的,此外这里的期望不再接近0,因为relu函数就是不像tanh那样关于0对称的。
另外我还发现一个奇怪的事情,暂时无法解释,可以给大家看下结果:
当我们直接用tf.random_normal_initializer()初始化时,此时方差为1。
不引入激活函数。

100层后得到的期望和方差都为nan,应该是发生爆炸了。
引入tanh函数:

100层后竟然能保持方差为1。
relu激活函数:

期望和方差均为0。
从上面的结果看好像在用tanh做激活函数时,可以直接将参数用0,1的正态分布初始化。
4,初始化的随机性
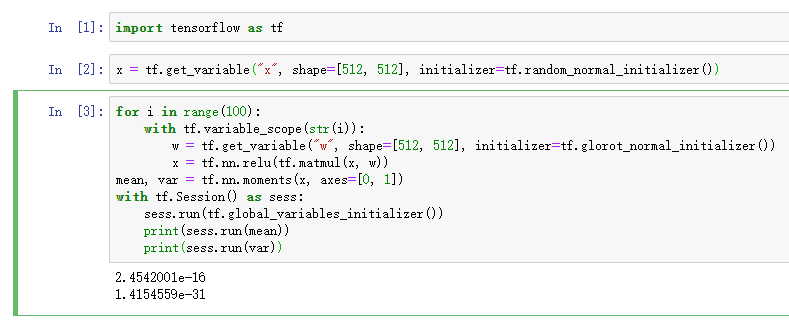
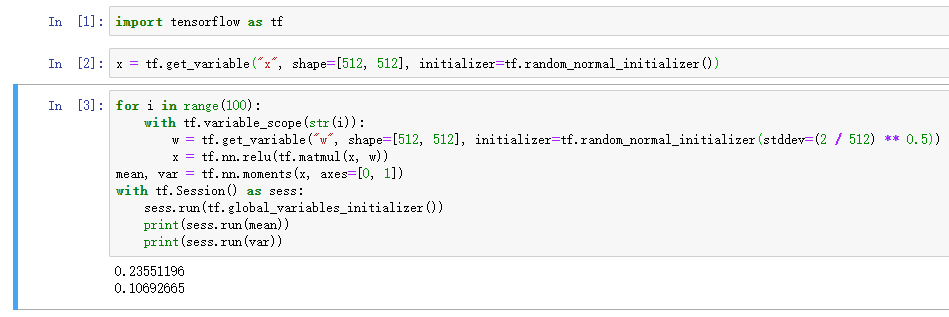
在实践中还发现一个问题,就是参数的大小也会影响最终的结果,以relu激活函数为例。为了方便计算,x和w的维度一致
所有维度为512,两次得到的结果差异比较大:


其实这个也好理解,本身x和w都是随机初始化的,虽然分布是一样的,但是具体的值并不一样,最终的结果也不一样,所以说即使同样的分布初始化,有时候得到的结果也会有所差异,这个差异可能是收敛的速度,也可能是最终的结果等等。
参考文献:




