机器翻译评价指标 — BLEU算法

1，概述

　　机器翻译中常用的自动评价指标是 $BLEU$ 算法，除了在机器翻译中的应用，在其他的 $seq2seq$ 任务中也会使用，例如对话系统。

 

2 $BLEU$算法详解

　　假定人工给出的译文为$reference$，机器翻译的译文为$candidate$。

　　1）最早的$BLEU$算法

　　　　最早的$BLEU$算法是直接统计$cadinate$中的单词有多少个出现在$reference$中，具体的式子是：

　　　　$BLEU = \frac {出现在reference中的candinate的单词的个数} {cadinate中单词的总数}$

　　　　以下面例子为例：

　　　　$ candinate:$ the the the the the the the 

　　　　$ reference:$ the cat is on the mat 

　　　　$cadinate$中所有的单词都在$reference$中出现过，因此：

　　　　$BLEU = \frac {7} {7} = 1$

　　　　对上面的结果显然是不合理的，而且主要是分子的统计不合理，因此对上面式子中的分子进行了改进。

　　2）改进的$BLEU$算法 — 分子截断计数

　　　　针对上面不合理的结果，对分子的计算进行了改进，具体的做法如下：

　　　　$Count_{w_i}^{clip} = min(Count_{w_i},Ref\_Count_{w_i})$

　　　　上面式子中：

　　　　$Count_{w_i}$ 表示单词$w_i$在$candinate$中出现的次数；

　　　　$Ref\_Count_{w_i}$ 表示单词$w_i$在$reference$中出现的次数；

　　　　但一般情况下$reference$可能会有多个，因此有：

　　　　$Count^{clip} = max(Count_{w_i,j}^{clip}), j=1,2,3......$

　　　　上面式子中：$j$表示第$j$个$reference$。

　　　　仍然以上面的例子为例，在$candinate$中只有一个单词$the$，因此只要计算一个$Count^{clip}$，$the$在$reference$中只出现了两次，因此：

　　　　$BLEU = \frac {2} {7}$

　　3）引入$n-gram$

　　　　在上面我们一直谈的都是对于单个单词进行计算，单个单词可以看作时$1-gram$，$1-gram$可以描述翻译的充分性，即逐字翻译的能力，但不能关注翻译的流畅性，因此引入了$n-gram$，在这里一般$n$不大于4。引入$n-gram$后的表达式如下：

　　　　$p_{n}=\frac{\sum_{c_{\in candidates}}\sum_{n-gram_{\in c}}Count_{clip}(n-gram)}{\sum_{c^{'}_{\in candidates}}\sum_{n-gram^{'}_{\in c^{'}}}Count(n-gram^{'})}$

　　　　很多时候在评价一个系统时会用多条$candinate$来评价，因此上面式子中引入了一个候选集合$candinates$。$p_{n}$ 中的$n$表示$n-gram$，$p_{n}$表示$n_gram$的精度，即$1-gram$时，$n = 1$。

　　　　接下来简单的理解下上面的式子，首先来看分子：

　　　　1）第一个$\sum$ 描述的是各个$candinate$的总和；

　　　　2）第二个$\sum$ 描述的是一条$candinate$中所有的$n-gram$的总和；

　　　　3）$Count_{clip}(n-gram)$ 表示某一个$n-gram$词的截断计数；

　　　　再来看分母，前两个$\sum$和分子中的含义一样，$Count(n-gram^{'})$表示$n-gram^{'}$在$candinate$中的计数。

　　　　再进一步来看，实际上分母就是$candinate$中$n-gram$的个数，分子是出现在$reference$中的$candinate$中$n-gram$的个数。

　　　　举一个例子来看看实际的计算：

　　　　$candinate:$ the cat sat on the mat

　　　　$reference:$ the cat is on the mat

　　　　计算$n-gram$的精度：

　　　　$p_1 = \frac {5} {6} = 0.83333$

　　　　$p_2 = \frac {3} {5} = 0.6$

　　　　$p_3 = \frac {1} {4} = 0.25$

　　　　$p_4 = \frac {0} {3} = 0$

　　4）添加对句子长度的乘法因子

　　　　在翻译时，若出现译文很短的句子时往往会有较高的$BLEU$值，因此引入对句子长度的乘法因子，其表达式如下：

　　　　

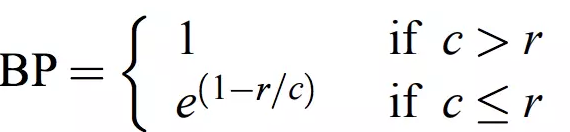
　　　　在这里$c$表示$cadinate$的长度，$r$表示$reference$的长度。

　　将上面的整合在一起，得到最终的表达式：

　　　　$BLEU = BP exp(\sum_{n=1}^N w_n \log p_n)$

　　其中$exp(\sum_{n=1}^N w_n \log p_n)$ 表示不同的$n-gram$的精度的对数的加权和。

 

3，$NLTK$实现

　　可以直接用工具包实现

from nltk.translate.bleu_score import sentence_bleu, corpus_bleu
from nltk.translate.bleu_score import SmoothingFunction
reference = [['The', 'cat', 'is', 'on', 'the', 'mat']]
candidate = ['The', 'cat', 'sat', 'on', 'the', 'mat']
smooth = SmoothingFunction()  # 定义平滑函数对象
score = sentence_bleu(reference, candidate, weight=(0.25,0.25, 0.25, 0.25), smoothing_function=smooth.method1)
corpus_score = corpus_bleu([reference], [candidate], smoothing_function=smooth.method1)

　　$NLTK$中提供了两种计算$BLEU$的方法，实际上在sentence_bleu中是调用了corpus_bleu方法，另外要注意$reference$和$candinate$连个参数的列表嵌套不要错了，weight参数是设置不同的$n-gram$的权重，另外weight元祖中的数量决定了计算$BLEU$时，会用几个$n-gram$，以上面为例，会用$1-gram, 2-gram, 3-gram, 4-gram$。SmoothingFunction是用来平滑log函数的结果的，防止$f_n = 0$时，取对数为负无穷。