数据结构之非线性结构

非线性结构

树

树的定义

我们可以简单的认为：

• 树有且仅有一个根节点
• 有若干个互不相交的子树，这些子树本身也是一颗树

通俗的定义：
1.树就是由节点和边组成的
2.每一个节点只能有一个父节点，但可以有多个子节点。但有一个节点例外，该节点没有父节点，此节点就称为根节点

树的专业术语

• 节点
• 父节点
• 子节点
• 子孙
• 堂兄弟
• 兄弟
• 深度
  • 从根节点到最底层节点的层数被称为深度，根节点是第一层
• 叶子节点
  • 没有子节点的节点
• 度
  • 子节点的个数

树的分类

• 一般树
  • 任意一个节点的子节点的个数不受限制
• 二叉树
  • 定义：任意一个节点的子节点的个数最多是两个，且子节点的位置不可更改
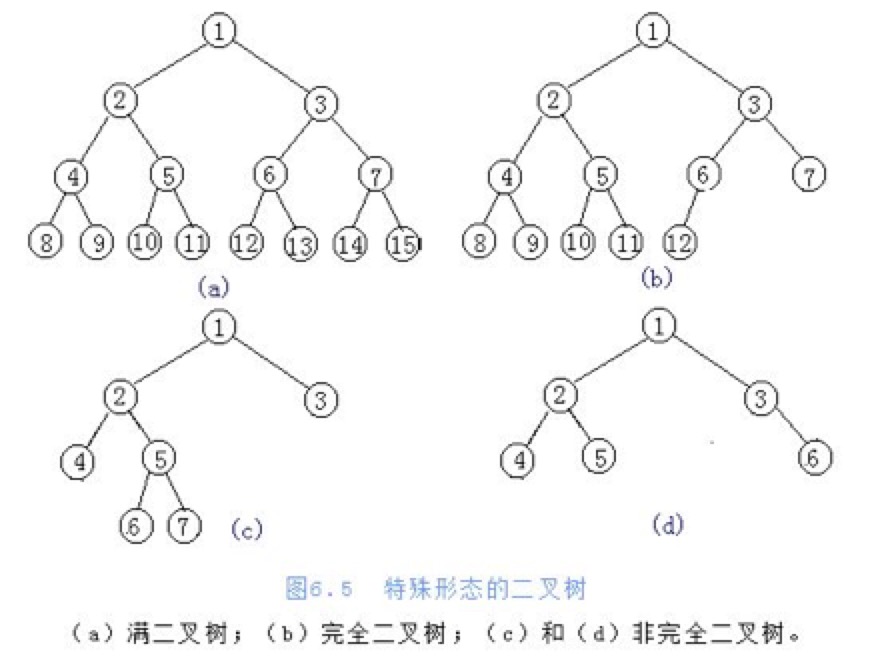
    • 满二叉树
      • 定义：在不增加层数的前提下，无法再多添加一个节点的二叉树
    • 完全二叉树
      • 定义：只是删除了满二叉树最底层最右边连续的若干个节点
    • 一般二叉树
• 森林
  • n个互不相交的数的集合

树的操作(伪算法)

如何把一个非线性结构的数据转换成一个线性结构的数据存储起来？

• 一般树的存储
  • 双亲表示法
    • 求父节点方便
  • 孩子表示法
    • 求子节点方便
  • 双亲孩子表示法
    • 求父节点和子节点都很方便
  • 二叉树表示法
    • 即把一般树转换成二叉树，按照二叉树的方式进行存储
    • 具体的转化办法：
      • 设法保证任意一个节点的：
        • 左指针域指向它的第一个孩子
        • 右指针域指向它的下一个兄弟
      • 只要能满足上述的条件就能够转化成功

• 二叉树的操作

  • 连续存储 （完全二叉树，数组方式进行存储）
    • 优点：查找某个节点的父节点和子节点非常的快
    • 缺点：耗用内存空间过大
    • 转化的方法：先序 中序 后序
  • 链式存储 （链表存储）
    • data区域 左孩子区域 右孩子区域

• 森林的操作

  • 把所有的树转化成二叉树，方法同一般树的转化

二叉树具体的操作

1.二叉树的先序遍历[先访问根节点]

• 先访问根节点
• 再先序遍历左子树
• 再先序遍历右子树

2.二叉树的中序遍历 [中间访问根节点]

• 先中序遍历左子树
• 再访问根节点
• 再中序遍历右子树

3.二叉树的后序遍历 [最后访问根节点]

• 先中序遍历左子树
• 再中序遍历右子树
• 再访问根节点

4.已知先序和中序，如何求出后序？

1 2 3 4 5 6 7 8 9 10 11 12 13

#### 例一 先序：ABCDEFGH 中序：BDCEAFHG   求后序？ 后序：DECBHGFA   #### 例二 先序：ABDGHCEFI 中序：GDHBAECIF   求后序？ 后序：GHDBEIFCA

5.已知中序和后序，如何求出先序？

1 2 3 4 5

中序：BDCEAFHG 后序：DECBHGFA   求先序？ 先序：ABCDEFGH

点击显/隐

树的应用

• 树是数据库中数据组织的一种重要形式
• 操作系统子父进程的关系本身就是一颗树
• 面型对象语言中类的继承关系